加速度计的数据解读
来源:http://www.cnblogs.com/wb-DarkHorse/p/3173666.html
一:加速度计介绍
加速度计是用来测试线性加速度的一种传感器,相对于电子陀螺仪,它具有长时间稳定的特点。但因为受到重力的影响,短时间内会有噪声。关于加速度计的原理和结构,可以参考我CSDN上转载的一篇文章:http://blog.csdn.net/lovewubo/article/details/9084291
里面的内容很详细。本文只对从加速度计得到的数据进行解读。数据是从国外的一个大牛博客那里得到的(那人貌似是叫SOH Madgwick),那篇博文讲解了一种融合加速度计和陀螺仪的姿态解算算法,这里不讨论。只是把里面的一份加速度计的数据抽取出来,分析一下为什么加速度计的读数会是那个样子。
首先说明一下,那位大牛的实验中,把传感器设备分别围绕三个轴旋转正90度,回到起始位置,再反向旋转90度,回到起始位置。三个轴的方向是这样定义的:
二:加速度计的输出分析
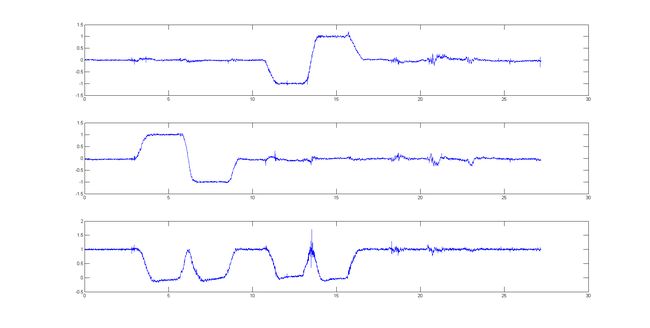
我们对加速度计三个轴的输出进行了描述:
从上到下,依次是X,Y,Z三个轴上的加速度数据。让我们分析一下,为什么会产生这样的输出。首先看这个图:
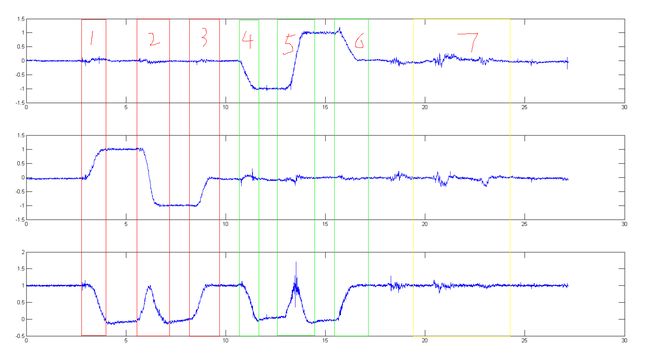
我将图中用三种颜色标识了三个区域,矩形框1-3标识区域1,2-6标识区域2,7标识区域3。ok,现在开始。
其实这三个区域分别代表了三次绕不同轴旋转的过程。第一个是绕X轴正负旋转90度,第二个对应Y轴旋转,第三个对应Z轴旋转。下面逐一分析,首先看区域1,它的三个矩形分别代表了这样三个子过程:
1 绕X轴旋转90度
解释如下:当绕X轴旋转90度时,Y轴慢慢向上翘,Z轴慢慢向下靠(我擦,蛮押韵的)。当完全达到90度时,由于Y轴与重力方向刚好相反,所以Y轴的输出是1g(1g==9.8m/s^2),而Z轴的值从原来的1逐渐减小为0。这个状态估计保持了1秒钟吧,对应矩形1和2之间的平坦区域
2 回到初始位置,并反向旋转90度
解释如下:接着当回到初始位置时,Y轴数据慢慢减小为0,而Z轴数据慢慢上升为1。然后逆向旋转90度,Y轴慢慢减小,直至为-1,因为此时Y轴方向与重力方向一致了,而反应出来的加速度值应该是负值。而Z轴慢慢减小为0
3 回到初始位置
解释如下:然后从逆向90度回到初始位置。此时Y轴和Z轴的数据慢慢恢复到初始值,Y轴为0,而Z轴为1
分析完了X轴的旋转,其实Y轴的旋转也是类似的,就不说了。现在说说Z轴的,因为绕Z轴旋转时,相当于左右摆动90度,此时Z轴的输出始终是1,而X轴和Y轴由于是正交于重力轴的,所以输出值都是0,当然这都是在相对静止的条件下的值。如果是将这个设备安装在车辆上,当车左右转弯时,X轴和Y轴的读数可不一定是0,因为这两个方向会受到车辆速度冲击力的影响,这就是加速度引起的惯性力,正是借助与这个惯性力,加速度计才能测量加速度。而自然界的重力成为影响传感器的噪声来源,而如何消除这些噪声,就是另外要考虑的滤波算法了。正如那位国外大牛的文章,可以用陀螺仪进行矫正。也可以参考本文最开始的CSDN上的那个链接里面讲到的融合算法,当然也可以考虑用卡尔曼滤波,以后慢慢研究。
三:计算倾斜角
先上图:
我们感兴趣的角度是向量R和X,Y,Z轴之间的夹角,那就令这些角度为Axr,Ayr,Azr。观察由R和Rx组成的直角三角形:
cos(Axr) = Rx / R
cos(Ayr) = Ry / R
cos(Azr) = Rz / R
其中,R = SQRT( Rx^2 + Ry^2 + Rz^2)
通过arccos()函数(cos()的反函数)我们可以计算出所需的角度:
Axr = arccos(Rx/R)
Ayr = arccos(Ry/R)
Azr = arccos(Rz/R)
matlab代码:
function AcceCalDegree
%%加速度计计算角度,这个角度是传感器三个坐标轴的倾斜角
%%%%%%%%%%%%%%%%%%%%%%%
clc;
clear;
load('ExampleData.mat');
nCount = length(time);
Degree = zeros(nCount,3);
for i=1:nCount
[Degree(i,1) Degree(i,2) Degree(i,3)] = GetDegreeFromAcce(Accelerometer(i,1), Accelerometer(i,2), Accelerometer(i,3));
end
figure(1);
subplot(3,1,1);plot(time, Degree(:,1));title('x轴的倾斜角度');
subplot(3,1,2);plot(time, Degree(:,2));title('y轴的倾斜角度');
subplot(3,1,3);plot(time, Degree(:,3));title('z轴的倾斜角度');
function [dx dy dz] = GetDegreeFromAcce(ax, ay, az)
%%%ax ay az代表加速度计的三个轴的读数
%%%dxy dxz dyz分别代表在三个平面内的角度,即旋转角度
R = sqrt(ax^2 + ay^2 + az^2);
%%计算角度
dx = acos(ax/R) * 180 / pi;
dy = acos(ay/R) * 180 / pi;
dz = acos(az/R) * 180 / pi; %将弧度转换为角度
从上图中,可以直观的看到,绕不同的轴旋转是,重力方向与三个轴的角度变化。