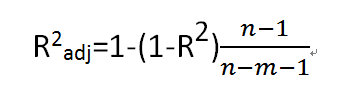数据挖掘方法(4):多元回归
一. 概述
前面介绍了一个预测变量和一个回应变量的回归,但数据挖掘通常对一个回应变量和多个预测变量之间的关系更感兴趣,数据中可能有很多变量都与目标(回应)变量有线性关系,多元回归模型可以更加精确的预测这些关联。
多元回归模型如下:
y=b0+b1*x1+b2*x2+.......+e
其中b0,b1,b2.....是模型参数,为常数,可以通过最小二乘法估计。关于误差项e和回应变量y的假设与简单线性回归模型一样。
二 多元回归的推断
主要有:
(1)t检验,用来对预测变量xi和回应变量y之间的关系进行推断
(2)F检验,用来对整个回归模型的显著性进行检验
(3)bi,第i个预测变量系数的置信区间
(4)回应变量y的均值的置信区间,用于预测变量x1,x2,x3,...取特定值时,对回应变量y的均值进行估计。
2.1 y和xi之间关系的t检验
假设检验如下:
. H0: bi=0
.H1: bi!=0
这些假设的模型的唯一区别是第i项是否存在,其他项都是相同的。
实例: 营养级别和糖之间关系的t检验
.H0: b1=0; 模型: y=b0+b2(纤维)+e
.H1:b1!=0; 模型: y=b0+b1(糖)+b2(纤维)+e
还是使用数据集:谷物(在本系列文章第二篇中有下载地址:谷物)
>#数据集存储在sugar中
>#线性拟合
> mutil_regre<-lm(data=sugar,rating~sugars+fiber)
>#查看
> summary(mutil_regre)
Call:
lm(formula = rating ~ sugars + fiber, data = sugar)
Residuals:
Min 1Q Median 3Q Max
-12.133 -4.247 -1.031 2.620 16.398
Coefficients:
Estimate Std. Error t value
(Intercept) 51.6097 1.5463 33.376
sugars -2.1837 0.1621 -13.470
fiber 2.8679 0.3023 9.486
Pr(>|t|)
(Intercept) < 2e-16 ***
sugars < 2e-16 ***
fiber 2.02e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.219 on 74 degrees of freedom
Multiple R-squared: 0.8092, Adjusted R-squared: 0.804
F-statistic: 156.9 on 2 and 74 DF, p-value: < 2.2e-16
可以得到,糖对应的系数为 b
1
=-2.1837,对应的标准差为:S
b
1
=0.1621
T对应的t统计量,也即检验的统计量为: t=b1/Sb1=-2.1837/0.1621=-13.4713
P值对应的是t统计量的p值。也即: p=P(|t|>tobs)=P(|t|>-13.4713)约等于0. 使用p值来检验假设,当p值很小时就可以拒绝原假设。
2.2 整体回归模型的显著性水平检验:F检验
t检验是分别对每个变量,糖,纤维,....逐个检验与回应变量线性关系。即{营养级别|糖},{营养级别|纤维},...
F检验是对所有变量一起检测与回应变量关系,即{营养级别|糖,纤维,......}
F检验的前提是:
.H0: b0=b1=......=0 也即模型为:y=b0+e
.H1:至少存在一个bi不等于零
备选假设H1并不要求任何回归系数都不是零,而是当备选假设为真时,存在一个回归系数不是零。因此,F检验的备选假设并没有唯一确定一个模型,当一个、几个或者所有回归系数都不是零时,备选假设都是成立的。
F统计量为:
F=Fobs=MSR/MSE ,服从Fm,n-m-1分布
如何理解:MSE(误差平方和均值)能很好的估计总体变异σ^2(不论原假设是否为真),而MSR只有当原假设为真时才是σ^2的优良统计量,因而只有在原假设为真的情况下MSR和MSE才会比较接近,也即F很小的时候,有足够的争取表明原假设为真。
>#查看方差分析表
>anova(mutil_regre)
Analysis of Variance Table
Response: rating
Df Sum Sq Mean Sq F value Pr(>F)
sugars 1 8654.7 8654.7 223.774 < 2.2e-16 ***
fiber 1 3480.0 3480.0 89.978 2.023e-14 ***
Residuals 74 2862.0 38.7
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 注意:方差分析表只给出了均方误差(MSE=Mean Sq=38.7) 而第一步中t检验中查看线性拟合时已经直接给出了F统计量:
F-statistic: 156.9 on 2 and 74 DF, p-value: < 2.2e-16
其中的p值小于任何合理的显著性水平所要求的值,因而拒绝原假设。
2.3 特定回归系数的置信区间
可以为某个回归系数构造一个 100(1-a)%的置信区间,与简单线性回归无异。
2.4 给定x1,x2,x3,....下,y均值的置信区间
与简单线性回归类似,只不过变量增多。变为如:谷物为5.00克的糖和5.00克纤维时,营养级别的均值分布。。
3. 三个参数
3.1 调整R^2 :对包含无用预测变量的惩罚模式
3.2 序贯的误差平方和(sequential sums of squares)
| 来源 | DF | Seq SS |
| 糖 | 1 | 8701.7 |
| 纤维 | 1 | 3416.1 |
| 货架1 | 1 | 0.3 |
| 货架2 | 1 | 152.4 |
3.3 偏F检验
假设模型中已经有了p个变量,x1,x2,x3,....xp,一个新的变量x*是否应该包含在此模型中?应该计算将x*加入到给定含有p个变量的模型中所产生的额外序列平方和,这个值表示为: SSextra=SS(x*|x1,x2,x3,....xp)。现在,额外序列平方和通过在全模型(包括x1,x2,x3,....xp和x*)中的回归平方和计算得到,表示为SSfull=SS(x1,x2,x3,....xp,x*),从全模型的回归平方和中减速缩减模型(仅包含x1,x2,x3,....xp)的回归平方和(表示为:SSreduced=SS(x1,x2,x3,....xp)),也即:
SSextra=SSfull-SSreduced
即:
SS(x*|x1,x2,x3,....xp)=SS(x1,x2,x3,....xp,x*)-SS(x1,x2,x3,....xp)
偏F检验的原假设如下:
.H0:否定SSextra与x*是相关的,对已经包含x1,x2,x3,....xp的模型的回归平方和没有显著的共享。因此,模型中不应该包含x*。
.H1:肯定SSextra与x*是相关的,对已经包含x1,x2,x3,....xp的模型的回归平方和有显著的贡献。因此,模型中应该包含x*
偏F检验的测试统计量是F(x*|x1,x2,x3,....xp)=SSextra/MSEfull。MSEfull代表全模型的均方误差,包括x1,x2,x3,....xp和x*。当假设为真时,这个统计量服从F1,n-p-2的分布。因此,当F(x*|x1,x2,x3,....xp)值太大或者它像对应的p值太小时,有理由拒绝原假设。而偏F检验的一个可替代的方法是t检验。一个自由度为1和n-p-2的F检验等价于一个自由度为n-p-2的t检验。这是由他们之间的概率分布关系(F1,n-p-2=(tn-p-2)^2).
注意:序贯平方和与部分平方和的区别如下: