面试算法题:忘我之乘积分析
题目:给你一个数组A[1..n],请你在O(n)的时间里构造一个新的数组B[1..n],使得B[i]=A[1]*A[2]*...*A[n]/A[i]。你不能使用除法运算。
分析:要求在不使用除法的情况下计算B[i]=A[1]*A[2]*...*A[n]/A[i],变换一个公式得到B[i]=A[1]*A[2]*A[3]*...*A[i-1]*A[i+1]*...*A[n],一共n-1次乘法。每一个B[i]计算一遍,总的时间复杂度为O(n^2)。不符合题目的要求,当然如果是用并行的方法的话,那么用n个核,每一个核i(1<=i<=n)去处理计算B[i],同样时间复杂度是O(n),但是如果是单核上设计,那么必须减少乘法的次数。
B[i]可以通过两个部分得到:
一.A[1]*...*A[i-1] ;
二.A[i+1]*...*A[n]。
第一部分,在计算B[i+1]的时候,是可以用B[i]的第一部分的结果的,只需要乘以A[i]即得B[i+1]的第一部分。
第二部分同理,计算完A[i+1]*...*A[n],再计算A[i]*A[i+1]*...*A[n],只需要乘以A[i]即可。
由此分析,构建两个新的数组C和D:
C[i]=A[1]*A[2]*...*A[i-2]*A[i-1]=C[i-1]*A[i-1]
D[i]=A[i+1]*A[i+2]*...*A[n]=A[i+1]*D[i+1]
构建C和D都是O(n) 的时间复杂度(C从前到后遍历一遍数组,D从后向前遍历一边数组),然后B[i]=C[i]*D[i]也是O(n)的时间复杂度。整体算法的时间复杂度是:O(n)。空间复杂度是:O(n)。实际上是通过提高空间复杂度来降低时间复杂度。
The Code:
#include<iostream>
#include<stdio.h>
using namespace std;
int A[]={0,1,2,3,4,5,6,7,8,9,10,11};
int B[20],C[20],D[20];
int main()
{
int i;
/*计算数组C*/
C[1]=1;
for(i=2;i<=11;i++)/*下标从1开始*/
C[i]=C[i-1]*A[i-1];
for(i=1;i<=11;i++)
printf("C[%d] = %d\n",i,C[i]);
/*计算数组D*/
D[11]=1;
for(i=10;i>=1;i--)
D[i]=D[i+1]*A[i+1];
for(i=1;i<=11;i++)
printf("D[%d] = %d\n",i,D[i]);
/*计算B[i]=D[i]*C[i]*/
for(i=1;i<=11;i++)
B[i]=C[i]*D[i];
for(i=1;i<=11;i++)
printf("B[%d] = %d\n",i,B[i]);
return 0 ;
}
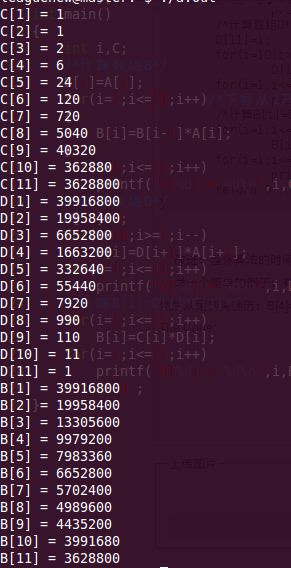
运行结果:
改进:整体算法的时间复杂度是:O(n)。空间复杂度是:O(1)。
举一个简单的例子:有5个数的数组A[1],A[2],A[3],A[4],A[5]。
首先从头到尾遍历:B[1]=A[1] ; B[2]=B[1]*A[2] ; B[3]=B[2]*A[3] ; B[4]=B[3]*A[4] ; B[5]=B[4] ; 临时变量 C=A[5]。
然后从尾到头遍历:B[4]=B[3]*C , C=C*A[4] ; B[3]=B[2]*C , C=C*A[3] ; B[2]=B[1]*C , C=C*A[2] ; B[1]=C。这个算法中临时变量C的作用类似与上一个算法中的数组D的作用。
The Code:
#include<iostream>
#include<stdio.h>
using namespace std;
int A[]={0,1,2,3,4,5,6,7,8,9,10,11};
int B[20];
int main()
{
int i,C;
/*计算数组B*/
B[1]=A[1];
for(i=2;i<=10;i++)/*下标从1开始*/
{
B[i]=B[i-1]*A[i];
}
B[11]=B[10];
C=A[11];
for(i=10;i>=1;i--)
{
B[i]=B[i-1]*C;
C*=A[i];
}
B[1]=C;
for(i=1;i<=11;i++)
printf("B[%d] = %d\n",i,B[i]);
return 0 ;
}
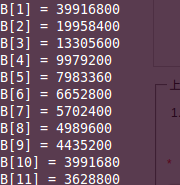
运行结果:
转载情注明出处:http://blog.csdn.net/lavorange/article/details/9255649