约瑟夫问题的笨方法求解程序

据说著名犹太历史学家 Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从，Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

17世纪法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事：15个教徒和15个非教徒在深海上遇险，必须将一半的人投入海中，其余的人才能幸免于难，于是想了一个办法：30个人围成一圆圈，从第一个人开始依次报数，每数到第九个人就将他扔入大海，如此循环进行直到仅余15个人为止。问怎样排法，才能使每次投入大海的都是非教徒。

上述两个例子都可以归结为--约瑟夫问题：N个人围成一圈，从第一个开始报数，第M个将被杀掉，最后剩下Q个。围成一圈就启发我们用循环链表来解决该问题，本文使用结构数组来构成一个循环链。结构数组中有两个成员：指向下一个成员的指针和是否在圈圈里的标志。

先给出30个人在海上去留问题的解决代码，再给出一般问题的代码，代码中有相关注释（代码均经过调试，结果正确）。关于约瑟夫问题的数学解法和优化算法暂时没有研究，以后研究后再编辑上：

/*
解决问题：30个人在海上，通过数数决定被抛到海里的人，数到9的被抛入海中，最终剩下15个人。
时间：2012.9.9
作者：赵雨
*/
#include "stdafx.h"
#include<iostream>
#include<stdio.h>

using namespace std;

struct node {
	int next;		//指向数组的下一个下标，下标即编号
	int out;		//1表示没有被扔下海；0表示被扔下海
}link[31];

int _tmain(int argc, _TCHAR* argv[])
{
	int i, j, k;

	for(i=1; i<=30; i++) {		//节点元素赋初值，30个人全部在船上，指向下一个元素
		link[i].next = i+1;
		link[i].out =1;
	}
	link[30].next = 1;		//最后一个人，指向第一个人，从而用循环链来表示环的形状
	j = 1;		//j的初值1,表示船上人员的编号
	for( i=0; i<15; i++) {
		for( k=0;k<9 ; ) {			
			k += link[j].out;		//开始数数
			if( k == 9)  {
				link[j].out = 0;   //当数到9的时候，将这个抛到海中，置为1
				cout<<"第"<<i+1<<"个被抛入海中的是编号为"<<j<<"的人"<<endl;
			}
			j= link[j].next;	//到下一个人
		}			
	}
	cout<<endl;
	cout<<"@表示在船上，+表示被扔下海，编号从1到30的状态依次可以表示为："<<endl;

	for( i=1; i<=30; i++) 
		cout<<" "<< (link[i].out?'@':'+');   //<<的优先级高于条件操作符，故需要括号。
	
	cout<<endl;
	return 0;
}

运行结果为：

将该程序推广到一般问题的代码如下：

#include "stdafx.h"
#include<iostream>
#include<stdio.h>

using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
	int i, j, k;
	int N,M,Q;
	cout<<"please input the totol number of people: ";
	cin>>N;

	if(N>100)
		cout<<"请输入不大于100的人数！"<<endl;
	cout<<"please input the count_number of the list: ";
	cin>>M;
	cout<<"please input the number staying in the list: ";
	cin>>Q;

	struct node {
		int next;		//指向数组的下一个下标，下标即编号
		int out;		
	}link[100];

	for(i=1; i<=N; i++) {		
		link[i].next = i+1;
		link[i].out =1;
	}
	link[N].next = 1;		//最后一个人，指向第一个人，从而用循环链来表示环的形状
	j = 1;		//j的初值1,表示船上人员的编号
	for( i=0; i<Q; i++) {
		for( k=0;k<M ; ) {			
			k += link[j].out;		//开始数数
			if( k == M)  {
				link[j].out = 0;   
				cout<<"第"<<i+1<<"个出列的是编号为"<<j<<"的人"<<endl;
			}
			j= link[j].next;	//到下一个人
		}			
	}

	cout<<endl;

	cout<<"@表示在圈圈里，+表示出了圈圈，编号从1到"<<N<<"的状态依次可以表示为："<<endl;

	for( i=1; i<=N;i++) 
		cout<<" "<< (link[i].out?'@':'+');   //注意：<<的优先级高于条件操作符，故需要括号。
	
	cout<<endl;
	return 0;
}

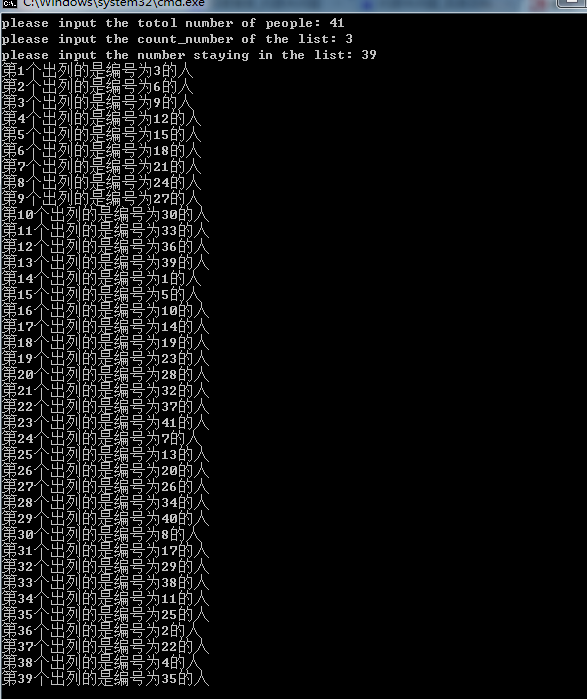
用约瑟夫问题的来源来做测试，运行结果为：

可以看出留在队列中的编号为16和31的两个人。

参考链接：http://blog.csdn.net/yclinuxmyf/article/details/1938112 和百度百科。