支持向量机SVM浅谈

参考文章http://blog.csdn.net/v_july_v/article/details/7624837和http://www.blogjava.net/zhenandaci/archive/2009/02/13/254519.html和http://www.cnblogs.com/scut-fm/p/4194814.html
支持向量机，因其英文名为support vector machine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

在支持向量机中，需要找到一个超平面将给定的数据划分为两类，超平面的方程为，公式的来源可以参考平面方程http://wenku.baidu.com/view/78c4be7c5acfa1c7aa00cc8b.html
在支持向量机模型中，定义函数，通过观察的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。
函数间隔为，g(x)>0,表示分类正确；g(x)<0,表示分类错误。但是像g(x)>0这样的没有等号的开集约束条件，在数学上可能比较难以处理，所以这里将其变换成g(x)>=1这样的包含等号的闭集约束条件。在几何中的含义就是，分别做了两个平行的超平面和这两个超平面与原来的超平面关系如图所示
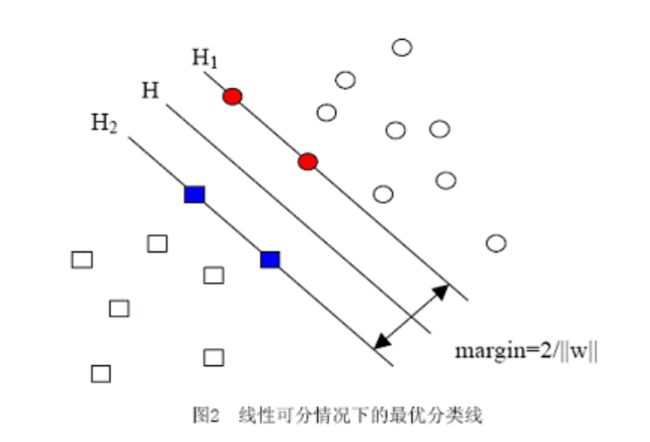
这两个超平面的之间的距离是。这里引出几何间隔的概念，几何间隔所表示的是点到超平面的欧氏距离，同样可以定义一个点的集合（就是一组样本）到某个超平面的距离为此集合中离超平面最近的点的距离。在支持向量机中,对于g(x)>=1的点集可以使用和到超平面的几何距离表示，对于线性可分的训练样本，可以把所有的训练样本都正确分类的解有无数个。这里一般选取能够最充裕地把正样本和负样本进行分离的超平面作为最优解。如图所示，D才是最优解
用数学公式描述即为
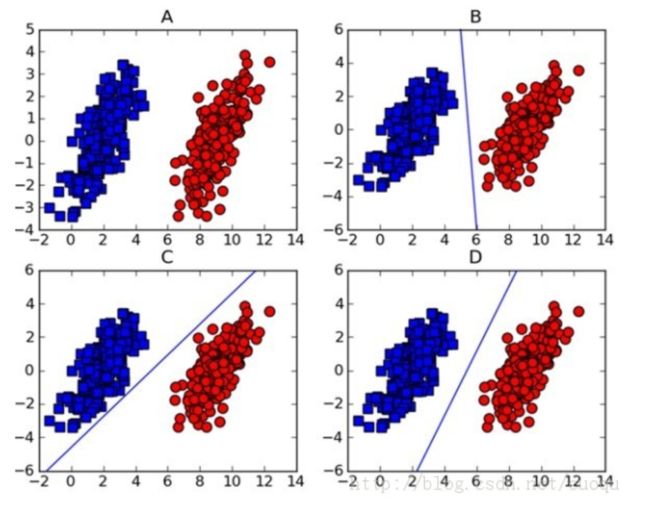
由于求的最大值相当于求的最小值，所以上述目标函数等价于
因为现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。