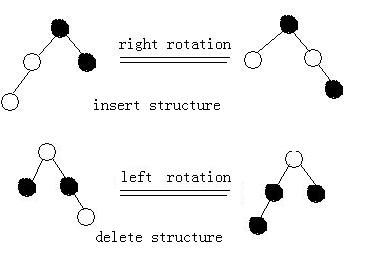
红黑树的删除
删除比插入复杂不少,但深入分析,发现它的关键形状和插入极其类似,记住这个形状!
case1,即sibling 结点为红色,不为黑色,这时需要对其parents结点作一次左旋操作,则此时sibling 结点必为黑色;以下的case2 case3 case4中sibling 结点均为黑色
case2,sibling 结点的两个子结点均为黑色,此时置sibling 结点为红色,然后再以parent 结点为基准重新循环
case3, 互换sibling 及其左子结点颜色(左子结点为红色),然后对sibling 结点作一次右旋操作即转换为case4
case4, 互换sibling 及其父结点颜色,然后对parents结点作一次左旋操作
以下代码完全取自 Linux 内核,刚开始觉得很多地方可以优化,最后发现它是为性能做了最大的优化!
static void rb_delete_color(struct rb_node *node, struct rb_node *parent, struct rb_root *root)
{
struct rb_node *sib;
while ((node == NULL || node->color == RB_BLACK) && node != root->rb_node) {
if (parent->left == node) {
/* case 1, sib is red */
sib = parent->right;
if (sib->color == RB_RED) {
parent->color = RB_RED;
sib->color = RB_BLACK;
__rb_rotate_left(parent, root);
sib = parent->right;
/* goto case 2 */
}
/* case 2, sib is already black, all children of sib is black */
if ((sib->left == NULL || sib->left->color == RB_BLACK)
&& (sib->right == NULL || sib->right->color == RB_BLACK)) {
sib->color = RB_RED;
node = parent;
parent = node->parent;
if (node == root->rb_node)
root->bh--;
continue;
}
/* case 3, sib is already black, right child is black, left child is red */
if (sib->right == NULL || sib->right->color == RB_BLACK) {
sib->color = RB_RED;
sib->left->color = RB_BLACK;
__rb_rotate_right(sib, root);
sib = parent->right;
/* goto case 4 */
}
/* case 4, sib is already black, right child is red */
sib->color = parent->color;
parent->color = RB_BLACK;
if (sib->right)
sib->right->color = RB_BLACK;
__rb_rotate_left(parent, root);
node = root->rb_node;
}
else {
/* case 1, sib is red */
sib = parent->left;
if (sib->color == RB_RED) {
parent->color = RB_RED;
sib->color = RB_BLACK;
__rb_rotate_right(parent, root);
sib = parent->left;
/* goto case 2 */
}
/* case 2, sib is already black, all children of sib is black */
if ((sib->left == NULL || sib->left->color == RB_BLACK)
&& (sib->right == NULL || sib->right->color == RB_BLACK)) {
sib->color = RB_RED;
node = parent;
parent = node->parent;
if (node == root->rb_node)
root->bh--;
continue;
}
/* case 3, sib is already black, left child is black, right child is red */
if (sib->left == NULL || sib->left->color == RB_BLACK) {
sib->color = RB_RED;
sib->right->color = RB_BLACK;
__rb_rotate_left(sib, root);
sib = parent->left;
/* goto case 4 */
}
/* case 4, sib is already black, left child is red */
sib->color = parent->color;
parent->color = RB_BLACK;
if (sib->left)
sib->left->color = RB_BLACK;
__rb_rotate_right(parent, root);
node = root->rb_node;
}
}
if (node) {
node->color = RB_BLACK;
}
}
static void rb_delete(struct rb_node *node, struct rb_root *root)
{
int color;
struct rb_node *child, *parent;
if (node->left == NULL)
child = node->right;
else if (node->right == NULL)
child = node->left;
else { /* use successor instead of node */
struct rb_node *old = node, *left;
node = node->right;
while ((left = node->left) != NULL)
node = left;
child = node->right;
parent = node->parent;
color = node->color;
if (child)
child->parent = parent;
if (old == parent) {/* successor is just the right child of node */
parent->right = child;
parent = node;
}
else
parent->left = child;
/* update successor as old node */
node->parent = old->parent;
node->color = old->color;
node->right = old->right;
node->left = old->left;
if (old->parent) {
if (old->parent->left == old)
old->parent->left = node;
else
old->parent->right = node;
}
else
root->rb_node = node;
old->left->parent = node;
if (old->right)
old->right->parent = node;
goto color;
}
/* only used for node is at most one degree node. */
parent = node->parent;
color = node->color;
if (child)
child->parent = parent;
if (parent) {
if (parent->left == node)
parent->left = child;
else
parent->right = child;
}
else
root->rb_node = child;
color:
if (color == RB_BLACK)
rb_delete_color(child, parent, root);
}
对于代码中的若干问题,以下作出说明(个人在上面也困惑良久)
问题1:如果删除结点为叶子结点,则进入rb_delete_color 后,child 为空,parent 的两个子结点均为空,如此判断方向是否会出错?事实上不会出错,因为红黑树的性质会保证。当删除结点为叶子结点时,只有当其为黑色时,才会进入函数rb_delete_color,由红黑树的定义,其parent 结点必定还有一个非空子结点,否则在删除前parent 结点就会违反性质5,即parent 结点的black hight 不一样了,所以这样判断方向不会有问题(在AVL树中就有问题了,所以传入一个方向的参数)
问题2:当parent 为空时,是否会出错?
parent 为空时,则表明删除结点的根结点,child 会成为新的根结点,所以在函数rb_delete_color 中while 判断node 是否为根结点时会直接退出,不会出错
问题3:rb_delete_color 函数中sibling 结点是否会无效?
由于删除了parent 某个子树的一个黑色结点,则其另一棵子树必定有黑色结点,否则就违反性质5了,所以sibling 结点一定存在