图——图的遍历——深度优先遍历DFS

    /*
    *Copyright (c) 2015 , 烟台大学计算机学院
    *All right resvered .
    *文件名称: 深度优先遍历DFS.cpp
    *作    者: 郑兆涵
    *图——图的遍历——深度优先遍历DFS
    */

问题：实现图遍历算法，输出深度优先遍历DFS

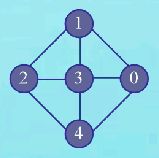
以此图为例：

编程代码：

//头文件：graph.h，包含定义图数据结构的代码、宏定义、要实现算法的函数的声明
#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED

#define MAXV 100                //最大顶点个数
#define INF 32767       //INF表示∞
typedef int InfoType;

//以下定义邻接矩阵类型
typedef struct
{
    int no;                     //顶点编号
    InfoType info;              //顶点其他信息，在此存放带权图权值
} VertexType;                   //顶点类型

typedef struct                  //图的定义
{
    int edges[MAXV][MAXV];      //邻接矩阵
    int n,e;                    //顶点数，弧数
    VertexType vexs[MAXV];      //存放顶点信息
} MGraph;                       //图的邻接矩阵类型

//以下定义邻接表类型
typedef struct ANode            //弧的结点结构类型
{
    int adjvex;                 //该弧的终点位置
    struct ANode *nextarc;      //指向下一条弧的指针
    InfoType info;              //该弧的相关信息,这里用于存放权值
} ArcNode;

typedef int Vertex;

typedef struct Vnode            //邻接表头结点的类型
{
    Vertex data;                //顶点信息
    int count;                  //存放顶点入度,只在拓扑排序中用
    ArcNode *firstarc;          //指向第一条弧
} VNode;

typedef VNode AdjList[MAXV];    //AdjList是邻接表类型

typedef struct
{
    AdjList adjlist;            //邻接表
    int n,e;                    //图中顶点数n和边数e
} ALGraph;                      //图的邻接表类型

//功能：由一个反映图中顶点邻接关系的二维数组，构造出用邻接矩阵存储的图
//参数：Arr - 数组名，由于形式参数为二维数组时必须给出每行的元素个数，在此将参数Arr声明为一维数组名（指向int的指针）
//      n - 矩阵的阶数
//      g - 要构造出来的邻接矩阵数据结构
void ArrayToMat(int *Arr, int n, MGraph &g); //用普通数组构造图的邻接矩阵
void ArrayToList(int *Arr, int n, ALGraph *&); //用普通数组构造图的邻接表
void MatToList(MGraph g,ALGraph *&G);//将邻接矩阵g转换成邻接表G
void ListToMat(ALGraph *G,MGraph &g);//将邻接表G转换成邻接矩阵g
void DispMat(MGraph g);//输出邻接矩阵g
void DispAdj(ALGraph *G);//输出邻接表G

#endif // GRAPH_H_INCLUDED



//源文件：graph.cpp，包含实现各种算法的函数的定义
#include <stdio.h>
#include <malloc.h>
#include "graph.h"

//功能：由一个反映图中顶点邻接关系的二维数组，构造出用邻接矩阵存储的图
//参数：Arr - 数组名，由于形式参数为二维数组时必须给出每行的元素个数，在此将参数Arr声明为一维数组名（指向int的指针）
//      n - 矩阵的阶数
//      g - 要构造出来的邻接矩阵数据结构
void ArrayToMat(int *Arr, int n, MGraph &g)
{
    int i,j,count=0;  //count用于统计边数，即矩阵中非0元素个数
    g.n=n;
    for (i=0; i<g.n; i++)
        for (j=0; j<g.n; j++)
        {
            g.edges[i][j]=Arr[i*n+j]; //将Arr看作n×n的二维数组，Arr[i*n+j]即是Arr[i][j]，计算存储位置的功夫在此应用
            if(g.edges[i][j]!=0)
                count++;
        }
    g.e=count;
}

void ArrayToList(int *Arr, int n, ALGraph *&G)
{
    int i,j,count=0;  //count用于统计边数，即矩阵中非0元素个数
    ArcNode *p;
    G=(ALGraph *)malloc(sizeof(ALGraph));
    G->n=n;
    for (i=0; i<n; i++)                 //给邻接表中所有头节点的指针域置初值
        G->adjlist[i].firstarc=NULL;
    for (i=0; i<n; i++)                 //检查邻接矩阵中每个元素
        for (j=n-1; j>=0; j--)
            if (Arr[i*n+j]!=0)      //存在一条边，将Arr看作n×n的二维数组，Arr[i*n+j]即是Arr[i][j]
            {
                p=(ArcNode *)malloc(sizeof(ArcNode));   //创建一个节点*p
                p->adjvex=j;
                p->info=Arr[i*n+j];
                p->nextarc=G->adjlist[i].firstarc;      //采用头插法插入*p
                G->adjlist[i].firstarc=p;
            }

    G->e=count;
}

void MatToList(MGraph g, ALGraph *&G)
//将邻接矩阵g转换成邻接表G
{
    int i,j;
    ArcNode *p;
    G=(ALGraph *)malloc(sizeof(ALGraph));
    for (i=0; i<g.n; i++)                   //给邻接表中所有头节点的指针域置初值
        G->adjlist[i].firstarc=NULL;
    for (i=0; i<g.n; i++)                   //检查邻接矩阵中每个元素
        for (j=g.n-1; j>=0; j--)
            if (g.edges[i][j]!=0)       //存在一条边
            {
                p=(ArcNode *)malloc(sizeof(ArcNode));   //创建一个节点*p
                p->adjvex=j;
                p->info=g.edges[i][j];
                p->nextarc=G->adjlist[i].firstarc;      //采用头插法插入*p
                G->adjlist[i].firstarc=p;
            }
    G->n=g.n;
    G->e=g.e;
}

void ListToMat(ALGraph *G,MGraph &g)
//将邻接表G转换成邻接矩阵g
{
    int i,j;
    ArcNode *p;
    g.n=G->n;   //根据一楼同学“举报”改的。g.n未赋值，下面的初始化不起作用
    g.e=G->e;
    for (i=0; i<g.n; i++)   //先初始化邻接矩阵
        for (j=0; j<g.n; j++)
            g.edges[i][j]=0;
    for (i=0; i<G->n; i++)  //根据邻接表，为邻接矩阵赋值
    {
        p=G->adjlist[i].firstarc;
        while (p!=NULL)
        {
            g.edges[i][p->adjvex]=p->info;
            p=p->nextarc;
        }
    }
}

void DispMat(MGraph g)
//输出邻接矩阵g
{
    int i,j;
    for (i=0; i<g.n; i++)
    {
        for (j=0; j<g.n; j++)
            if (g.edges[i][j]==INF)
                printf("%3s","∞");
            else
                printf("%3d",g.edges[i][j]);
        printf("\n");
    }
}

void DispAdj(ALGraph *G)
//输出邻接表G
{
    int i;
    ArcNode *p;
    for (i=0; i<G->n; i++)
    {
        p=G->adjlist[i].firstarc;
        printf("%3d: ",i);
        while (p!=NULL)
        {
            printf("-->%d/%d ",p->adjvex,p->info);
            p=p->nextarc;
        }
        printf("\n");
    }
}



//编写main函数，进行相关测试
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
int visited[MAXV];
void DFS(ALGraph *G, int v)
{
    ArcNode *p;
    int w;
    visited[v]=1;
    printf("%d ", v);
    p=G->adjlist[v].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            DFS(G,w);
        p=p->nextarc;
    }
}

int main()
{
    int i;
    ALGraph *G;
    int A[5][5]=
    {
        {0,1,0,1,0},
        {1,0,1,0,0},
        {0,1,0,1,1},
        {1,0,1,0,1},
        {0,0,1,1,0}
    };
    ArrayToList(A[0], 5, G);

    for(i=0; i<MAXV; i++) visited[i]=0;
    printf(" 由2开始深度遍历:");
    DFS(G, 2);
    printf("\n");

    for(i=0; i<MAXV; i++) visited[i]=0;
    printf(" 由0开始深度遍历:");
    DFS(G, 0);
    printf("\n");
    return 0;
}

输出结果：

学习心得：
对于深度优先遍历DFS首先是清楚DFS的算法过程：（由a→z）
（1）首先访问初始顶点a
（2）选择与顶点a相邻且没被访问过的顶点b为下一个顶点，再从b出发进行深度优先遍历搜索。
（3）直到图中与当前顶点a邻接的所有顶点被访问过为止。

例如：（此时可以有多种遍历顺序）

① 0 → 1 → 2 → 3 → 4
对于此遍历顺序，首先访问初始顶点0，再访问0的邻接顶点也就是下一个顶点1，此时与1相接的还可以再访问2，再由2访问3，最后3访问4.
② 0 → 3 → 2 → 1 → 4
而对于此遍历顺序，首先访问初始顶点0，再访问0下一个顶点3，与3相邻的，可以再访问2，再由2访问1，此时发现，与1相邻的所有其他的顶点都被访问过了，那此时，就应该回退到顶点1之前的那个顶点，选择另外一条路继续访问，也就是再由2访问4，而这之间的过程也牵扯到递归的返回问题。

DFS算法实现:
int visited[MAXV];//算法执行前全置0
void DFS(ALGraph *G, int v)
{
    ArcNode *p;
    int w;
    visited[v]=1;
    printf("%d ", v);
    p=G->adjlist[v].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            DFS(G,w);
        p=p->nextarc;
    }
}  

        首先需要定义一个全局变量visited[MAXV]这样一个全置为0的数组,而所定义的visited数组正是为了对下面DFS进行实现时运用的递归里面的值(包括返回)进行存储,这样在递归的不同层次上可以进行共享数据.
        在算法开始调用之后,会定义一个图G,指向当前的存储结构,还需要确定一个起始点,也就是int v.
        这里假设我们的起始点是0,则开始访问起始点0的时候,会将DFS(G,0),也就是将G访问0,然后将visited[v]=0;因此我们访问开始的节点也就是0了.
        接下来需要在0这个节点的邻接点中取寻找未被访问的节点,接下来直接通过firstarc,直接找到下一个节点1即可,接下来将p=G->adjust[v].firstarc ,也就是将p的值复制为0的下一个节点1,再将p赋值为p的nextarc,这样p就可以把0之后的每一个邻接点都访问到.
        接下来对while(p!=NULL)进行操作,将w赋值为p->nextarc,也就是将w赋值为p的下一个节点,也就是0的下一个邻接点1,然后判断visited[w]是否等于0,也就是visited[1]是否等于0,我们不难发现,visited[1]==0,
接下来就要去运用递归去调用函数DFS(G,1),此时形式参数v的值为取代为1.
        接下来就可以继续进行DFS深度遍历的实现了,接下来再进行visited[v]赋值为1,再接下来执行p=G->adjlist[v].firstarc时,我们会发现,p指向了1的下一个邻接点2,因为此时的visited[2]中的值还是0,所以我们需要再次调用DFS(G,w)也就是将w的值赋值为p的下一个节点,也就是1的下一个节点2,此时p指针指向2了.所以递归不会发生,直接p=p->nextarc,
则p会指向3,此时在发生调用DFS(G,3),再接下来是指向4,也是一样的道理.
        当我们访问完DFS(G,4)之后,节点4的邻接点还有2和3.它会继续按照步骤去判断2.3是否被访问过,当发现节点2.3都被访问过之后,4不再有未被访问的邻接点了.则DFS(G,4)结束,会通过递归的方式,返回DFS(G,3),由3再去判断其邻接点是否还有未被访问的,这样依次判断,最终将会放回
DFS(G,0).则递归结束,而整个的DFS深度遍历函数实现.

        
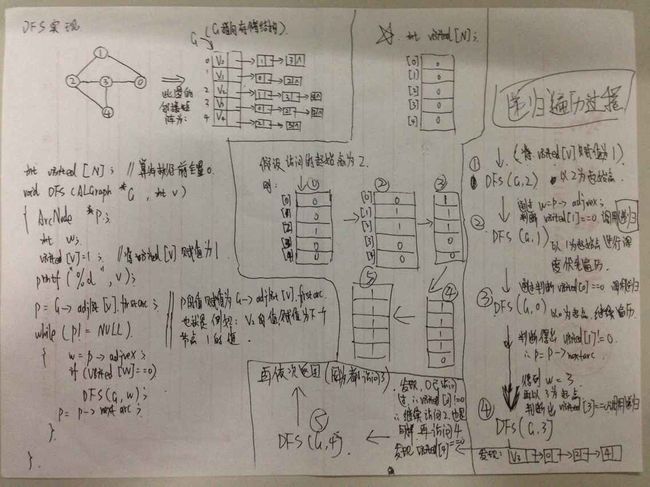
        下面是手写递归过程：