hdu-1053-Entropy && poj-1521-Entropy (哈夫曼编码)
Description
An entropy encoder is a data encoding method that achieves lossless data compression by encoding a message with “wasted” or “extra” information removed. In other words, entropy encoding removes information that was not necessary in the first place to accurately encode the message. A high degree of entropy implies a message with a great deal of wasted information; english text encoded in ASCII is an example of a message type that has very high entropy. Already compressed messages, such as JPEG graphics or ZIP archives, have very little entropy and do not benefit from further attempts at entropy encoding.
English text encoded in ASCII has a high degree of entropy because all characters are encoded using the same number of bits, eight. It is a known fact that the letters E, L, N, R, S and T occur at a considerably higher frequency than do most other letters in english text. If a way could be found to encode just these letters with four bits, then the new encoding would be smaller, would contain all the original information, and would have less entropy. ASCII uses a fixed number of bits for a reason, however: it’s easy, since one is always dealing with a fixed number of bits to represent each possible glyph or character. How would an encoding scheme that used four bits for the above letters be able to distinguish between the four-bit codes and eight-bit codes? This seemingly difficult problem is solved using what is known as a “prefix-free variable-length” encoding.
In such an encoding, any number of bits can be used to represent any glyph, and glyphs not present in the message are simply not encoded. However, in order to be able to recover the information, no bit pattern that encodes a glyph is allowed to be the prefix of any other encoding bit pattern. This allows the encoded bitstream to be read bit by bit, and whenever a set of bits is encountered that represents a glyph, that glyph can be decoded. If the prefix-free constraint was not enforced, then such a decoding would be impossible.
Consider the text “AAAAABCD”. Using ASCII, encoding this would require 64 bits. If, instead, we encode “A” with the bit pattern “00”, “B” with “01”, “C” with “10”, and “D” with “11” then we can encode this text in only 16 bits; the resulting bit pattern would be “0000000000011011”. This is still a fixed-length encoding, however; we’re using two bits per glyph instead of eight. Since the glyph “A” occurs with greater frequency, could we do better by encoding it with fewer bits? In fact we can, but in order to maintain a prefix-free encoding, some of the other bit patterns will become longer than two bits. An optimal encoding is to encode “A” with “0”, “B” with “10”, “C” with “110”, and “D” with “111”. (This is clearly not the only optimal encoding, as it is obvious that the encodings for B, C and D could be interchanged freely for any given encoding without increasing the size of the final encoded message.) Using this encoding, the message encodes in only 13 bits to “0000010110111”, a compression ratio of 4.9 to 1 (that is, each bit in the final encoded message represents as much information as did 4.9 bits in the original encoding). Read through this bit pattern from left to right and you’ll see that the prefix-free encoding makes it simple to decode this into the original text even though the codes have varying bit lengths.
As a second example, consider the text “THE CAT IN THE HAT”. In this text, the letter “T” and the space character both occur with the highest frequency, so they will clearly have the shortest encoding bit patterns in an optimal encoding. The letters “C”, “I’ and “N” only occur once, however, so they will have the longest codes.
There are many possible sets of prefix-free variable-length bit patterns that would yield the optimal encoding, that is, that would allow the text to be encoded in the fewest number of bits. One such optimal encoding is to encode spaces with “00”, “A” with “100”, “C” with “1110”, “E” with “1111”, “H” with “110”, “I” with “1010”, “N” with “1011” and “T” with “01”. The optimal encoding therefore requires only 51 bits compared to the 144 that would be necessary to encode the message with 8-bit ASCII encoding, a compression ratio of 2.8 to 1.
Input
The input file will contain a list of text strings, one per line. The text strings will consist only of uppercase alphanumeric characters and underscores (which are used in place of spaces). The end of the input will be signalled by a line containing only the word “END” as the text string. This line should not be processed.
Output
For each text string in the input, output the length in bits of the 8-bit ASCII encoding, the length in bits of an optimal prefix-free variable-length encoding, and the compression ratio accurate to one decimal point.
Sample Input
AAAAABCD
THE_CAT_IN_THE_HAT
END
Sample Output
64 13 4.9
144 51 2.8
题意:给一个有大写字母和下划线组成的字符串,输出用ascii编码是使用的字节数 和 用哈夫曼编码所使用的字节数 和 他们的比值
思路:ascii编码使用的字节数就是字符个数乘8,关键是哈夫曼编码。
什么是哈夫曼编码?
首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树,使用的是贪心思想。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+…+Wn*Ln),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。可以证明哈夫曼树的WPL是最小的。
哈夫曼编码步骤:
一、对给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,…,Ti,…,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算 法,一般还要求以Ti的权值Wi的升序排列。)
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
这样就构造成了一颗哈夫曼树
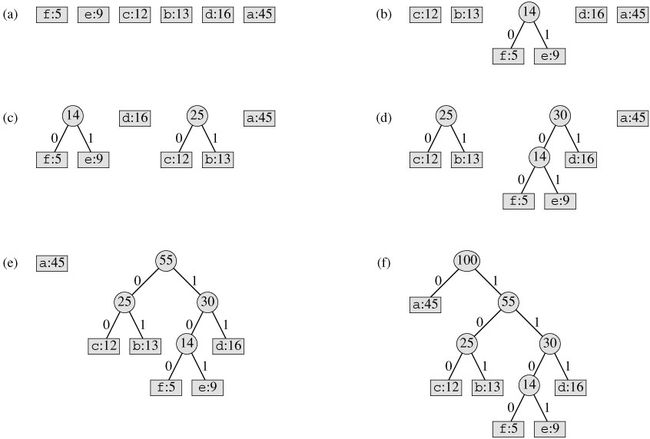
下图是百度上找的图片,画出了建立一颗哈夫曼树的过程。
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <queue>
#include <algorithm>
#define N 30
using namespace std;
struct node
{
int left, right, father, num, index, len;
char c;
friend bool operator < (node a, node b)
{
return a.num > b.num;
}
}ch[N<<1];
string str;
priority_queue<node> q;
int l;
int count ()
{
int i, num[30], ret = 0;
memset(num, 0, sizeof(num));
for (i = 0; i < l; i++)
{
if (str[i] == '_')
num[26]++;
else
num[str[i]-'A']++;
}
while(!q.empty()) q.pop();
for (i = 0; i < 27; i++)
{
if (num[i])
{
ch[ret].num = num[i];
ch[ret].index = ret;
ch[ret].c = i+'A';
q.push(ch[ret++]);
}
}
return ret;
}
int ecode(int n)
{
int t, i;
node t1, t2;
for (i = n; i < 2*n-1; i++)
{
t1 = q.top();
q.pop();
t2 = q.top();
q.pop();
ch[i].left = t1.index;
ch[i].right = t2.index;
ch[i].index = i;
ch[i].num = ch[t1.index].num+ch[t2.index].num;
ch[t1.index].father = i;
ch[t2.index].father = i;
q.push(ch[i]);
}
int ans = 0;
for (i = 0; i < n; i++)
{
ch[i].len = 0;
t = i;
while(ch[t].father)
{
ch[i].len++;
t = ch[t].father;
}
ans += ch[i].num*ch[i].len;
}
return ans;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
int ans1, ans2, ret;
while(1)
{
memset(ch, 0, sizeof(ch));
cin >> str;
if (str == "END") break;
l = str.size();
ans1 = l*8;
ret = count();
if (ret == 1) ans2 = l;
else ans2 = ecode(ret);
cout.setf(ios::fixed);
cout << ans1 << ' ' << ans2 << ' ' << setprecision(1) << 1.0*ans1/ans2 << endl;
}
return 0;
}