HDU-4587 TWO NODES (割点[Tarjan])
TWO NODES
http://acm.hdu.edu.cn/showproblem.php?pid=4587
Time Limit: 24000/12000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Problem Description
Suppose that G is an undirected graph, and the value of
stab is defined as follows:
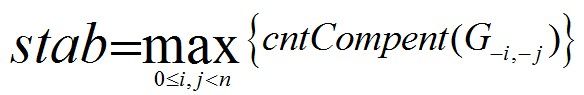
Among the expression,G -i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.
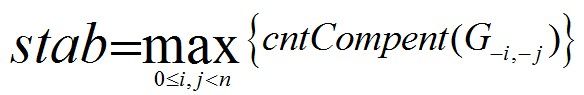
Among the expression,G -i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.
Input
The input will contain the description of several graphs. For each graph, the description consist of an integer N for the number of nodes, an integer M for the number of edges, and M pairs of integers for edges (3<=N,M<=5000).
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.
Output
For each graph in the input, you should output the value of
stab.
Sample Input
4 5 0 1 1 2 2 3 3 0 0 2
Sample Output
2
题目大意:给定一个无向图,求删除两点后,图的连通分量数的最大值?
昨天做时,还没学Tarjan,只会枚举后各种“贪心”求解,经过今天那么多铺垫后,发现这也是到比较简单的题,枚举第一个删除的点,然后就转化为——求删除其他一点后,图的连通分量数的最大值 了
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int MAXN=5005;
int n,m,num,ans,cnt,del;
int low[MAXN],dfn[MAXN],blocks[MAXN];//biocks[i]表示删掉i点后,能形成的连通块数
vector<int> g[MAXN];
void Tarjan(int u,int p) {
dfn[u]=low[u]=++num;
int v;
for(int i=0;i<g[u].size();++i) {
v=g[u][i];
if(v!=del&&v!=p) {
if(dfn[v]==0) {
Tarjan(v,u);
low[u]=min(low[u],low[v]);
if(dfn[u]<=low[v])//删去点u后的连通分量数+1
++blocks[u];
}
else if(dfn[v]<low[u])
low[u]=dfn[v];
}
}
}
int main() {
int s,e;
while(scanf("%d%d",&n,&m)==2) {
for(int i=0;i<n;++i)
g[i].clear();
while(m-->0) {
scanf("%d%d",&s,&e);
g[s].push_back(e);
g[e].push_back(s);
}
ans=0;
for(int k=0;k<n;++k) {
del=k;//表示将k点删除
num=cnt=0;
for(int i=0;i<n;++i) {
dfn[i]=0;
blocks[i]=1;//默认删除点i后,其父亲节点存在一个连通分量
}
dfn[del]=0x3f3f3f3f;
for(int i=0;i<n;++i) {
if(dfn[i]==0) {
++cnt;//cnt表示连通分量数
blocks[i]=0;//根结点无父亲结点,即其无父亲结点的连通分量
Tarjan(i,-1);
}
}
for(int i=0;i<n;++i)
if(i!=del)
ans=max(ans,cnt-1+blocks[i]);//cnt-1表示除去i所在的连通分量后的连通分量数;blocks[i]表示i所在连通分量在删除i点后的连通分量数
}
printf("%d\n",ans);
}
return 0;
}