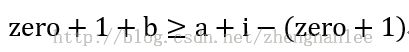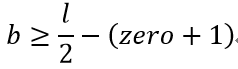[NOIP 2014复习]第七章：数学

1、递推

2、组合数学

1、POJ 3252 Round Numbers

http://poj.org/problem?id=3252

题目大意：给出a,b，求区间[a,b]中数字转换为二进制后，0比1个数多的数字(Round Number)个数

首先打表求出所需的组合数C(i,j)，题目可转换为求区间[0,x)中的Round Number个数，分两类讨论：

1、转二进制后长度比x小的Round Number个数，令x的二进制长度为l，易证其为C[i][i/2+1]+C[i][i/2+2]+....+C[i][i],i∈[1,l)

2、转二进制后长度和x一样的Round Number个数，先来看一看这个二进制的x：

如果第四位绿色的1改成0，那么它后面无论是0是1，改后的数一定比原来的小，但是不能乱改，改后的数字一定要保证0比1个数多，可以设x的绿色数字之前的0的个数为zero,

i是从后往前数绿色1的位置，a为上图中空格里1的个数，b为空格里0的个数

有如下等式：

有如下不等式：

解得：

则Round Number个数为C[i-1][j],j

 

#include<iostream>

using namespace std;

int c[33][33] = { 0 };
int bin[35];  //十进制n的二进制数

void combinations()
{
	for (int i = 0; i <= 32; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			if (!j || i == j)
			{
				c[i][j] = 1;
			}
			else
			{
				c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
			}
		}
	}
	return;
}

void dec_to_bin(int n)
{
	bin[0] = 0;
	while (n)
	{
		bin[++bin[0]] = n % 2;
		n /= 2;
	}
	return;
}

int round(int n)
{
	int i, j;
	int sum = 0;
	dec_to_bin(n);

	/*计算长度小于bin[0]的所有二进制数中RN的个数*/

	for (i = 1; i < bin[0] - 1; i++)
	{
		for (j = i / 2 + 1; j <= i; j++)
		{
			sum += c[i][j];
		}
	}
			
	/*计算长度等于bin[0]的所有二进制数中RN的个数*/

	int zero = 0;  //从高位向低位搜索过程中出现0的位的个数
	for (i = bin[0] - 1; i >= 1; i--)
	{
		if (bin[i])
		{
			for (j = (bin[0] + 1) / 2 - (zero + 1); j <= i - 1; j++)
			{
				sum += c[i - 1][j];
			}
		}
		else zero++;
	}
	return sum;
}

int main()
{
	combinations();
	int a, b;
	while (cin >> a >> b)
	{
		cout << round(b + 1) - round(a) << endl;
	}
}

 

 

3、群论

4、数论

1、POJ 2142 The Balance

http://poj.org/problem?id=2142

题目大意：求ax+by=n的最小正整数解

思路：可以将上式转化为a(x/n)+b(y/n)=1，很明显就可以用扩展欧几里得来做了，由于x/n和y/n中必然有一个是小于零的，所以要将其中小于零的那个转化为最小正整数解（要么以x为主变x,要么以y为主变y），取x+y的值小的那个转化方案

/*
    题目大意：求ax+by=n的x和y的最小正整数解
    转化为求a(x/n)+b(y/n)=1的解
*/
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>

using namespace std;

int gcd(int a,int b)
{
    if(b==0) return a;
    return gcd(b,a%b);
}

int extendGCD(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int gcdab=extendGCD(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return gcdab;
}

int main()
{
    int a,b,n;
    while(scanf("%d%d%d",&a,&b,&n)&&(a!=0||b!=0||n!=0))
    {
        int x,y;
        int gcdab=gcd(a,b); //先让a和b互质
        a/=gcdab;
        b/=gcdab;
        n/=gcdab;
        gcdab=extendGCD(a,b,x,y); //现在的x还是x/n，y还是y/n
        //方案1：以x为主，将x转化为最小正数，y跟着变
        int newx=((x*n)%b+b)%b; //x化为最小正数
        int newy=(n-a*newx)/b;
        if(newy<0) newy=-newy;
        //方案2：以y为主：将y转化为最小正数，x跟着变
        y=((y*n)%a+a)%a; //y化为最小正数
        x=(n-b*y)/a;
        if(x<0) x=-x;
        //现在从方案1、2中选一个x+y最小的方案
        if(x+y>newx+newy)
            x=newx,y=newy;
        printf("%d %d\n",x,y);
    }
    return 0;
}

5、博弈

6、线性代数

7、数学函数

8、抽屉原理、容斥原理

1、POJ 3370 Halloween Treats

http://poj.org/problem?id=3370

题目大意：给出数字c、n(c<=n)和n个数，要你找出其中的一些数，使得这些数之和mod c=0，答案不唯一

思路：

首先构造前缀和数组sum[],sum[i]=前i个数字之和，然后对每个sum[i]mod c

由于c<=n，所以此题可以分两种情况进行讨论：

1、c=n,则要么有i<j使得sum[i]=sum[j]，要么一定有一个sum[i]=0（证明略）

2、c<n，由抽屉原理易知，一定有i<j使得sum[i]=sum[j]

 

对于存在sum[i]=0的情况，答案即为[1,i],对于sum[i]=sum[j]的情况，sum[j]-sum[i]=0，答案为[i,j]

 

接下来构造剩余类抽屉remainder[],remainder[i]为最大的sum[x]=i的下标x，遍历sum数组，如果sum[i]归属的抽屉已经保存了一个元素的下标x，那么答案就是[x,i]，并且不需要继续遍历了，如果sum[i]=0，答案就是[1,i]，也不需要继续遍历

/*
    思路：鸽巢原理（抽屉原理）
    由于c<=邻居个数n，所以在这n个数中，一定有一个或两个数都能整除c,若有两个数能整除c，则这两个数中间所有数之和也能被c整除
*/
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>

#define MAXN 100010

using namespace std;

int sweet[MAXN]; //每个邻居的糖果个数
int sum[MAXN]; //sum[i]=前i项的和
int remainder[MAXN];

int main()
{
    int c,n;
    while(scanf("%d%d",&c,&n)&&n&&c)
    {
        int head=1,tail=1;
        memset(sweet,0,sizeof(sweet));
        memset(sum,0,sizeof(sweet));
        memset(remainder,0,sizeof(remainder));
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&sweet[i]);
            sum[i]=(sum[i-1]+sweet[i])%c; //求前i个数之和mod c
        }
        for(int i=1;i<=n;i++)
        {
            if(sum[i]==0) //找到了一个i使得前i个数之和mod c=0
            {
                tail=i;
                break;
            }
            if(remainder[sum[i]]>0)
            {
                head=remainder[sum[i]]+1;
                tail=i;
                break;
            }
            remainder[sum[i]]=i; //更新前i个数之和的余数对应的最大编号
        }
        for(int i=head;i<=tail;i++) printf("%d ",i);
        printf("\n");
    }
    return 0;
}