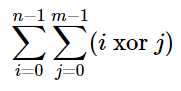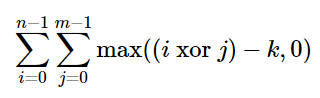bzoj4513【SDOI2016】储能表

4513: [Sdoi2016]储能表

Time Limit: 10 Sec   Memory Limit: 128 MB
Submit: 340   Solved: 182
[ Submit][ Status][ Discuss]

Description

有一个 n 行 m 列的表格，行从 0 到 n−1 编号，列从 0 到 m−1 编号。每个格子都储存着能量。最初，第 i 行第 j 列的格子储存着 (i xor j) 点能量。所以，整个表格储存的总能量是，

随着时间的推移，格子中的能量会渐渐减少。一个时间单位，每个格子中的能量都会减少 1。显然，一个格子的能量减少到 0 之后就不会再减少了。

也就是说，k 个时间单位后，整个表格储存的总能量是，

给出一个表格，求 k 个时间单位后它储存的总能量。

由于总能量可能较大，输出时对 p 取模。

Input

第一行一个整数 T，表示数据组数。接下来 T 行，每行四个整数 n、m、k、p。

Output

 共 T 行，每行一个数，表示总能量对 p 取模后的结果

Sample Input

3
2 2 0 100
3 3 0 100
3 3 1 100

Sample Output

2
12
6

HINT

 T=5000，n≤10^18，m≤10^18，k≤10^18，p≤10^9

Source

鸣谢Menci上传

灰常麻烦的数位DP(二进制数位)

f[i][1/0][1/0][1/0]表示DP到第i位，等于/小于n，等于/小于n，等于/大于k的数对的个数。

g[i][1/0][1/0][1/0]表示DP到第i位，等于/小于n，等于/小于n，等于/大于k的数对异或值的和。

然后从高位到低位DP转移。

为什么要从高到低呢？因为只有这样才可以限制是否达到上界或下界。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
using namespace std;
ll t,n,m,k,p,ans,f[100][2][2][2],g[100][2][2][2],bin[100];
inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int main()
{
	t=read();
	while (t--)
	{
		n=read()-1;m=read()-1;k=read();p=read();
		bin[0]=1;F(i,1,60) bin[i]=bin[i-1]*2%p;
		ans=0;
		memset(f,0,sizeof(f));memset(g,0,sizeof(g));
		f[0][1][1][1]=1;
		F(i,0,60) F(a,0,1) F(b,0,1) F(c,0,1) if (f[i][a][b][c])
		{
			ll tn=n&(1ll<<(60-i))?1:0,tm=m&(1ll<<(60-i))?1:0,tk=k&(1ll<<(60-i))?1:0;
			F(x,0,1) if (!a||x<=tn) F(y,0,1) if (!b||y<=tm)
			{
				int z=x^y;
				if (c&&z<tk) continue;
				int ta=(a&&x==tn)?1:0,tb=(b&&y==tm)?1:0,tc=(c&&z==tk)?1:0;
				(f[i+1][ta][tb][tc]+=f[i][a][b][c])%=p;
				(g[i+1][ta][tb][tc]+=g[i][a][b][c])%=p;
				if (z) (g[i+1][ta][tb][tc]+=bin[60-i]*f[i][a][b][c]%p)%=p;
			}
		}
		F(a,0,1) F(b,0,1) F(c,0,1) ans=((ans+g[61][a][b][c]-k%p*f[61][a][b][c]%p)%p+p)%p;
		printf("%lld\n",ans);
	}
	return 0;
}