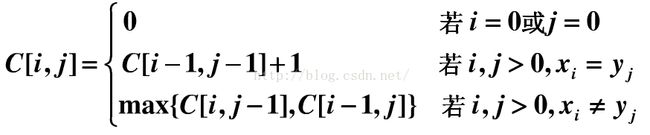最长公共子序列问题 (LCS)
最长公共子序列问题 :
1>给两个子序列A和B,求长度最大的公共子序列。例如1,5,2,6,8,7和2,3,5,6,9,8,4的最长公共子序列为5,6,8(另一个解是2,6,8)。
2>我们称序列Z = < z1, z2, ..., zk >是序列X = < x1, x2, ..., xm >的子序列当且仅当存在严格上升的序列< i1, i2, ..., ik >,使得对j = 1, 2, ... ,k, 有xij = zj。比如Z = < a, b, f, c > 是X = < a, b, c, f, b, c >的子序列。
现在给出两个序列X和Y,你的任务是找到X和Y的最大公共子序列,也就是说要找到一个最长的序列Z,使得Z既是X的子序列也是Y的子序列。
举个例子:cnblogs这个字符串中子序列有多少个呢?很显然有27个,比如其中的cb,cgs等等都是其子序列,我们可以看出
子序列不见得一定是连续的,连续的那是子串。
我想大家已经了解了子序列的概念,那现在可以延伸到两个字符串了,那么大家能够看出:cnblogs和belong的公共子序列吗?
在你找出的公共子序列中,你能找出最长的公共子序列吗?
从图中我们看到了最长公共子序列为blog,仔细想想我们可以发现其实最长公共子序列的个数不是唯一的,可能会有两个以上,
但是长度一定是唯一的,比如这里的最长公共子序列的长度为4。
思路如下面的图:
方案:既然是经典的题目肯定是有优化空间的,并且解题方式是有固定流程的,这里我们采用的是矩阵实现,也就是二维数组。
第一步:先计算最长公共子序列的长度。
第二步:根据长度,然后通过回溯求出最长公共子序列。
现有两个序列X={x1,x2,x3,...xi},Y={y1,y2,y3,....,yi},
设一个C[i,j]: 保存Xi与Yj的LCS的长度。
动态规划的一个重要性质特点就是解决“子问题重叠”的场景,可以有效的避免重复计算,根据上面的
公式其实可以发现C[i,j]一直保存着当前(Xi,Yi)的最大子序列长度。
如下代码:
#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int smax(int x,int y){
return x >=y ? x : y;
}
int maxstr[10000][10000];
char str1[1000],str2[1000];
int main(){
int len1,len2;
while(scanf("%s%s",&str1, &str2)!=EOF){
len1=strlen(str1);
len2=strlen(str2);
for(int i=0; i<=len1; ++i){
maxstr[i][0]=0;//初始化边界,过滤掉0的情况
}
for(int i=0; i<=len2; ++i){
maxstr[0][i]=0;
}
//填充矩阵
for(int i=1; i<=len1; ++i){
for(int j=1; j<=len2; ++j){
if(str1[i-1]==str2[j-1])//相等的情况
maxstr[i][j]=maxstr[i-1][j-1]+1;
else if(maxstr[i-1][j] >= maxstr[i][j-1]){//比较“左边”和“上边“,根据其max来填充
maxstr[i][j]=maxstr[i-1][j];
}else{
maxstr[i][j]=maxstr[i][j-1];
}
}
}
printf("%d\n",maxstr[len1][len2]);
}
return 0;
}
参考博客:http://www.cnblogs.com/huangxincheng/archive/2012/11/11/2764625.html
参考博客:http://blog.csdn.net/chenwenshi/article/details/6027884