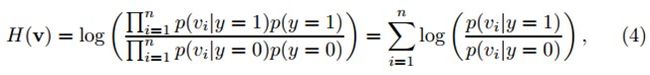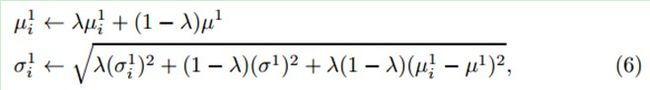机器学习算法学习与总结——朴素贝叶斯分类器
机器学习算法学习与总结——朴素贝叶斯分类器
朴素贝叶斯算法是目前非常流行的机器学习分类算法，在垃圾邮件过滤、文本分类，手写数字识别等领域。朴素贝叶斯算法的算法思想是：对于给定的输入样本，在已知先验概率，和样本类别的概率分布模型（已知属于某一类别的前提下样本发生的条件概率分布）的前提下，通过贝叶斯公式求得样本类别的后验概率，将后验概率最大的样本所属的类作为分类器的输出。
从上述算法思想可以看出，模型优点是：1.算法数学模型稳定，分类效果较好。2。训练参数少，模型学习简单。模型的缺点：1，贝叶斯分类器算法要求样本之间相互独立，对于样本之间关联性比较强的样本分类效果比较差。2.因为需要事先知道样本的先验概率。3 需要利用大量样本技术样本类别的概率分布，因此少量样本分类效果差。
朴素贝叶斯分类器的算法原理和数学基础：
贝叶斯定理和贝叶斯公式：
条件概率——在事件B发生的条件下，事件A发生的概率 P（A|B）=P（AB）/P(B)
乘法定理——P（AB）= P（A|B）P(B)
全概率公式——P(A) = P(A|B1)*P(B1) + P(A|B2)*P(B2)+…+P(A|Bn)*P(Bn)
贝叶斯定理——在已知事件A的先验概率和在事件B发生的条件下，事件A发生的条件概率P（A|B）的情况下，A的后验概率P（B|A）= P（A|B）P（B）/P(A)
贝叶斯公式——根据贝叶斯定理和全概率公式得到：
（1）
朴素贝叶斯分类的正式定义如下：
1、设
为一个待分类项，而每个a为x的一个特征属性。
2、有类别集合
。
3、计算
。
4、如果
，则
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：
1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即
。
3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：
(2)
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：
(3)
后验概率最大化的含义：朴素贝叶斯算法将实例分到后验概率最大的类中，这等价于期望风险最小化也就是损失函数的值最小。这样以一来，我们可以根据期望风险最小化准则就得到了后验概率最大化准则。
朴素贝叶斯算法应用实例一：压缩感知目标跟踪中的分类器
对每个样本z（m维向量），它的低维表示是v（n维向量，n远小于m）。假定v中的各元素是独立分布的。可以通过朴素贝叶斯分类器来建模。在y=0表示负样本，y=1表示正样本由上述公式3可得：
其中，y∊{0,1}代表样本标签，y=0表示负样本，y=1表示正样本，假设两个类的先验概率相等。p(y=1)=p(y=0)=0.5。Diaconis和Freedman证明了高维随机向量的随机投影几乎都是高斯分布的。因此，我们假定在分类器H(v)中的条件概率p(vi|y=1)和p(vi|y=0)也属于高斯分布，并且可以用四个参数来描述：
（5）
上式中的四个参数会进行增量更新：
式中，学习因子λ>0，
上式可以由最大化似然估计得到。
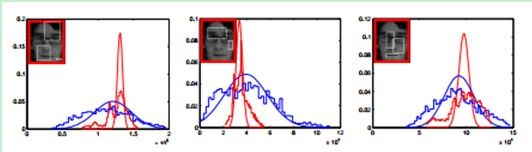
图中显示了从某帧中的正样本和负样本提取出的三个不同特征（低维空间下）的概率分布。红色和蓝色阶梯线分别代表正样本和负样本的直方图。而红色和蓝色的曲线表示通过我们的增量更新模型得到的相应的分布估计。图说明了在投影空间，通过上式描述的在线更新的高斯分布模型是特征的一个良好估计。我们通过最大似然估计更新条件概率分布中参数的值，竟而更新朴素贝叶斯分类器。与此同时将H(v)最大的位置作为目标的位置。
相关实现代码：
// Update the mean and variance of the gaussian classifier
//论文中是通过用高斯分布去描述样本的每一个harr特征的概率分布的。高斯分布就可以通过期望和方差
//两个参数来表征。然后通过正负样本的每一个harr特征高斯概率分布的对数比值，来构建分类器决策
//该box属于目标还是背景。这里计算新采集到的正负样本的特征的期望和标准差，并用其来更新分类器
void CompressiveTracker::classifierUpdate(Mat& _sampleFeatureValue, vector<float>& _mu, vector<float>& _sigma, float _learnRate)
{
Scalar muTemp;
Scalar sigmaTemp;
for (int i=0; i<featureNum; i++)
{
//计算所有正样本或者负样本的某个harr特征的期望和标准差
meanStdDev(_sampleFeatureValue.row(i), muTemp, sigmaTemp);
//这个模型参数更新的公式见论文的公式6
_sigma[i] = (float)sqrt( _learnRate*_sigma[i]*_sigma[i]+ (1.0f-_learnRate)*sigmaTemp.val[0]*sigmaTemp.val[0]
+ _learnRate*(1.0f-_learnRate)*(_mu[i]-muTemp.val[0])*(_mu[i]-muTemp.val[0]));// equation 6 in paper
_mu[i] = _mu[i]*_learnRate + (1.0f-_learnRate)*muTemp.val[0];// equation 6 in paper
}
}
// Compute the ratio classifier
void CompressiveTracker::radioClassifier(vector<float>& _muPos, vector<float>& _sigmaPos, vector<float>& _muNeg, vector<float>& _sigmaNeg, Mat& _sampleFeatureValue, float& _radioMax, int& _radioMaxIndex)
{
float sumRadio;
//FLT_MAX是最大的浮点数的宏定义，那么-FLT_MAX就是最小的浮点数了
//这个是拿来存放 那么多box中最大的分类分数的
_radioMax = -FLT_MAX;
//这个是对应于上面那个，是存放分类分数最大的那个box的
_radioMaxIndex = 0;
float pPos;
float pNeg;
int sampleBoxNum = _sampleFeatureValue.cols;
for (int j=0; j<sampleBoxNum; j++) //每帧采样得到的需要检测的box
{
sumRadio = 0.0f;
for (int i=0; i<featureNum; i++) //每个box的需要匹配的特征数
{
//计算每个特征的概率，特征分布近似于高斯分布，故将描述该特征的均值和标准差代入高斯模型就可以
//得到，分别在正样本和负样本的基础上，出现该特征的概率是多少。如果正样本时候的概率大，那么
//我们就说，这个特征对应的样本是正样本。数学上比较大小，就是减法或者除法了，这里是取对数比值
pPos = exp( (_sampleFeatureValue.at<float>(i,j)-_muPos[i])*(_sampleFeatureValue.at<float>(i,j)- _muPos[i]) / -(2.0f*_sigmaPos[i]*_sigmaPos[i]+1e-30) ) / (_sigmaPos[i]+1e-30);
pNeg = exp( (_sampleFeatureValue.at<float>(i,j)-_muNeg[i])*(_sampleFeatureValue.at<float> (i,j)-_muNeg[i]) / -(2.0f*_sigmaNeg[i]*_sigmaNeg[i]+1e-30) ) / (_sigmaNeg[i]+1e-30);
//paper的方程4：计算分类结果，得到一个分数，这个分数是由一个样本或者box的50个特征（弱分类）
//进入分类器分类得到的结果总和（强分类？）。表征的是目前这个box的特征属于正样本（目标）的
//可能性大小。哪个分数最大，自然我就认为你是目标了。（当然，在具体应用中需要加一些策略去
//改善误跟踪的情况。例如如果最高的分数都达不到一个阈值，那就不存在目标等）
sumRadio += log(pPos+1e-30) - log(pNeg+1e-30);// equation 4
}
if (_radioMax < sumRadio) //拿到最大的分数和相应的box索引
{
_radioMax = sumRadio;
_radioMaxIndex = j;
}
}
}
朴素贝叶斯算法应用实例二——文本分类算法：
http://blog.csdn.net/lavorange/article/details/17841383
参考文献：
http://blog.csdn.net/zouxy09/article/details/8210176
http://blog.csdn.net/lavorange/article/details/17841383
李航的《统计机器学习》