hdu 4858 项目管理(图的分治)

项目管理

Problem Description

我们建造了一个大项目！这个项目有n个节点，用很多边连接起来，并且这个项目是连通的！
两个节点间可能有多条边，不过一条边的两端必然是不同的节点。
每个节点都有一个能量值。

现在我们要编写一个项目管理软件，这个软件呢有两个操作：
1.给某个项目的能量值加上一个特定值。
2.询问跟一个项目相邻的项目的能量值之和。（如果有多条边就算多次，比如a和b有2条边，那么询问a的时候b的权值算2次）。

 

Input

第一行一个整数T(1 <= T <= 3),表示测试数据的个数。
然后对于每个测试数据，第一行有两个整数n(1 <= n <= 100000)和m(1 <= m <= n + 10)，分别表示点数和边数。

然后m行，每行两个数a和b，表示a和b之间有一条边。
然后一个整数Q。

然后Q行，每行第一个数cmd表示操作类型。如果cmd为0，那么接下来两个数u v表示给项目u的能量值加上v(0 <= v <= 100)。
如果cmd为1，那么接下来一个数u表示询问u相邻的项目的能量值之和。

所有点从1到n标号。

 

Output

对每个询问，输出一行表示答案。

 

Sample Input

   
   
   
   

    
    
    
    1
3 2
1 2
1 3
6
0 1 15
0 3 4
1 1
1 3
0 2 33
1 2
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    4
15
15
   
   
   
   

 

Author

CLJ

 

Source

BestCoder Round #1

 

共有m条边 设k=sqrt（m) 若一个点的度（即与之有边连接点的个数）小于k成为轻点，剩下的（大于等于k）称为重点

对点i来说degree[i]记录点的度

重点的个数 <=2*m/sqrt(m)=2*sqrt(m)

对于一个点i，A[i]记录这个点的值

对于重点i，sum[i]记录其答案，

对于轻点i，sum[i]无任何作用，轻点的答案通过对所有与轻点相连的点的值求和直接得到

题目可分为三个过程

1.构造图

        对点i来说

        如果i点是轻点，则记录所有与他相连的点到point[i]中

        如果i点是重点，则记录所有与他相连的重点到point[i]中

2.更新图

        对点i来说

        如果i点是轻点，则更新point[i]中所有重点，即为更新所有与之相连的重点的sum值

        如果i点是重点，则更新point[i]中所有点，也即为更新所有与之相连的重点的sum值

3.查询点

       对点i来说

       如果i点是轻点，则累加所有与之相连的点的值直接求出解

       如果i点是重点，则直接输出sum[i]，因为sum[i]的值已经更新过了（与重点相连的点有两种——轻点与重点，在2.更新图过程中都完成了更新）

稍微计算一下，就能发现此种方法在点多且密集的情况下，比基础方法快了很多

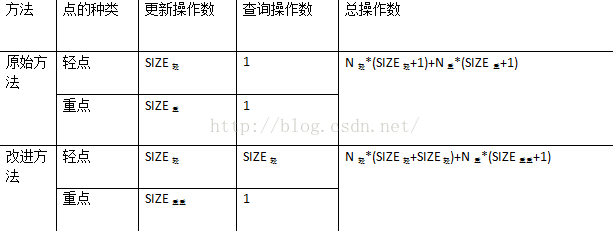
设轻点个数为N轻，重点个数为N重，轻点所相连点的个数为SIZE轻，重点所相连的个数为SIZE重，重点所相连的重点个数为SIZE重重（重点的个数 <=2*m/sqrt(m)=2*sqrt(m)=2*k=2*SIZE轻）

 

 忽略N轻与N重 

 

故比较SIZE重与SIZE轻+SIZE重重（SIZE重重<=2*k约等于2*SIZE轻）

              左式=m             右式=3*sqrt(m)

在点多且边密集的图中，显然改进方法的速度有了很大的提升

#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int MAX=100105;
struct node
{
    int u,v;
}edge[MAX];;
int k;
vector<int>point[MAX];
int A[MAX],sum[MAX],degree[MAX];
void update(int x,int d)
{
    int i;
    A[x]+=d;
    for(i=0;i<point[x].size();i++)
        if(degree[point[x][i]]>=k)
            sum[point[x][i]]+=d;
}
int query(int x)
{
    if(degree[x]<k)
    {
        int ans=0;
        for(int i=0;i<point[x].size();i++)
            ans+=A[point[x][i]];
        return ans;
    }
    else
        return sum[x];
}
int main()
{
    int T,n,m,i,u,v,Q,cmd,a,b;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        memset(A,0,sizeof(A));
        memset(degree,0,sizeof(degree));
        memset(sum,0,sizeof(sum));
        for(i=1;i<=n;i++)
            point[i].clear();
        for(i=1;i<=m;i++)
        {
            scanf("%d%d",&edge[i].u,&edge[i].v);
            degree[edge[i].u]++;
            degree[edge[i].v]++;
        }
        k=sqrt(m);
        for(i=1;i<=m;i++)
        {
            u=edge[i].u;
            v=edge[i].v;
            if(degree[u]<k)
                point[u].push_back(v);
            else if(degree[v]>=k)
                point[u].push_back(v);
            if(degree[v]<k)
                point[v].push_back(u);
            else if(degree[u]>=k)
                point[v].push_back(u);
        }
        scanf("%d",&Q);
        while(Q--)
        {
            scanf("%d",&cmd);
            if(cmd==0)
            {
                scanf("%d%d",&a,&b);
                update(a,b);
            }
            else
            {
                scanf("%d",&a);
                printf("%d\n",query(a));
            }
        }
    }
    return 0;
}

                             对点i来说，如果一个点是轻点，则记录所有与他相连的点到point[i]中

                                                  如果一个点是重点，则记录所有与他相连的重点到point[i]中