二分图的最大匹配
http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=474
description |
Farmer John completed his new barn just last week, complete with all the latest milking technology. Unfortunately, due to engineering problems, all the stalls in the new barn are different. For the first week, Farmer John randomly assigned cows to stalls, but it quickly became clear that any given cow was only willing to produce milk in certain stalls. For the last week, Farmer John has been collecting data on which cows are willing to produce milk in which stalls. A stall may be only assigned to one cow, and, of course, a cow may be only assigned to one stall.
Given the preferences of the cows, compute the maximum number of milk-producing assignments of cows to stalls that is possible.
|
input |
|
output |
|
sample_input |
|
sample_output |
4 |
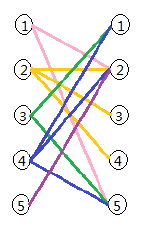
简单思路:这题的最大流模型不是那么明显了,我们首先根据样例画出题目的图如下:
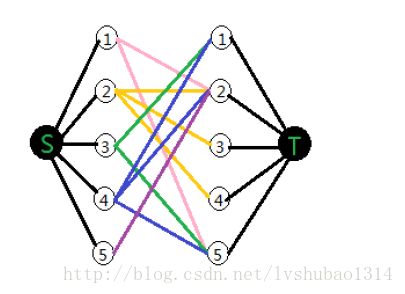
我们仔细的分析,题目要求最大的匹配数,也就是通过左边的点,从右边的点穿出,使得穿出的个数最多,每个点只能穿过一次,怎么看起来和最大流纳闷像呢?我们在图中价个源点和汇点看看:
没错,有了源点和汇点,源点到左边每个流量都是1,也就是只能通过一次,汇点也类似,而从左边的点到右边的点对应的边的边容量为1,就这样,这道题成功转换为最大流问题,建图后用最大流解决。
补充一句:所有二分图的最大匹配问题都可以通过类似得方法转化成最大流问题,用最大流解决,除非出题者邪恶了 T_T
#include <stdio.h>
#include <iostream>
using namespace std;
//--------------------------------------------------------
//--------------------------------------------------------
//最大流模板
const int oo=1e9;
const int mm=111111;
const int mn=999;
int node ,scr,dest,edge;
int ver[mm],flow[mm],next[mm];
int head[mn],work[mn],dis[mn],q[mn];
void prepare(int _node,int _scr,int _dest)
{
node=_node,scr=_scr,dest=_dest;
for(int i=0; i<node; ++i)
head[i]=-1;
edge=0;
}
void addedge(int u,int v,int c)
{
ver[edge]=v,flow[edge]=c,next[edge]=head[u],head[u]=edge++;
ver[edge]=u,flow[edge]=0,next[edge]=head[v],head[v]=edge++;
}
bool Dinic_bfs()
{
int i,u,v,l,r=0;
for(i=0; i<node; i++)
dis[i]=-1;
dis[q[r++]=scr]=0;
for(l=0; l<r; ++l)
{
for(i=head[u=q[l]]; i>=0; i=next[i])
{
if(flow[i]&&dis[v=ver[i]]<0)
{
dis[q[r++]=v]=dis[u]+1;
if(v==dest)
return 1;
}
}
}
return 0;
}
int Dinic_dfs(int u,int exp)
{
if(u==dest)
return exp;
for(int &i=work[u],v,tmp; i>=0; i=next[i])
if(flow[i]&&dis[v=ver[i]]==dis[u]+1&&(tmp=Dinic_dfs(v,min(exp,flow[i])))>0)
{
flow[i]-=tmp;
flow[i^1]=tmp;
return tmp;
}
return 0;
}
int Dinic_flow()
{
int i,ret=0,delta;
while(Dinic_bfs())
{
for(i=0; i<node; i++)
work[i]=head[i];
while(delta=Dinic_dfs(scr,oo))
ret+=delta;
}
return ret;
}
//----------------------------------------------------------
//----------------------------------------------------------
int main()
{
int n,m,u,v,c;
while(~scanf("%d%d",&n,&m))
{
prepare(n+m+2,0,n+m+1);
for(u=1;u<=n;++u)
{
addedge(scr,u,1);
scanf("%d",&c);
while(c--)
{
scanf("%d",&v);
addedge(u,n+v,1);
}
}
while(m)
addedge(n+m--,dest,1);
printf("%d\n",Dinic_flow());
}
return 0;
}