二分匹配
简单讲：
概念：
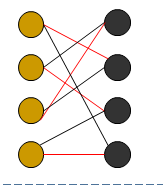
匹配：设G是一个图，若M中的边都是杆，并且任意两条边均不邻接，则称M为G的一个匹配。
最大匹配（边的最大独立集）：G的边数最多的匹配称为最大匹配。
点的最大独立集：设S是图G的顶点子集合。如果S中任意两个顶点在G中均不邻接，则称S是G的一个点独立集
最小点覆盖：找出最少的点，使得每条边至少和其中一个点连接。
最小边覆盖: 找出最少的边，使得每个点都有边与其相连
二分匹配：最大匹配：hdu 2063、1498
最小路径覆盖：poj 2226、1422、4160
最大独立集：hdu 1068、3829
最小点覆盖：hdu 1150、3360
最优匹配：hdu 2255
二分图最优匹配：对于二分图的每条边都有一个权（非负），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最优完备匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题）
先说一个定理：设M是一个带权完全二分图G的一个完备匹配，给每个顶点一个可行顶标(第i个x顶点的可行标用lx[i]表示，第j个y顶点的可行标用ly[j]表示)，如果对所有的边(i,j) in G,都有lx[i]+ly[j]>=w[i,j]成立(w[i,j]表示边的权)，且对所有的边(i,j) in M,都有lx[i]+ly[j]=w[i,j]成立，则M是图G的一个最优匹配。
Kuhn－Munkras算法（即KM算法）流程：
v (1)初始化可行顶标的值
v (2)用匈牙利算法寻找完备匹配
v (3)若未找到完备匹配则修改可行顶标的值
v (4)重复(2)(3)直到找到相等子图的完备匹配为止
KM算法主要就是控制怎样修改可行顶标的策略使得最终可以达到一个完美匹配，首先任意设置可行顶标（如每个X节点的可行顶标设为它出发的所有弧的最大权，Y节点的可行顶标设为0），然后在相等子图中寻找增广路，找到增广路就沿着增广路增广。而如果没有找到增广路呢，那么就考虑所有现在在匈牙利树中的X节点（记为S集合），所有现在在匈牙利树中的Y节点（记为T集合），考察所有一段在S集合，一段在not T集合中的弧，取 delta = min {l(xi)+l(yj)-w(xi,yj) , | xi in S, yj in not T} 。明显的，当我们把所有S集合中的l(xi)减少delta之后，一定会有至少一条属于(S, not T)的边进入相等子图，进而可以继续扩展匈牙利树，为了保证原来属于(S,T )的边不退出相等子图，把所有在T集合中的点的可行顶标增加delta。随后匈牙利树继续扩展，如果新加入匈牙利树的Y节点是未盖点，那么找到增广路，否则把该节点的对应的X匹配点加入匈牙利树继续尝试增广。
int n,sx[20],sy[20],lx[20],ly[20],match[20],w[20][20];
int dfs(int k)
{
int i;
sx[k]=1;
for(i=1;i<=n;i++)
{
if(!sy[i]&&w[k][i]==(lx[k]+ly[i]))
{
sy[i]=1;
if(!match[i]||dfs(match[i]))
{
match[i]=k;
return 1;
}
}
}
return 0;
}
void KM()
{
int i,j,k,min;
memset(ly,0,sizeof(ly));
for(i=1;i<=n;i++)
{
lx[i]=w[i][1];
for(j=2;j<=n;j++)
{
if(lx[i]<w[i][j])
lx[i]=w[i][j];
}
}
memset(match,0,sizeof(match));
for(i=1;i<=n;i++)
{
while(1)
{
memset(sx,0,sizeof(sx));
memset(sy,0,sizeof(sy));
if(dfs(i))break;
min=1000000000;
for(j=1;j<=n;j++)
{
if(sx[j])
{
for(k=1;k<=n;k++)
if(!sy[k])
min=min<(lx[j]+ly[k]-w[j][k])?min:(lx[j]+ly[k]-w[j][k]);
}
}
for(j=1;j<=n;j++)
{
if(sx[j])lx[j]-=min;
if(sy[j])ly[j]+=min;
}
}
}
}
/*****************************************************************************************************************************/
二分图相关问题
二分图最大匹配
二分图最小覆盖
二分图最大独立集
二分图最小路径覆盖
二分图最优匹配
稳定婚姻问题
二分图定义及判定
定义：二分图中，顶点可以分为两个集合X和Y，每一条边的两个顶点都分别位于X和Y集合中
判定：利用BFS或者DFS进行黑白染色，共享一边的两点异色，检查是否存在矛盾
图G为二分图的充要条件是图中不含奇环
定义：匹配是二分图中边的集合，
且集合中的任意两条边没有公共点，包含边数最多的匹配就是最大匹配
匈牙利算法
概念：交错路
对于一个匹配
M
，如果能找到一条奇数长度的路，使得路的第一、三、五
……
边不属于
M
，而第二、四、六
……
边属于
M
，那么这条路叫做交错路。
交错路可以“增广”，即通过适当修改得到更大的匹配。
交错路增广示例
(1-2-3-4-5-6-7-8)
定理：一个匹配为最大匹配当且仅当匹配中不存在交错路
证明相当繁琐,具体参见组合数学
可以利用
BFS
或者
DFS
实现寻找交错路
匈牙利算法的实现还依赖于一个很重要的定理：如果从一个点出发，没有找到增广路径，那么无论再从别的点出发找到多少增广路径来改变现在的匹配，从这个点出发都永远找不到增广路径。
Why ？
Why ？
AV0V1V2V3…….B
如果是V0或V2或…..的匹配的改变导致找到交错路，那么改变的这点也存在于交错路中，那么在改变之前就应该找到交错路
DFS实现
int find(int k) {
for (每个与k相邻的点j)
if (cover[j] == FALSE) {
q = link[j];
link[j] = k;
cover[j] = TRUE;
if (q == -1 || find(q) == 1) return 1;
link[j] = q;
}
return 0;
}
work() {
link[ ]数组初始化为-1
for (i = 0 ; i < m ; i++) {
cover[ ]数组初始化为FALSE;
find(i);
}
}
简要说明：
find
函数用于判断从
k
点开始是否能够找到一条交错路。对于每个可以与
k
匹配的顶点
j
，假如它未被匹配，交错路就已经找到；假如
j
已与某顶点
x
匹配，那么只需调用
find(x)
来求证
x
是否可以与其它顶点匹配，如果返回
true
的话，仍可以使
j
与
k
匹配；这就是一次
DFS
。每次
DFS
时，要标记访问到的顶点（
cover[j]=true
），以防死循环和重复计算。
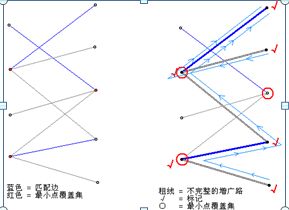
二分图最小覆盖
图的覆盖：寻找一个点集，使得图中每一条边至少有一点在该点集中
最小覆盖
如何构造一组最小覆盖？
求得最大匹配M后，图中已经不存在交错路。从右边未匹配的点开始，以寻找交错路的方式扩展节点，并标记路过的节点。取右边未标记的节点，左边标记的节点，则构成一组最小覆盖。
证明
1，所取节点数=|M| .右边未匹配的点肯定被标记了，左边未匹配的点不可能被标记（否则找到了交错路），一条匹配边的左端点被标记，那么右端点也肯定被标记，所以所取节点恰覆盖一条匹配边
3，最小（why？）
二分图最大独立集
图的独立集：寻找一个点集，其中任意两点在图中无对应边
二分图的最大独立集=图的点数-最大匹配数
可以这样理解，在总的点集中，去掉最少的点，使得剩下的点相互之间没有边。用最少的点去覆盖所有的边，也就是最小覆盖。
二分图的最大独立集
=
图的点数
-
最大匹配数
例：
骑士问题
一个n*n的棋盘上,有一些单位小方格不能放置骑士。求出最多可以放置几个相互不攻击的骑士
X
代表攻击范围，
S
代表骑士
分析
对棋盘染色，设方格的坐标为
(
x,y
)
，
x
和
y
同奇偶的方格对应
X
集合，不同奇偶的对应
Y
集合。由于骑士沿着“日”字形路线攻击，所以每个攻击肯定是处于
X
集合和
Y
集合之间，而不可能在两个集合内部。
显然，转化后变为求二分图的最大独立集
二分图的最小路径覆盖
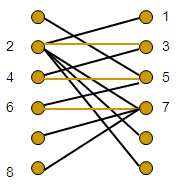
最小路径覆盖问题：用尽量少的不相交简单路径覆盖有向无环图的所有顶点
将每个顶点分为两个，分别在X集合和Y集合中，如果存在有向边(a,b)，对应在二分图中有（Xa,Yb）
最小路径数=节点数-最大匹配
简单解释：
原图的路径覆盖和新图的匹配间有对应关系：
每条覆盖边都是匹配中的一条边，且只有路径的最后一个点没有被匹配上。
路径要求不能相交，恰好对应于匹配中两匹配边不能有公共端点。
于是求最大匹配后，不能被匹配上的点，即是路径的最后一个点。有多少个不能被匹配的点，就有多少条路径存在。
路径数
=
原点数－匹配边数。因此我们使匹配边数最大，即是使路径数最小。
例
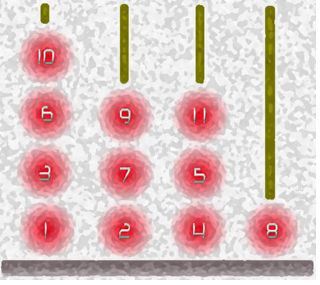
Hanoi Tower Troubles Again! (OIBH Contest)
ZOJ 1239
点击打开链接
题目大意：给定柱子数
N
，按编号从小到大放球，要求：如果该球不在最底数，则该球和它下面一个球的编号之和必须为完全平方数。
问对于给定的
N
，最多能放多少球上去。
N<=50
分析：
放
K
个球至少需要几根柱子？
每个球看做是一个节点，对于球a,b（a<b），如果a+b是完全平方数，那么有一条a指向b的边，由于a总是小于b，显然所建图无环。
每根柱子相当于一条路径，而且每个球只能位于一根柱子上，所以保证了路径不会相交，至此，问题转化为最小路径覆盖
能够放的球的数目是随着柱子数单调递增的。
根据答案的单调性，我们可以通过二分答案解，将每次二分出的答案和N做比较，最后得出答案
二分图最优匹配
又称带权最大匹配。
二分图的每条边带有权值。求一个匹配使得匹配边上的权值和最大。
一般X和Y集合顶点个数相同，最优匹配也是一个完备匹配，即每个顶点都被匹配。如果个数不相等，可以通过补点加0边实现转化。
最小？
基本概念：可行顶标和相等子图
可行顶标：
L
是一个关于结点的函数，
L(x)
是顶点
x
对应的顶标值。可行顶标对于图中的每条边
(
x,y
)
都有
L(x)+L(y)>=w(
x,y
)
相等子图：只包含
L(x)+L(y)=w(
x,y
)
的边的子图
定理：如果一个相等子图中包含完备匹配，那么这个匹配就是最优匹配
算法流程
设顶点Xi的顶标为a[i]，顶点Yi的顶标为b[i]
ⅰ.
初始时，
a[
i
]
为与
Xi
相关联的边的最大权值，
b[j]=0
，保证
a[
i
]+b[j]>=w(
i,j
)
成立
ⅱ.
当相等子图中不包含完备匹配时，就适当修改顶标以扩大相等子图，直到找到完备匹配为止
ⅲ.
修改顶标的方法
当从
Xi
寻找交错路失败后，得到一棵交错树，它的所有叶子节点都是
X
节点，对交错树中
X
顶点的顶标减少
d
值，
Y
顶点的顶标增加
d
值，对于图中所有的边
(
i,j
)
，可以看到
i
和
j
都不在交错树中，边
(
i,j
)
仍然不属于相等子图
i
和
j
都在交错树中，边
(
i,j
)
仍然属于相等子图
i
不在交错树中，
j
在交错树中，
a[
i
]+b[j]
扩大，边
(
i,j
)
不属于相等子图
为了使
a[
i
]+b[j]>=w(
i,j
)
始终成立
,
且至少有一条边加入到相等子图中
,d=min{a[
i
]+b[j]-w(
i,j
)},
i
在交错树中
,j
不在交错树中
时间复杂度
:
需要找
O(n)
次增广路，每次增广最多需要修改
O(n)
次顶标，每次修改顶标时枚举边来求
d
值，复杂度为
O(n2),
总的复杂度为
O(n4).
简单优化可以降低到
O(n3),
每个
Y
顶点一个“松弛量”函数
slack
，每次开始找增广路时初始化为无穷大。在寻找增广路的过程中，检查边
(
i,j
)
时，如果不在相等子图中，则让
slack[j]
变成原值与
A[
i
]+B[j]-w[
i,j
]
的较小值。这样，在修改顶标时，取所有不在交错树中的
Y
顶点的
slack
值中的最小值作为
d
值即可。但还要注意一点：修改顶标后，要把所有的
slack
值都减去
d
。
例
丘比特的烦恼
丘比特选择了一组数目相等的男女，感应到他们互相之间的缘分大小，射出神箭，使他们相爱。请帮助丘比特选择最好的方法，使得每个人被射中一次，且被射中的每一对情侣的缘分总和最大。
分析
建图很明显，“男左女右”，二分图中的边为对应在男女集合中互相缘分大小的和。
边建立完毕后，剩下的就是最优二分图匹配了
稳定婚姻
完备婚姻：
N
位男士和
N
位女士，组成
N
对配偶，每位男士按偏爱程度对
N
位女士排序，每位女士对
N
位男士也进行排序。
如果存在两对配偶，女士
A
和男士
a
，女士
B
和男士
b
，使得
A
更偏爱
b
而非
a
，且
b
更偏爱
A
而非
B
，那么就称这个完备婚姻是不稳定的
延迟认可算法
是否总是存在稳定婚姻？
延迟认可算法
初始每位女士处于未匹配状态。
当存在未匹配女士时
该女士在所有未拒绝过她的男士中选择她最喜欢的男士作为配偶
男士在所有选择他的女士中选择他最喜欢的作为配偶