hdu4576 Robot

Robot

Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 359 Accepted Submission(s): 139

Problem Description

Michael has a telecontrol robot. One day he put the robot on a loop with n cells. The cells are numbered from 1 to n clockwise.



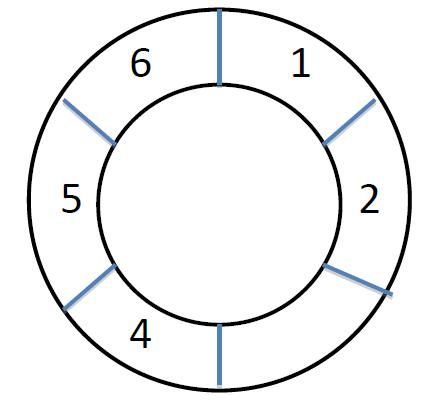
At first the robot is in cell 1. Then Michael uses a remote control to send m commands to the robot. A command will make the robot walk some distance. Unfortunately the direction part on the remote control is broken, so for every command the robot will chose a direction(clockwise or anticlockwise) randomly with equal possibility, and then walk w cells forward.
Michael wants to know the possibility of the robot stopping in the cell that cell number >= l and <= r after m commands.

Input

There are multiple test cases.
Each test case contains several lines.
The first line contains four integers: above mentioned n(1≤n≤200) ,m(0≤m≤1,000,000),l,r(1≤l≤r≤n).
Then m lines follow, each representing a command. A command is a integer w(1≤w≤100) representing the cell length the robot will walk for this command.
The input end with n=0,m=0,l=0,r=0. You should not process this test case.

Output

For each test case in the input, you should output a line with the expected possibility. Output should be round to 4 digits after decimal points.

Sample Input

   
   
   
   

    
    
    
    3 1 1 2
1
5 2 4 4
1
2
0 0 0 0
   
   
   
   

Sample Output

   
   
   
   

    
    
    
    0.5000
0.2500
   
   
   
   
   
   
   
   

    
    
    
    这题也是re了不知道多少次啊，题意还是很简单的，刚开始以为是搜索啊什么的，后来发现，不用考虑最后，注意，一定要一边加，一边除２，那么最后，不就是结果了么，因为，数据是太大了！只需要用前一个状态，左右走几步就可以推出下一个状态！这样，用dp，就可以过了啊！
   
   
   
   
   
   
   
   

    
    
    
    
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
#define MAXN 2200
double prime[MAXN][2];
int mand;
int main()
{

    int n,m,l,r,flag,minx,maxx,i,j;
    double sum;
    while(scanf("%d%d%d%d",&n,&m,&l,&r)!=EOF)
    {
        if(n==0&&m==0&&l==0&&r==0)
        break;
        flag=1;
       for(j=0;j<=n;j++)
            prime[j][flag]=0;
        prime[0][1]=1;
       for(i=0;i<m;i++)
        {

            flag=flag^1;
            for(j=0;j<=n;j++)
                prime[j][flag]=0;
            scanf("%d",&mand);
            for(j=0;j<n;j++)
            {
                if(prime[j][flag^1]==0)
                continue;
                minx=j-mand;
                if(minx<0)
                    minx=(n+(minx)%n)%n;
                maxx=j+mand;
                if(maxx>=n)
                {
                    maxx=maxx%n;
                }
                prime[maxx][flag]+=prime[j][flag^1]*0.5;
                prime[minx][flag]+=prime[j][flag^1]*0.5;
             }
        }

        for(sum=0,i=l-1;i<r;i++)
        {
            sum+=prime[i][flag];
        }
        printf("%.4f\n",sum);
    }
    return 0;
}