归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
归并操作的工作原理如下:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。
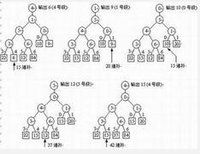
初始状态: [6] [202] [100] [301] [38] [8] [1] 比较次数
i=1 [6 202 ] [ 100 301] [ 8 38] [ 1 ] 3
i=2 [ 6 100 202 301 ] [ 1 8 38 ] 4
i=3 [ 1 6 8 38 100 202 301 ] 4
总计: 11次
时间复杂度为O(nlogn) 这是该算法中最好、最坏和平均的时间性能。
空间复杂度为 O(n)
比较操作的次数介于(nlogn) / 2和nlogn - n + 1。
赋值操作的次数是(2nlogn)。归并算法的空间复杂度为:0 (n)
归并排序比较占用内存,但却效率高且稳定的算法。
#include<iostream.h>
void Merge(int r[],int r1[],int s,int m,int t)
{
int i=s;int j=m+1;int k=s;
while(i<=m&&j<=t)
{
if(r<=r[j])r1[k++]=r[i++];
else r1[k++]=r[j++];
}
if(i<=m)
while(i<=m) r1[k++]=r[i++];
else while(j<=t)
r1[k++]=r[j++];
for(int l=0;l<8;l++)
r[l]=r1[l];
}
void MergeSort(int r[],int r1[],int s,int t)
{
if(s==t)r1[s]=r[s];
else
{
int m=(s+t)/2;
MergeSort(r,r1,s,m);
MergeSort(r,r1,m+1,t);
Merge(r1,r,s,m,t);
}
}
void main()
{
int r[8]={10,3,5,1,9,34,54,565},r1[8];
MergeSort(r,r1,0,7);
for(int q=0;q<8;q++)
cout<<" "<<r[q];
}
public static int[] mergeSort(int[] data1,int[] data2)
{
int[] temp=new int[data1.length+data2.length];
int i=0,j=0,iter=0;
for(;i<data1.length&&j<data2.length;)
{
if(data1<=data2[j])
{
temp[iter]=data1;
iter++;
i++;
}
else
{
temp[iter]=data2[j];
iter++;
j++;
}
}
for(;i<data1.length;i++,iter++)
{
temp[iter]=data1;
}
for(;j<data2.length;j++,iter++)
{
temp[iter]=data2[j];
}
return temp;
}
归并排序有两种实现方法:自底向上和自顶向下,算法实现如下:
1.自底向上算法
#include <stdio.h>
#include <time.h>
void Merge(int *a,int low,int mid,int high)
{
int i = low,j = mid + 1,k = 0;
int *temp = (int *)malloc((high - low + 1)*sizeof(int));
while(i <= mid && j <= high)
a < a[j] ? (temp[k++] = a[i++]):(temp[k++] = a[j++]);
while(i <= mid)
temp[k++] = a[i++];
while(j <= high)
temp[k++] = a[j++];
memcpy(a + low,temp,(high -low + 1)*sizeof(int));
free(temp);
}
void MergeSort(int *a,int n)
{
int length;
for(length = 1;length < n;length *= 2)
{
int i;
for( i = 0;i + 2*length - 1 <= n - 1;i += 2*length)
Merge(a,i,i+length-1,i+2*length -1);
if(i + 2*length - 1 <= n - 1)//尚有两个子文件,其中后一个长度小于length
Merge(a,i,i +2* length -1,n - 1);
}
}
int main()
{
int n;
cin >> n;
int *data = new int[n];
if(!data) exit(1);
int k = n;
while(k --)
{
cin >> data[n-k-1];
}
clock_t s = clock();
MergeSort(data, n);
clock_t e = clock();
k = n;
while(k --){
cout << data[n-k-1] << ' ';
}
cout << endl;
cout << "the algrothem used " << e-s << " miliseconds."<< endl;
delete data;
return 0;
}
void Merge(int r[],int r1[],int s,int m,int t)
{
int i=s;int j=m+1;int k=s;
while(i<=m&&j<=t)
{
if(r<=r[j])r1[k++]=r[i++];
else r1[k++]=r[j++];
}
while(i<=m) r1[k++]=r[i++];
while(j<=t)
r1[k++]=r[j++];
for(int l=0;l<8;l++)
r[l]=r1[l];
}
void MergeSort(int r[],int r1[],int s,int t)
{
if(s==t)r1[s]=r[s];
else{
int m=(s+t)/2;
MergeSort(r,r1,s,m);
MergeSort(r,r1,m+1,t);
Merge(r1,r,s,m,t);
}
}
折叠非递归算法(C++)
#include <iostream>
#include <ctime>
#include <cstring>
using namespace std;
/** 将a开头的长为length的数组和b开头长为right的数组 合并 n为数组长度,用于最后一组 */
void Merge(int* data, int a, int b, int length, int n){
int right;
if(b+length-1 >= n-1) right = n-b;
else right = length;
int* temp = new int[length+right];
int i = 0, j = 0;
while(i<=length-1&&j<=right-1){
if(data[a+i] <= data[b+j]){
temp[i+j] = data[a+i]; i++; }
else{ temp[i+j] = data[b+j]; j++; }
}
if(j == right){// a中还有元素,且全都比b中的大,a还未使用
memcpy(data+a+i+j, data+a+i,(length-i)*sizeof(int));
}
memcpy(data+a, temp, (i+j)*sizeof(int) );
delete temp;
}
void MergeSort(int* data, int n){
int step = 1;
while(step < n){
for(int i = 0; i <= n-step-1; i += 2*step)
Merge(data, i, i+step, step, n);
// 将i和i+step这两个有序序列进行合并
// 序列长度为step
// 当i以后的长度小于或者等于step时,退出
tep *= 2;
}
}
int main(){
int n;
cin >> n;
int *data = new int[n];
if(!data) exit(1);
int k = n;
while(k --){
cin >> data[n-k-1];
}
clock_t s = clock();
MergeSort(data, n);
clock_t e = clock();
k = n;
while(k --){
cout << data[n-k-1] << ' ';
}
cout << endl;
cout << "the algrothem used " << e-s << " miliseconds."
lt;< endl;
delete data;
return 0; }