大话快排 和 归排的渊源

一：起因

（1）包括冒泡算法、快排算法、插入排序算法等；还有基于外部排序的归并排序（以二路归并排序为例 ）

但是基本上在一个数量级上；

（2）

mergesort (归并排序) 可以应用在外部排序，这与基于内存的quicksort(快速排序)略有不同，他们的算法复杂度都可以达到O(nlogn)

（3)mergesort 是稳定的排序算法，需要额外的空间开销O(n)；quicksort 是非稳定的排序算法，额外的空间开销O(1)；两者的核心思想都来源与分支的策略（divide and conquer）,一个是merge 过程，一个是partition过程。

二：详解

（1）归并排序

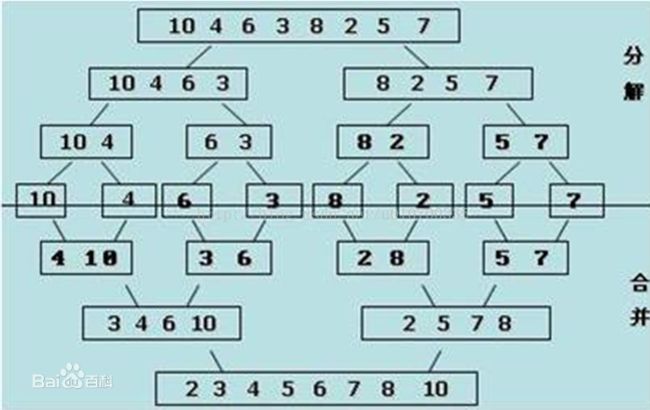
归并操作的工作原理如下：

第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列（或者只申请一次，多次使用空间）

第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置

第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

重复步骤3直到某一指针超出序列尾

第四步：将另一序列剩下的所有元素直接复制到合并序列尾   ----- 分治策略

图解：

（2）代码

struct node
{
	int key;
	int num;
}n[N],t[N];
void merge(struct node s[], int low, int mid, int high, struct node temp[])
{// 相当于合并 同一个数组 中的两段有序的序列
	int i,j,k;
	i=low,j=mid+1,k=0;
	while (i<=mid&&j<=high)
	{
		if (s[i].key<=s[j].key)
		{
			temp[k].key = s[i].key;
			i ++;
			k ++;
		}
		else
		{
			temp[k].key = s[j].key;
			j ++;
			k ++;
		}
	}// 剩下的添加到末位
	while (i<=mid)
	{
		temp[k++].key = s[i++].key;//和if里面一样的效果
	}
	while (j<=high)
	{
		temp[k++].key = s[j++].key;
	}
<span style="white-space:pre">	</span>// 把temp里排序好的放到原始数组中
	for (i=0; i<k; i++)
	{
		s[low+i] = temp[i];
	}
}

void merge_sort(struct node s[],int low,int high,struct node temp[])
{
	int mid;	
	if (low < high)
	{
		mid = low + (high-low)/2;
		merge_sort(s,low,mid,temp);//左边分割 、归并排序
		merge_sort(s,mid+1,high,temp);//右边分割、归并排序
		merge(s,low,mid,high,temp);//
	}
}

小结：可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

（3）快速排序

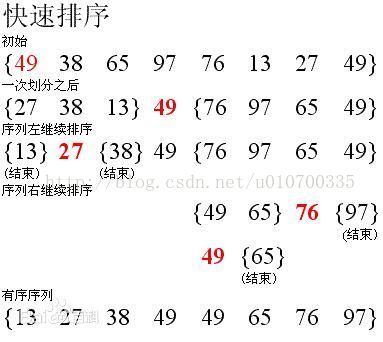
快速排序（Quicksort）是对冒泡排序的一种改进。由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。 ----- 分治策略

每一趟快速排序的算法是 partition算法： （而整个quicksort 是根据每一次返回的part下标值，进行下一轮的partition，直到low >= high）
1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；
2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；
4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；
5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

图解：

（4）代码

int paritition(data b[], int left, int right)//从小到大  
{  
    if(left < right)  
    {  
        int key = b[left].key;  
        int low = left;  
        int high = right;  
        while(low < high)  
        {  
            while(low < high && b[high].key >= key)  
            {  
                high--;  
            }  
            b[low].key = b[high].key;//若是没有找到比key 小的（即由于low = high 而退出循环），  
            //则这句话的意思是把自己赋值给自己。  
  
            while(low < high && b[low].key <= key)  
            {  
                low++;  
            }  
            b[high].key = b[low].key;//若是没有找到比key 大的（即由于low = high 而退出循环），  
            //则这句话的意思……（分情况：当上面的找到比key小的了，则移动；当上面也没有找到，则自己赋值给自己）。  
        }  
  
        b[low].key = key;  
        return low;
    }  
    return 0;  
}

分治算法

void quick_sort(int s[], int l, int r)
{
	if (l < r)
    {
		int i = partition(s, l, r);//partition 算法
		quick_sort1(s, l, i - 1); // 递归调用 
		quick_sort1(s, i + 1, r);
	}
}