关于图像的插值运算

 一. 图像缩放的双线性内插值算法的原理解析 

图像的缩放很好理解,就是图像的放大和缩小。传统的绘画工具中,有一种叫做“放大尺”的绘画工具，画家常用它来放大图画。当然，在计算机上，我们不再需要用放大尺去放大或缩小图像了，把这个工作交给程序来完成就可以了。下面就来讲讲计算机怎么来放大缩小图象；在本文中，我们所说的图像都是指点阵图，也就是用一个像素矩阵来描述图像的方法，对于另一种图像：用函数来描述图像的矢量图，不在本文讨论之列。
越是简单的模型越适合用来举例子，我们就举个简单的图像：3X3 的256级灰度图，也就是高为3个象素，宽也是3个象素的图像，每个象素的取值可以是 0－255，代表该像素的亮度，255代表最亮，也就是白色，0代表最暗，即黑色 。假如图像的象素矩阵如下图所示（这个原始图把它叫做源图，Source）：
234   38    22
67     44    12
89     65    63

这个矩阵中，元素坐标(x,y)是这样确定的，x从左到右，从0开始，y从上到下，也是从零开始，这是图象处理中最常用的坐标系，就是这样一个坐标：

  ----------------------＞X
  |
  |
  |
  |
  |
∨Y

如果想把这副图放大为 4X4大小的图像，那么该怎么做呢？那么第一步肯定想到的是先把4X4的矩阵先画出来再说，好了矩阵画出来了，如下所示，当然，矩阵的每个像素都是未知数，等待着我们去填充（这个将要被填充的图的叫做目标图,Destination）：
?        ?        ?       ?
?        ?        ?       ?
?        ?        ?       ?
?        ?        ?       ? 
               
        然后要往这个空的矩阵里面填值了，要填的值从哪里来来呢？是从源图中来，好，先填写目标图最左上角的象素，坐标为（0，0），那么该坐标对应源图中的坐标可以由如下公式得出：                                      
srcX=dstX* (srcWidth/dstWidth) , srcY = dstY * (srcHeight/dstHeight)
好了，套用公式，就可以找到对应的原图的坐标了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0)
,找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。

接下来,如法炮制,寻找目标图中坐标为(1,0)的象素对应源图中的坐标,套用公式:
(1*0.75,0*0.75)=>(0.75,0)
结果发现,得到的坐标里面竟然有小数,这可怎么办?计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法（也可以采用直接舍掉小数位的方法），把非整数坐标转换成整数，好，那么按照四舍五入的方法就得到坐标（1，0），完整的运算过程就是这样的：
(1*0.75,0*0.75)=>(0.75,0)=>(1,0)
那么就可以再填一个象素到目标矩阵中了，同样是把源图中坐标为(1,0)处的像素值38填入目标图中的坐标。
         
依次填完每个象素，一幅放大后的图像就诞生了，像素矩阵如下所示：
234    38     22     22  
67      44     12     12  
89      65     63     63  
89      65     63     63  

这种放大图像的方法叫做最临近插值算法，这是一种最基本、最简单的图像缩放算法，效果也是最不好的，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真；效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真，比如，当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候，采用了四舍五入的方法，直接采用了和这个浮点数最接近的象素的值，这种方法是很不科学的，当推得坐标值为 0.75的时候，不应该就简单的取为1，既然是0.75，比1要小0.25 ，比0要大0.75 ,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的，这样才能达到更好的缩放效果。双线型内插值算法就是一种比较好的图像缩放算法，它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值，因此缩放效果比简单的最邻近插值要好很多。

双线性内插值算法描述如下:
　　对于一个目的像素，设置坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：

　　f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)                          公式1

其中f(i,j)表示源图像(i,j)处的的像素值，以此类推。

比如，象刚才的例子，现在假如目标图的象素坐标为（1，1），那么反推得到的对应于源图的坐标是（0.75 , 0.75）, 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素（1，1）的取值不能够由这个虚拟象素来决定，而只能由源图的这四个象素共同决定：（0，0）（0，1）（1，0）（1，1），而由于（0.75,0.75）离（1，1）要更近一些，那么（1,1）所起的决定作用更大一些，这从公式1中的系数uv=0.75×0.75就可以体现出来，而（0.75,0.75）离（0，0）最远，所以（0，0）所起的决定作用就要小一些，公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点；

最邻近插值和双向性内插值缩放图片的效果对比：

      原始图片

       最邻近插值放大图片

    双线型内插值放大图片

二. 双线性插值的图像缩放算法的研究与实现

一、引言

数字图像处理的对象因其涉及到社会的各个领域，倍受到越来越多的关注，而图像缩放作为数字图像处理中的基本操作尤为重要，在社会的很多领域都需要对图像进行放大和缩小。利用VC++的MFC类库中的StretchBlt函数可以很容易的实现图像放大和缩小，但是当放大或缩小的比率比较大时就容易出现失真现象，因此必须进行改进。本文提出了一种双线性插值算法，用以改进图像的缩放质量。

二、空间变换

    图像的空间变换，也称几何变换或几何运算，包括图像的平移、旋转、镜像变换、转置、缩放等。几何运算可改变图像中各物体之间的空间关系，这种运算可以被看成是将各物体在图像内移动。

   空间变换可如下表示：设(u，v)为源图像上的点，(x,y)为目标图像上的点，则空间变换就是将源图像上(u，v)处的颜色值与目标图像上(x，y)处的颜色对应起来。

(u，v) ?----------------à (x，y)

并具有以下关系：

x=X(u,v)，y=Y(u,v)   (即由(u，v)计算对应点(x，y)  )    (1.1)

或

u=U(x，y)，v=V(x,y)  (即由(x，y)反求对应点(u，v)  )(1.2)其中X(u,v)、Y(u,v)、U(x，y)、V(x,y)均为变换。由(1.1)对应的变换称作向前映射法也叫像素移交法，而由(1.2)对应的变换称作向后映射法也叫像素填充法，向后映射法是向前映射法的逆。

对于向前映射法来说，由于许多输入像素可能映射到输出图像的边界之外，所以，向前映射法有些浪费，而且每个输出像素的灰度值可能要由许多输入像素的灰度值来决定，因此要涉及多次运算。如果空间变换中包括缩小处理，则会有四个以上的输入像素来决定输出像素的灰度值；如果含有放大处理，则一些输出像素可能被漏掉。而向后映射算法是逐像素、逐行地产生输出图像。每个像素的灰度级由最多四个像素参与的插值所惟一确定，虽然向后映射法比向前映射法要复杂，但是向后映射法对于一般的应用却具有更为现实的意义。本文就是采取了向后映射法来实现图像缩放的。

三．双线性插值

   最简单的插值算法是最邻近插值，也称为零阶插值。它输出的像素灰度值就等于距离它映射到的位置最近的输入像素的灰度值，最邻近插值算法简单，在许多情况下都能得到令人满意的结果，但是当图像中包含像素之间灰度级有变化的细微结构时，最邻近算法会在图像中产生人为加工的痕迹。双线性插值算法计算量比零阶插值大，但缩放后图像质量高，不会出现像素值不连续的情况，这样就可以获得一个令人满意的结果。

   双线性插值是利用了需要处理的原始图像像素点周围的四个像素点的相关性，通过双线性算法计算得出的。对于一个目的坐标，通过向后映射法得到其在原始图像的对应的浮点坐标（i+u，j+v），其中i，j均为非负整数，u，v为[0，1]区间的浮点数，则这个像素的值 f(i+u，j+v) 可由原图像中坐标为 (i，j)、(i+1，j)、(i，j+1)、(i+1，j+1)所对应的周围四个像素的值决定，即：f(i+u，j+v) =(1-u)×(1-v) ×f(i，j)+(1-u) ×v×f(i,j+1)+u×(1-v) ×f(i+1,j)+u×v×f(i+1,j+1)，其中f(i，j)表示源图像(i，j)处的像素值，以此类推，这就是双线性内插值法。

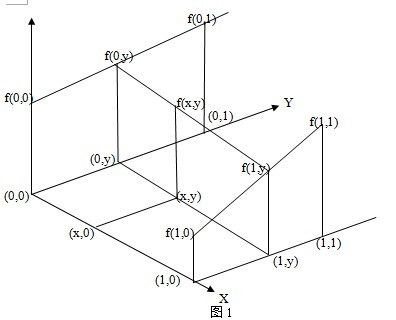
如图1所示，已知(0,0)、(0,1)、(1,0)、(1,1)四点的灰度，可以由相邻像素的灰度值f(0,0)和f(1,0) 在X方向上线性插值求出(x,0)的灰度f(x,0)，由另外两个相邻像素f(0,1)和f(1,1)在X方向上线性插值可求出(x,1)的灰度f(x,1),最后由f(x,0)、f(x,1)在Y方向上进行线性插值就可以得到(x,y)的灰度f(x,y)。

四.算法

 

1.算法

 

假设原始图像大小为size=m×n，其中m与n分别是原始图像的行数与列<数。若图像的缩放因子是t（t>0），则目标图像的大小size=t×m×t×n。对于目标图像的某个像素点P（x，y）通过P*1/t可得到对应的原始图像坐标P’( x1，y1),其中x1=x/t，y1=y/t，由于x1，y1都不是整数所以并不存在这样的点，这样可以找出与它相邻的四个点的灰度f1、f2、f3、f4，使用双线性插值算法就可以得到这个像素点P’(x1，y1)的灰度，也就是像素点P（x，y）的灰度。

一个完整的双线性插值算法可描述如下：

（1）       通过原始图像和比例因子得到新图像的大小，并创建新图像。

（2）       由新图像的某个像素（x，y）映射到原始图像(x’，y’)处。

（3）       对x’,y’取整得到（xx，yy）并得到(xx，yy)、(xx+1，yy)、（xx，yy+1）和（xx+1，yy+1）的值。

（4）       利用双线性插值得到像素点(x，y)的值并写回新图像。

（5）       重复步骤（2）直到新图像的所有像素写完。

2．核心代码

//函数名Bilinear

//参数float k

//返回值无

//作用利用双线性插值来实现图像缩放

void CChildView::Bilinear(float k)

{  

    int nBpp=m_imPicture .GetBPP ();   

    int widthNew,heightNew;//新图像的宽度和高度

    float widthScale=(float)(1.0/k),heightScale=(float)(1.0/k);

    float xx,yy;

    int a,b;

    int rr,gg,bb;//保存R、G、B分量

    //得到新图像的宽度和高度

    widthNew=(int)(m_imPicture .GetWidth ()*k);

    heightNew =(int)(m_imPicture .GetHeight ()*k);

    //利用新图像的宽度和高度来创建新图像

    m_imNewPicture .Destroy ();

    m_imNewPicture .Create (widthNew ,heightNew ,nBpp);

    //得到新、老图像的每行的字节数

    int nPitch=m_imPicture .GetPitch ();

    int nPitchNew=m_imNewPicture .GetPitch ();

    //得到新、老图像的数据指针

    LPBYTE pBitsNew=(LPBYTE)m_imNewPicture .GetBits ();

    LPBYTE pBits=(LPBYTE)m_imPicture .GetBits ();  

    if(m_imPicture.GetBPP ()!=24){

        MessageBox ("必须是24位图像或8位图像");

        m_imNewPicture .Destroy ();

        Invalidate();

        return ;

    }  

    for(int x=(int)k;x<widthNew -k;x++){

        for(int y=(int)k;y<heightNew -k;y++){

            xx=x*widthScale ;

            yy=y*heightScale ;

            if(xx<=1e-8){

                xx=0;

            }

            if(xx>m_imPicture .GetWidth ()-2)

                xx=(float)(m_imPicture .GetWidth ()-2);

            if(yy<=1e-8)

                yy=0;

            if(yy>m_imPicture .GetHeight ()-2)

                yy=(float)(m_imPicture .GetHeight ()-2);

            a=(int)xx;

            b=(int)yy;         

            //分别得到对应像素的R、G、B值并用双线性插值得到新像素的R、G、B值

            int r11,r12,r21,r22;

            r11=*(pBits+b*nPitch+3*a+2);

            r12=*(pBits+b*nPitch+3*(a+1)+2);

            r21=*(pBits+(b+1)*nPitch+3*a+2);

            r22=*(pBits+(b+1)*nPitch+3*(a+1)+2);

            rr=(int)(r11*(a+1-xx)*(b+1-yy)+r12*(a+1-xx)*(yy-b)

                +r21*(xx-a)*(b+1-yy)+r22*(xx-a)*(yy-b));

 

            int g11,g12,g21,g22;

            g11=*(pBits+b*nPitch+3*a+1);

            g12=*(pBits+b*nPitch+3*(a+1)+1);

            g21=*(pBits+(b+1)*nPitch+3*a+1);

            g22=*(pBits+(b+1)*nPitch+3*(a+1)+1);

            gg=(int)(g11*(a+1-xx)*(b+1-yy)+g12*(a+1-xx)*(yy-b)

                +g21*(xx-a)*(b+1-yy)+g22*(xx-a)*(yy-b));

 

            int b11,b12,b21,b22;

            b11=*(pBits+b*nPitch+3*a);

            b12=*(pBits+b*nPitch+3*(a+1));

            b21=*(pBits+(b+1)*nPitch+3*a);

            b22=*(pBits+(b+1)*nPitch+3*(a+1));

            bb=(int)(b11*(a+1-xx)*(b+1-yy)+b12*(a+1-xx)*(yy-b)

                +b21*(xx-a)*(b+1-yy)+b22*(xx-a)*(yy-b));

            //将得到的新R、G、B值写到新图像中          

            *(pBitsNew +y*nPitchNew +x*3)=min(255,bb);

            *(pBitsNew +y*nPitchNew +x*3+1)=min(255,gg);

            *(pBitsNew +y*nPitchNew +x*3+2)=min(255,rr);

        }      

    }      

    m_imPicture .Destroy ();

    Invalidate ();

}

五．结语

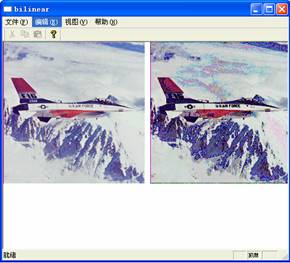
   本文介绍了一种利用双线性插值来实现图像缩放的算法，通过图2可以看到这种算法和传统的利用StretchBlt来实现图像缩放相比具有很大的改善。StretchBlt实现的图像具有很大的失真，并且随着缩小的比率越大失真也越严重；而双线性插值算法则很好地解决了这个问题，可以得到很高的清晰度，这种方法可以广泛应用在图像变形、计算机动画、计算机辅助设计等领域。所附源代码在VC++.NET 2003下编译通过。

图2

注：左图是利用本文介绍的双线性插值算法缩小一倍得到图像，右图是利用StretchBlt缩小一倍得到图像。