poj 2516 Minimum Cost(最小费用最大流 spfa算法求最短路)

题意：有N个店主，M个供应商，K种物品。每个供应商对每种物品的的供应量已知，每个店主对每种物品的需求量的已知，从不同的供应商运送不同的货物到不同的店主手上需要不同的花费，又已知从供应商Mj送第kind种货物的单位数量到店主Ni手上所需的单位花费。

问：供应是否满足需求？如果满足，最小运费是多少？

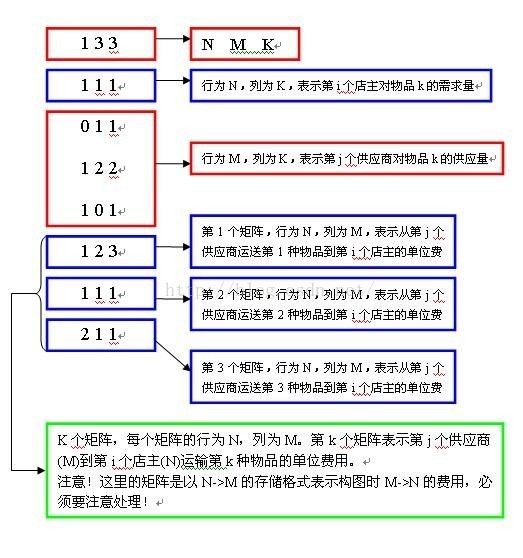
对于输入格式：

思路：最小费用最大流。先判断是否每种货物的存储总量都足够，足够的话，对每一种货物进行一次最小费用最大流求出完成这种货物运输的最小总费用，所有的总费用相加就是结果了。

参考资料：

http://www.360doc.com/content/13/1208/22/14357424_335569176.shtml

http://blog.sina.com.cn/s/blog_6635898a0100pabw.html

#include<iostream>
#include<string.h>
#include<stdio.h>
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
const int Max = 110;
const int inf = 99999999;

int n, ans;
int cap[Max][Max], pre[Max];//流量
int cost[Max][Max], dis[Max];//单位费用
int que[Max];
bool vis[Max];

bool spfa(){
    int i, head = 0, tail = 1;
    for(i = 0; i <= n; i ++){
        dis[i] = inf;
        vis[i] = false;
    }
    dis[0] = 0;
    que[0] = 0;
    while(tail != head){
        int u = que[head];
        vis[u] = true;
        for(i = 0; i <= n; i ++)
            if(cap[u][i] && dis[i] > dis[u] + cost[u][i]){
                dis[i] = dis[u] + cost[u][i];
                pre[i] = u;
                if(!vis[i]){
                    vis[i] = true;
                    que[tail ++] = i;
                    if(tail == Max) tail = 0;
                }
            }
        vis[u] = false;
        head ++;
        if(head == Max) head = 0;
    }
    if(dis[n] == inf) return false;
    return true;
}

void end(){
    int i, sum = inf;
    for(i = n; i != 0; i = pre[i])
        sum = min(sum, cap[pre[i]][i]);
    for(i = n; i != 0; i = pre[i]){
        cap[pre[i]][i] -= sum;
        cap[i][pre[i]] += sum;
        ans += cost[pre[i]][i] * sum;
    }
}

int main(){
    int N, M, K, i, j, k;
    int need[Max][Max], NeedK[Max];
    int have[Max][Max], HaveK[Max];
    while(scanf("%d%d%d", &N, &M, &K) && N){
        memset(NeedK, 0, sizeof(NeedK));
        for(i = 1; i <= N; i ++)
            for(j = 1; j <= K; j ++){
                scanf("%d", &need[i][j]);    //  第i个客户需要第j种货物的量。
                NeedK[j] += need[i][j];      //  第j种货物总共需要的量。
            }
        memset(HaveK, 0, sizeof(HaveK));
        for(i = 1; i <= M; i ++)
            for(j = 1; j <= K; j ++){
                scanf("%d", &have[i][j]);    //  第i个仓库存储第j种货物的量。
                HaveK[j] += have[i][j];      //  第j种货物总共需要的量。
            }
        bool flag = true;
        for(i = 1; i <= K; i ++)             //  判断所有货物是否足够。
            if(NeedK[i] > HaveK[i]){
                flag = false; break;
            }
        ans = 0;
        n = N + M + 1;
        for(k = 1; k <= K; k ++){
            memset(cap, 0, sizeof(cap));
            for(i = 1; i <= N; i ++)         //  建图。
                for(j = 1; j <= M; j ++){
                    scanf("%d", &cost[j][M+i]);
                    cost[M+i][j] = -cost[j][M+i];
                    cap[j][M+i] = inf;
                }
            if(!flag) continue;
            for(i = 1; i <= M; i ++){
                cap[0][i] = have[i][k];
                cost[0][i] = cost[i][0] = 0;
            }
            for(i = 1; i <= N; i ++){
                cap[M+i][n] = need[i][k];
                cost[M+i][n] = cost[n][M+i] = 0;
            }
            while(spfa()) end();            //  最小费用最大流算法。
        }
        if(flag) cout << ans << endl;
        else cout << -1 << endl;
    }
    return 0;
}