hdu1828 Picture
Problem Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
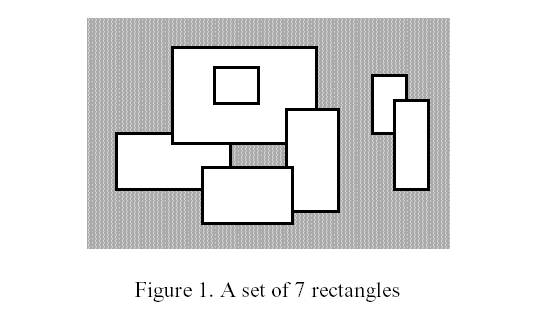
The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
这道题和求矩形面积差不多,但难度更大,现在只会第一种方法,有时间再学第二种。这里我用两次扫描,扫描x轴和y轴,每家入一条线段,如果投影在x轴或者y轴上的总长度发生改变,那么就加上这条线段的长度。
<pre name="code" class="cpp">#include<stdio.h> #include<string.h> #include<math.h> #include<algorithm> using namespace std; struct edge{ int x2,x3,y,f; }s[5005*2]; struct edge1{ int y2,y3,x,f; }s1[5005*2]; int sum[5005*2],sum1[5005*2]; bool cmp1(edge a,edge b){ return a.y<b.y; } bool cmp2(edge1 a,edge1 b){ return a.x<b.x; } struct node{ int l,r,cnt,len; }b[2*10100*4]; void build(int l,int r,int i) { int mid; b[i].l=l;b[i].r=r;b[i].cnt=b[i].len=0; mid=(l+r)>>1; if(l==r)return; build(l,mid,i<<1); build(mid+1,r,i<<1|1); } void getline(int i) { if(b[i].cnt)b[i].len=b[i].r-b[i].l+1; else if(b[i].l==b[i].r)b[i].len=0; else b[i].len=b[i<<1].len+b[i<<1|1].len; } void update(int l,int r,int add,int i) { int mid; if(b[i].l==l && b[i].r==r){ b[i].cnt+=add; getline(i);return; } mid=(b[i].l+b[i].r)>>1; if(r<=mid)update(l,r,add,i<<1); else if(l>mid)update(l,r,add,i<<1|1); else{ update(l,mid,add,i<<1); update(mid+1,r,add,i<<1|1); } getline(i); } int main() { int n,m,i,j,x2,x3,y2,y3,num,ans,num1; while(scanf("%d",&n)!=EOF) { if(n==0){ printf("0\n");continue; } num=0;num1=0; for(i=1;i<=n;i++){ scanf("%d%d%d%d",&x2,&y2,&x3,&y3); num++; s[num].x2=x2;s[num].x3=x3;s[num].y=y2;s[num].f=1; num++; s[num].x2=x2;s[num].x3=x3;s[num].y=y3;s[num].f=-1; num1++; s1[num1].y2=y2;s1[num1].y3=y3;s1[num1].x=x2;s1[num1].f=1; num1++; s1[num1].y2=y2;s1[num1].y3=y3;s1[num1].x=x3;s1[num1].f=-1; } sort(s+1,s+1+num,cmp1); build(-10000,10000,1); memset(sum,0,sizeof(sum)); sum[0]=0;ans=0; for(i=1;i<=num;i++){ update(s[i].x2,s[i].x3-1,s[i].f,1); sum[i]=b[1].len; if(abs(sum[i]-sum[i-1])>0)ans+=abs(sum[i]-sum[i-1]); } sort(s1+1,s1+1+num1,cmp2); build(-10000,10000,1); memset(sum1,0,sizeof(sum1)); sum1[0]=0; for(i=1;i<=num1;i++){ update(s1[i].y2,s1[i].y3-1,s1[i].f,1); sum1[i]=b[1].len; if(abs(sum1[i]-sum1[i-1])>0)ans+=abs(sum1[i]-sum1[i-1]); //printf("%d\n",ans); } printf("%d\n",ans); } return 0; }