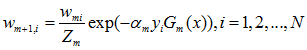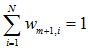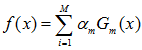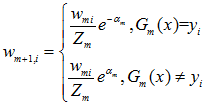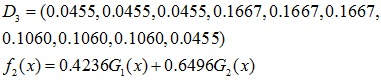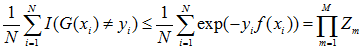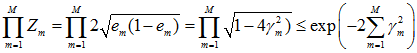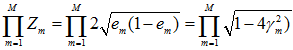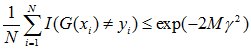提升方法(boosting)详解
注:本文非笔者原创,原文转载自:http://www.sigvc.org/bbs/thread-727-1-1.html
提升方法是基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。通俗点说,就是”三个臭皮匠顶个诸葛亮”。
Leslie Valiant首先提出了“强可学习(strongly learnable)”和”弱可学习(weakly learnable)”的概念,并且指出:在概率近似正确(probably approximately correct, PAC)学习的框架中,一个概念(一个类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的,如果正确率不高,仅仅比随即猜测略好,那么就称这个概念是弱可学习的。
2010年的图灵奖给了L. Valiant,以表彰他的PAC理论。非常有趣的是Schapire后来证明强可学习与弱可学习是等价的,也就是说,在PAC学习的框架下,一个概念是强可学习的充要条件是这个概念是可学习的。
这样一来,问题便成为,在学习中,如果已经发现了“弱学习算法”,那么能否将它提升(boost)为”强学习算法”。大家知道,发现弱学习算法通常比发现强学习算法容易得多。那么如何具体实施提升,便成为开发提升方法时所要解决的问题。关于提升方法的研究很多,有很多算法被提出。最具代表性的是AdaBoost算法(Adaptive Boosting Algorithm),可以说,AdaBoost实现了PAC的理想。
对于分类问题而言,给定一个训练数据,求一个比较粗糙的分类器(即弱分类器)要比求一个精确的分类器(即强分类器)容易得多。提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器,然后组合这些弱分类器,构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布(训练数据中的各个数据点的权值分布),调用弱学习算法得到一个弱分类器,再改变训练数据的概率分布,再调用弱学习算法得到一个弱分类器,如此反复,得到一系列弱分类器。
这样,对于提升方法来说,有两个问题需要回答:一是在每一轮如何如何改变训练数据的概率分布;而是如何将多个弱分类器组合成一个强分类器。
关于第一个问题,AdaBoost的做法是,提高那些被前几轮弱分类器线性组成的分类器错误分类的的样本的权值。这样一来,那些没有得到正确分类的数据,由于权值加大而受到后一轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器”分而治之”。至于第二个问题,AdaBoost采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
AdaBoost的巧妙之处就在于它将这些想法自然而然且有效地实现在一种算法里。
输入:训练数据集T={(x1,y1),(x2,y2),…,(xN,yN)},其中xi∈X⊆Rn,表示输入数据,yi∈Y={-1,+1},表示类别标签;弱学习算法。
输出:最终分类器G(x)。
流程:
- 初始化训练数据的概率分布,刚开始为均匀分布
D1=(w11,w12,…,w1N), 其中w1i=
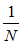 , i=1,2,..,N
, i=1,2,..,N
- 对m=1,2,…,M,
- 使用具有权值分布Dm的训练数据集进行学习(任意选一种模型都可以,例如朴素贝叶斯,决策树,SVM等,并且每一轮迭代都可以用不同的模型),得到一个弱分类器
- 计算Gm(x)在训练数据集上的分类误差率
- 计算弱分类器Gm(x)的系数
- 更新训练数据的权值分布
这里,Zm是规范化因子
- 将M个基本分类器进行线性组合
得到最终分类器
对AdaBoost算法作如下说明:
步骤(1) 初始时假设训练数据集具有均匀分布,即每个训练样本在弱分类器的学习中作用相同。
步骤(2) (c) αm表示Gm(x)在最终分类器中的重要性。由式(公式 2)可知,当em ≤1/2时,αm≥0,并且αm随着em的减小而增大,即意味着误差率越小的基本分类器在最终分类器中的作用越大。
(d) 式(公式 4)可以写成:
由此可知,被弱分类器Gm(x)误分类的样本的权值得以扩大,而被正确分类的样本的权值得以缩小。因此误分类样本在下一轮学习中起到更大的作用。不改变所给的训练数据,而不断改变训练数据权值的分布,使得训练数据在基本分类器的学习中起不同的作用,这是AdaBoost的一个特点。
步骤(3) 这里,αm之和并不等于1。f(x)的符号决定实例x的类别,f(x)的绝对值表示分类的确信度。利用基本分类器进行线性组合得到最终分类器是AdaBoost的另一个特点。
例 1 给定如表 1所示训练数据。假设弱分类器由G(x)=sign(x-v)产生,其中v为常量,表示阀值。试用AdaBoost算法学习一个强分类器。
表 1 训练数据样本
解
初始化训练数据的权值分布
当m=1,进行第一轮迭代
- 在权值分布为D1的情况下,用一根垂直扫描线从左到右扫描,会发现,阀值v取2.5时分类误差率最低,故基本分类器G1(x)=sign(x-2.5)。
- G1(x)在训练数据集上的误差率

,第7,8,9个实例被误分类。
- 计算G1(x)的系数:
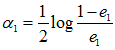 =0.4236。
=0.4236。
- 更新训练数据的权值分布:
分类器sign[f1(x)]在训练数据集上有3个误分类点,因此,继续迭代。
当m=2,进行第二轮迭代
- 在权值分布为D2的情况下,阀值v取8.5时分类误差率最低,故基本分类器G2(x)=sign(x-8.5)。
- G2(x)在训练数据集上的误差率e2=0.07143+0.07143+0.07143+0.07143,第4,5,6个实例被错误分类。
- 计算G2(x)的系数:α2=0.6496。
- 更新训练数据的权值分布:
分类器sign[f2(x)]在训练数据集上有3个误分类点,因此,继续迭代。
当m=3,进行第三轮迭代
- 在权值分布为D3的情况下,阀值v取5.5时分类误差率最低,故基本分类器G3(x)=-sign(x-5.5),注意,这里符号反向了。
- G3(x)在训练数据集上的误差率e3=0.0455+0.0455+0.0455+0.0455=0.1820,第1,2,3,10个实例被误分类。
- 计算G3(x)的系数:α2=0.7514。
- 更新训练数据的权值分布:
分类器sign[f3(x)]在训练数据集上的误分类点个数为0,因此,终止迭代。
于是,最终分类器为
注意,G1(x),G2(x)和G3(x),是一个sign函数,从图像看是一个方波图,而最终分类器G(x)也是一个方波图,由三个波形图叠加合成。从信号的角度看,这是振幅叠加。G1(x),G2(x)和G3(x)都是弱分类器,分类正确率仅大于0.5,但线性组合而成的分类器G(x)正确率是100%,是一个强分类器。
AdaBoost算法的训练误差分析
AdaBoost最基本的性质是它能在学习过程中不断减少训练误差,关于这个问题有下面的两个定理:
定理 1 (AdaBoost的训练误差界) AdaBoost算法的最终分类器的训练误差界为
这里,G(x),f(x)和Zm分别由(公式 7)、(公式 6)和(公式 5)给出。
证明
当G(xi) ≠yi时,I(G(xi) ≠yi)=1,yif(xi) < 0,因而exp(-yif(xi)) ≥1,所以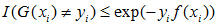 成立;
成立;
当G(xi) ≠yi时,I(G(xi) ≠yi)=1,yif(xi) < 0,因而exp(-yif(xi)) ≥1,所以
当G(xi) =yi时,I(G(xi) ≠yi)=0,又因为exp(-yif(xi)) ≥0,所以
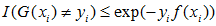 成立;
成立;
可见,
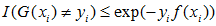 恒成立。
恒成立。
不等式的后半部分推导要用到Zm的定义式(公式 5)及(公式 4)的变形:
先推导如下:
(
定理 1的证明@特级飞行员舒克有很大贡献)
这一定理说明,可以在每一轮选取最适当的Gm使得Zm最小,从而使训练误差下降最快。对二类分类问题,有如下结果:
定理 2 (二类分类问题AdaBoost的训练误差界)
证明
由Zm的定义式(公式 5)得
由Zm的定义式(公式 5)得
推论 1
如果存在γ>0,对所有m有γm≥γ,则
如果存在γ>0,对所有m有γm≥γ,则
这表明在此条件下,AdaBoost的训练误差是以指数速率下降的。这一性质当然是很有吸引力的。
注意,AdaBoost算法不需要知道下界γ。这正是Freund与Schapire设计AdaBoost时所考虑的。与一些早期的提升方法不同,AdaBoost具有适应性,即它能适应弱分类器各自的训练误差率。这也是它的名称的由来,Ada是Adaptive的简写。