几何方法---测试盒子
测试一个盒子是比球体和点更棘手的问题。一个简单的方式就是测试盒子的八个点。一个简单的方法认为就是如果所有的点都是在视景体之外那么可以认为在视景体之外。
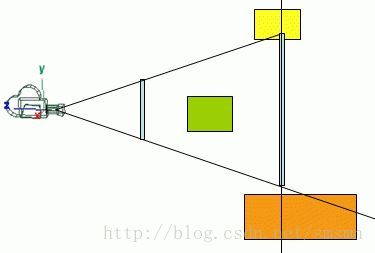
然而下面的图展示了这个并不总是这个情况。
黄色盒子的点都在视景体之外,但是盒子有部分在视景体之内,因此它不应该被抛弃。一个安全的方式来解决这个问题来抛弃这个盒子,也仅仅,所有的点在同一个平面的错误边。在上面的黄色盒子中并没有这样的平面。
这里有不是太好的方式来解决这个方案:在下图中,橘红色的球体,虽然总的通过这个测试的是在视景体之外。两个选项是有效的,接收这些盒子因为测试的代价应该保持到最低,或者做一些更远的测试。
在这里第一种方案被采取,因此有些在视景体之外的也会接收,为了将代价降到最低(Assarsson and Moller可以寻找一些通过长远测试的方式)。
int FrustumG::boxInFrustum(Box &b) {
int result = INSIDE, out,in;
// for each plane do ...
for(int i=0; i < 6; i++) {
// reset counters for corners in and out
out=0;in=0;
// for each corner of the box do ...
// get out of the cycle as soon as a box as corners
// both inside and out of the frustum
for (int k = 0; k < 8 && (in==0 || out==0); k++) {
// is the corner outside or inside
if (pl[i].distance(b.getVertex(k)) < 0)
out++;
else
in++;
}
//if all corners are out
if (!in)
return (OUTSIDE);
// if some corners are out and others are in
else if (out)
result = INTERSECT;
}
return(result);
}
这个函数对于每个平面的更复杂的方式,球体的八个点都有可能被测试。注意有两个新的变量in和out被声明定义。这些变量跟踪,对于每个平面在两边的顶点个数。如果所有的点都是在边的错误边那么in将变为0,然后盒子将会直接被丢弃,如果顶点在平面的两边,那么这个盒子会跟视景体相交的。如果一个盒子的所有点在所有平面的非错误边那么是在视景体之内,那么它将不会跟任何平面有交点。
如果有点在平面的两边,那么还要做一次点的测试(注意,通知停止条件周期)。意味着跟平面有相交。
英文地址
博客地址:http://www.arcosu.com/post/index/102