Mahout fp-growth
FP-growth
Apriori算法的一个主要瓶颈在于,为了获得较长的频繁模式,需要生成大量的候选短频繁模式。FP-Growth算法是针对这个瓶颈提出来的全新的一种算法模式。目前,在数据挖掘领域,Apriori和FP-Growth算法的引用次数均位列三甲。参看论文《Mining Frequence PatternsWithout Candidate Generation》 。
FP的全称是Frequent Pattern,在算法中使用了一种称为频繁模式树(Frequent Pattern Tree)的数据结构。FP-tree是一种特殊的前缀树,由频繁项头表和项前缀树构成。所谓前缀树,是一种存储候选项集的数据结构,树的分支用项名标识,树的节点存储后缀项,路径表示项集。
一、算法流程
频繁集的阈值是3,最小支持度为3。
事务数据:
图(1)
首先,扫一遍数据,统计每一项的频率;删除频率小于最小支持度的项;根据项频率,由大到小排序。
然后再扫一遍数据,构造频繁项集树。构造树的流程如下。
读第一条记录:
图(2)
读第二条记录:
图(3)
读第三条记录:
图(4)
读第四条记录:
图(5)
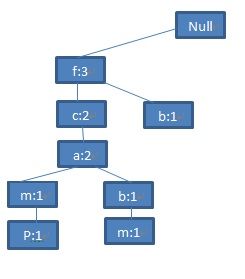
读第五条记录:
图(6)
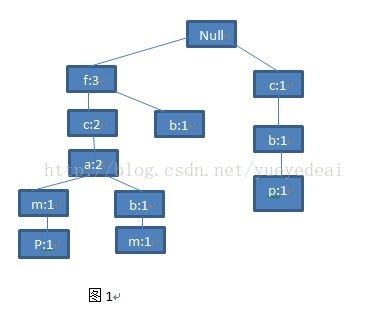
为了便于后边的树的遍历,我们为这棵树又增加了一个结构-头表,头表保存了所有的频繁项目,并且按照频率的降序排列,表中的每个项目包含一个节点链表,指向树中和它同名的节点。
图(7)
好了,一颗完整的FP-Tree构造完成。
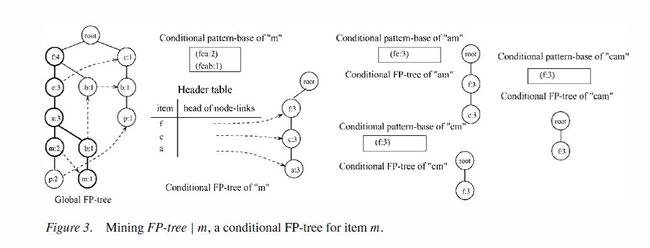
二、挖掘频繁模式
图(8)
以m为例挖掘,以m结尾的有{f:4,c:3,a:3,m:2}和{f:4,c:3,a:3,b:1,m:1}两条路径。以m为条件,{f:4,c:3,a:3,m:2}得到{fca:2},{f:4,c:3,a:3,b:1,m:1}得到{fcab:1}。两项相加得到{fca:3,b:1},b不符合频繁项阈值3,所以,
mine(FPtree|m)=mine(<f:3,c:3,a:3>|m)。
其他以此类推,得到最终的结果,如下图。
图(9)
三、MapReduce实现
(一)流程图
Step1:item计数
Map:
| f:1 ,a:1 ,c;1,d:1,g:1,i:1,m:1,p:1 |
| a:1,b:1,c:1,f:1,l:1,m:1,o:1 |
| b:1,f;1 ,h;1,j;1,o:1 |
| b:1,c:1,k:1,s:1,p:1 |
| a:1,f;1,c:1,e:1,l:1,p:1,m:1,n:1 |
Reduce:
| f:4 |
| c:4 |
| a:3 |
| m:3 |
| P:3 |
Step2:删除最小支持度的item,特征排序
| f,c,a,m,p |
| f,c,a,b,m |
| f,b |
| c,b,p |
| f,c,a,m,p |
Step3:分组
| 1
|
f |
| c |
|
| 2 |
a |
| b |
|
| 3 |
m |
| p |
Step4:
Map:
| f,c |
{f, <c,a,m,p>:1} , {f,<c,a,b,m>:1} |
| a.b |
{f,<b>:1}, {c, <b,p>:1} |
| m,p |
{f,<c,a,m,p>:1} |
Reduce:
| f,{<c,a,m,p>:1, <c,a,b,m>:1, <b>:1, <c,a,m,p>:1} |
| c,{<b,p>:1} |
Step5:
Map:
| f,<c,a,m,p>:1 |
{p,<c,a,m,p>:1},{m,<c,a>:1},{a,<c,a>:1},{c,<c>:1} |
| f,<c,a,b,m>:1 |
{m,<c,a,b,m>:1},{b,<c,a,b>:1},{a,<c,a>:1},{c,<c>:1} |
| f,<b>:1 |
{b,<b>:1} |
| f,<c,a,m,p>:1 |
{p,<c,a,m,p>:1},{m,<c,a,m>:1},{a,<c,a>:1},{c,<c>:1} |
| c,<b,p>:1 |
{p,<b,p>:1},{b,<b>:1} |
Reduce:
| f,c |
{c,<c>:3} |
| a,b |
{a,<c,a>:3},{b,<c:1,a:1,b:3>} |
| m,p |
{m,<c:3,a:3,b:1,m:3>},{p,<c;3,b:1,a:2,m:2,p:3>} |
Step6:
|
(二)startParallelCounting();
输入的是文本数据,key为行号,value为文本中的一行,分割。
第一遍扫数据集。Map中分割一行,然后计数,在reduce中求和。类似于WordCount实例。
(三)startGroupingItems();
(1)读取上一步的结果,删除Item数量<最小支持度的Item。
(2)将Item分组,默认分为50组。
(四)startTransactionSorting();
第二遍扫数据集。
Map:分割一行数据,如果没有在特征集中的项,跳过。根据之前统计出的Item 特征的数量大小排序分割后的Item(由大到小排序),组成 a[]。
输出格式为:key a[0],value <a[a.length] ,1> 。1表示支持度为1。
Reduce: 排序号的相同前缀的项集(即a[0]相同),汇聚到同一个Reduce中。
输出格式为:1,<a[a.length] ,1>
(五)startParallelFPGrowth();
输入前一个Job的输出。
Map:
setUp(){
从配置信息中获取Item的分组信息。
}
对<a[a.length] ,1>,计算子模式。
比如如对 ({a,b,c,d,e} ,1) ,输出为:
<groupId(e),({a,b,c,d,e},1)>,
<groupId(d),({a,b,c,d},1)>,
<groupId(c),({a,b,c},1)>,
<groupId(b),({a,b},1)>,
<groupId(a),({a},1)>
Combier:
对相同组的key合并,构建一个子树。
输出为合并后的子树。
Reduce:
1.对相同组的key,做全局合并,构建一个子树。原理为树的合并算法。
2.对该组数据,构建Head-table,项排序顺序为它的数量由大到小。
3.对该组数据中的每一个Head-table特征,挖掘Top k个频繁模式,原理如图(8)。
4.输出:Text key,TopKStringPatterns values 。Key为特征编号,value为该特征的Top k个频繁模式。
输出数据为:m,<{f,c,a},2>}和{m,<{f,c,a,b},1>}
(六)startAggregating();
Map:
输入数据为 {m,<{f,c,a},2>}和{m,<{f,c,a,b},1>}。
对数据{m,<{f,c,a},2>},输出为{mf,<{f,c,a},2>}、{mc,<{f,c,a},2>}和{ma,<{f,c,a},2>}。
对数据{m,<{f,c,a,b},1>},输出为{mf,<{f,c,a,b},1>}、{mc,<{f,c,a,b},1>}、 {ma,<{f,c,a,b},1>}、{mb,<{f,c,a,b},1>}
Reduce:
Map中相同key的频繁模式合并。
对上面数据,合并为{mf,<f:3,c:3,a:3,b:1>}或{mc,<f:3,c:3,a:3,b:1>}或{ma,<f:3,c:3,a:3,b:1>}或{mb,<f:1,c:1,a:1,b:1>}
过滤掉不满足阈值的项。结果为{m,<{f,c,a},3>}
四、API说明
API
| FPGrowthDriver.main(arg); |
|
| --minSupport (-s) |
最小支持度 |
| --input (-i) input |
输入路径 |
| -output (-o) |
输出路径 |
| --maxHeapSize (-k) (Optional) |
挖掘最少k个item |
| --numGroups (-g) |
特征分组数 |
| --method (-method) |
Sequential或mapreduce |
| --encoding (-e) |
默认UTF-8 |
| --numTreeCacheEntries (-tc) |
缓存大小,默认5 |
| --splitterPattern (-regex) |
默认"[ ,\t]*[,|\t][ ,\t]*" |
输入文件示例(文本文件)
| f,g,d,e,b,c,a,j,k,h,i f,g,d,e,c,j,k,h,i f,d g,b,j,i g,e,a,k f,g,d,e,b,c,a,k,h,i f,g,d,b,c,j,k f,g,d,e,b,c,a,j,k,h,i f,b,j f,g,e,b,c,a,j,k,h,i f,g,b,c,k,h,i g,e,c,a,j,k,h,i f,g,e,c,k,i d |
示例
| String [] arg ={"-s","5", "-i","fp/data.txt", "-o","fpgrowth" ,"-k","4", "-g","50", "-method","mapreduce", "-e","UTF-8", "-tc","5"}; FPGrowthDriver.main(arg); |
输出格式
| 结果文件 |
Key类型 |
Value类型 |
| frequentpatterns |
Item (org.apache.hadoop.io.Text) |
模式(org.apache.mahout.fpm.pfpgrowth.convertors.string.TopKStringPatterns) |
输出文件转成文本结果
| Key: a: Value: ([a],122), ([d, a],89), ([b, a],87), ([b, d, a],67) Key: b: Value: ([b],129), ([g, b],92), ([k, b],91), ([b, d],90) Key: c: Value: ([c],121), ([k, c],88), ([g, c],88), ([k, g, c],69) Key: d: Value: ([d],128), ([g, d],90), ([b, d],90), ([d, a],89) Key: e: Value: ([e],121), ([k, e],87), ([g, e],86), ([k, g, e],63) Key: f: Value: ([f],120), ([g, f],91), ([b, f],89), ([g, b, f],71) Key: g: Value: ([g],130), ([k, g],94), ([g, b],92), ([g, f],91) Key: h: Value: ([h],110), ([g, h],81), ([k, h],80), ([k, g, h],61) Key: i: Value: ([i],119), ([k, i],88), ([g, i],84), ([k, g, i],68) Key: j: Value: ([j],121), ([g, j],90), ([k, j],88), ([k, g, j],68) Key: k: Value: ([k],133), ([k, g],94), ([k, b],91), ([k, j],88) |
五、参考文献
1.《MiningFrequent Patterns without Candidate Generation》JiaweiHan, Jian Pei, and Yiwen Yin
2.《FP-Growth 算法MapReduce 化研究》 吕雪骥,李龙澍
3.博客:http://blog.sina.com.cn/s/blog_6fb7db430100vdj7.html