几何方法---扩展的平面
这个几何方法操作是在世界空间中,并且使用了视景体的形状用来定义包围的视景体的扩展六个平面的信息:近平面,远平面,顶平面,底平面,左平面和右平面。
平面是用像法向量朝向视景体内部的定义。测试如果一个物体是在视景体内部就是计算物体的是在平面的哪一边。这个可以通过计算从点到平面的距离。如果它是在一个法向量点的一边,比如说,计算的点是负的,那么它就是在各自平面的右边,如果一个物体都是在所有六个平面那么物体是在视景体内部。
在这一节中我们将提供计算六个视景体平面的方法。测试将在下一节介绍。
一个靠近的方法,视景体角的八个顶点,然后使用这些点来定义这些平面。
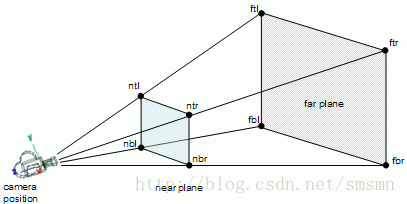
下图就是用来展示这些点用来定义六个平面:
用来定义这些点的符号如下:第一个字母代表是点是在近平面(n)或者远平面(f);第二个字母代表的是点是在顶点(t)或者底端(b);第三个字母代表的是左边(l)或者右边(r)。
让我们在回顾一下前面一节介绍的信息:
1. p-相机的位置;
2. d-相机的视线方向向量。在这里我们假定向量已经归一化。
3. nearDist-相机到近平面的距离。
4. farDist-相机到远平面的距离。
5. Hnear-近平面的高度。
6. Wnear-近平面的宽度
7. Hfar-远平面的高度
8. Wfar-远平面的宽度
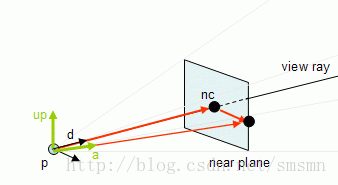
还有更多的向量需要,就是叫做up 向量和 right向量。前者包含向量(ux, uy, uz)(这个向量的成分是在函数gluLookAt的最后三个参数);后面那个是包含up向量和d向量的叉乘结果。
下图包含了远平面的左顶端的部分,就是ftl。
为了计算ftl需要下面的向量数学计算:
fc = p + d * farDist;
ftl = fc + (up * Hfar / 2) - (right * Wfar / 2)
剩下部分的计算如下:
ftr = fc + (up * Hfar/2) + (right * Wfar/2)
fbl = fc - (up * Hfar/2) - (right * Wfar/2)
fbr = fc - (up * Hfar/2) + (right * Wfar/2)
nc = p + d * nearDist
ntl = nc + (up * Hnear/2) - (right * Wnear/2)
ntr = nc + (up * Hnear/2) + (right * Wnear/2)
nbl = nc - (up * Hnear/2) - (right * Wnear/2)
nbr = nc - (up * Hnear/2) + (right * Wnear/2)
一个平面可以用三个点来定义。实际上,为了定义远平面可以使用以下点:ftl, ftr, 和fbr。我们应该确保法线朝向适当的方向,实际上所有的方向应该朝向视景体的里面,请看数学库中的平面。
一个优化的方法用来计算近平面和远平面。一个平面可以用一个法线和顶点来定义,这些平面都可以用相机的定义来知道。
近平面可以用d来定义法向量,和nc是平面中的一个点。因此远平面的法线是-d和点是fc。
其他平面同样可以拥有更有效的方式来计算,也就是使用一个法向量和一个点来定义一个平面。下面的代码用来右平面的法向量。因为点,相机的位置,p是在所有顶、底、左边和右边面的点(包括一个透视投影)。
nc = p + d * nearDist
fc = p + d * farDist
a = (nc + right * Wnear / 2) - p
a.normalize();
normalRight = up * a
所有的up和a向量是属于右边平面,因此它们的叉乘提供一个平面的法向量。
英文地址
我的博客地址:http://www.arcosu.com/post/index/99