拓扑排序的原理及其实现

本文将从以下几个方面介绍拓扑排序：

• 拓扑排序的定义和前置条件
• 和离散数学中偏序/全序概念的联系
• 典型实现算法
  • Kahn算法
  • 基于DFS的算法

• 解的唯一性问题
• 实际例子

取材自以下材料：

http://en.wikipedia.org/wiki/Topological_sorting

http://en.wikipedia.org/wiki/Hamiltonian_path

定义和前置条件：

定义：将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。

 

如果这个概念还略显抽象的话，那么不妨考虑一个非常非常经典的例子——选课。我想任何看过数据结构相关书籍的同学都知道它吧。假设我非常想学习一门机器学习的课程，但是在修这么课程之前，我们必须要学习一些基础课程，比如计算机科学概论，C语言程序设计，数据结构，算法等等。那么这个制定选修课程顺序的过程，实际上就是一个拓扑排序的过程，每门课程相当于有向图中的一个顶点，而连接顶点之间的有向边就是课程学习的先后关系。只不过这个过程不是那么复杂，从而很自然的在我们的大脑中完成了。将这个过程以算法的形式描述出来的结果，就是拓扑排序。

 

那么是不是所有的有向图都能够被拓扑排序呢？显然不是。继续考虑上面的例子，如果告诉你在选修计算机科学概论这门课之前需要你先学习机器学习，你是不是会被弄糊涂？在这种情况下，就无法进行拓扑排序，因为它中间存在互相依赖的关系，从而无法确定谁先谁后。在有向图中，这种情况被描述为存在环路。因此，一个有向图能被拓扑排序的充要条件就是它是一个有向无环图(DAG：Directed Acyclic Graph)。

偏序/全序关系：

偏序和全序实际上是离散数学中的概念。

这里不打算说太多形式化的定义，形式化的定义教科书上或者上面给的链接中就说的很详细。

 

还是以上面选课的例子来描述这两个概念。假设我们在学习完了算法这门课后，可以选修机器学习或者计算机图形学。这个或者表示，学习机器学习和计算机图形学这两门课之间没有特定的先后顺序。因此，在我们所有可以选择的课程中，任意两门课程之间的关系要么是确定的(即拥有先后关系)，要么是不确定的(即没有先后关系)，绝对不存在互相矛盾的关系(即环路)。以上就是偏序的意义，抽象而言，有向图中两个顶点之间不存在环路，至于连通与否，是无所谓的。所以，有向无环图必然是满足偏序关系的。

 

理解了偏序的概念，那么全序就好办了。所谓全序，就是在偏序的基础之上，有向无环图中的任意一对顶点还需要有明确的关系(反映在图中，就是单向连通的关系，注意不能双向连通，那就成环了)。可见，全序就是偏序的一种特殊情况。回到我们的选课例子中，如果机器学习需要在学习了计算机图形学之后才能学习(可能学的是图形学领域相关的机器学习算法……)，那么它们之间也就存在了确定的先后顺序，原本的偏序关系就变成了全序关系。

 

实际上，很多地方都存在偏序和全序的概念。

比如对若干互不相等的整数进行排序，最后总是能够得到唯一的排序结果(从小到大，下同)。这个结论应该不会有人表示疑问吧:)但是如果我们以偏序/全序的角度来考虑一下这个再自然不过的问题，可能就会有别的体会了。

 

那么如何用偏序/全序来解释排序结果的唯一性呢？

我们知道不同整数之间的大小关系是确定的，即1总是小于4的，不会有人说1大于或者等于4吧。这就是说，这个序列是满足全序关系的。而对于拥有全序关系的结构(如拥有不同整数的数组)，在其线性化(排序)之后的结果必然是唯一的。对于排序的算法，我们评价指标之一是看该排序算法是否稳定，即值相同的元素的排序结果是否和出现的顺序一致。比如，我们说快速排序是不稳定的，这是因为最后的快排结果中相同元素的出现顺序和排序前不一致了。如果用偏序的概念可以这样解释这一现象：相同值的元素之间的关系是无法确定的。因此它们在最终的结果中的出现顺序可以是任意的。而对于诸如插入排序这种稳定性排序，它们对于值相同的元素，还有一个潜在的比较方式，即比较它们的出现顺序，出现靠前的元素大于出现后出现的元素。因此通过这一潜在的比较，将偏序关系转换为了全序关系，从而保证了结果的唯一性。

 

拓展到拓扑排序中，结果具有唯一性的条件也是其所有顶点之间都具有全序关系。如果没有这一层全序关系，那么拓扑排序的结果也就不是唯一的了。在后面会谈到，如果拓扑排序的结果唯一，那么该拓扑排序的结果同时也代表了一条哈密顿路径。

典型实现算法：

Kahn算法：

摘一段维基百科上关于Kahn算法的伪码描述：

L← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
    remove a node n from S
    insert n into L
    foreach node m with an edge e from nto m do
        remove edge e from thegraph
        ifm has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least onecycle)
else 
    return L (a topologically sortedorder)

 

不难看出该算法的实现十分直观，关键在于需要维护一个入度为0的顶点的集合：

每次从该集合中取出(没有特殊的取出规则，随机取出也行，使用队列/栈也行，下同)一个顶点，将该顶点放入保存结果的List中。

紧接着循环遍历由该顶点引出的所有边，从图中移除这条边，同时获取该边的另外一个顶点，如果该顶点的入度在减去本条边之后为0，那么也将这个顶点放到入度为0的集合中。然后继续从集合中取出一个顶点…………

 

当集合为空之后，检查图中是否还存在任何边，如果存在的话，说明图中至少存在一条环路。不存在的话则返回结果List，此List中的顺序就是对图进行拓扑排序的结果。

实现代码：

 public class KahnTopological
 {
     private List<Integer> result;   // 用来存储结果集
     private Queue<Integer> setOfZeroIndegree;  // 用来存储入度为0的顶点
     private int[] indegrees;  // 记录每个顶点当前的入度
     private int edges;
     private Digraph di;

     public KahnTopological(Digraph di)
     {
         this.di = di;
         this.edges = di.getE();
         this.indegrees = new int[di.getV()];
         this.result = new ArrayList<Integer>();
         this.setOfZeroIndegree = new LinkedList<Integer>();

         // 对入度为0的集合进行初始化
         Iterable<Integer>[] adjs = di.getAdj();
         for(int i = 0; i < adjs.length; i++)
         {
             // 对每一条边 v -> w
             for(int w : adjs[i])
             {
                 indegrees[w]++;
             }
         }

         for(int i = 0; i < indegrees.length; i++)
         {
             if(0 == indegrees[i])
             {
                 setOfZeroIndegree.enqueue(i);
             }
         }
         process();
     }

     private void process()
     {
         while(!setOfZeroIndegree.isEmpty())
         {
             int v = setOfZeroIndegree.dequeue();

             // 将当前顶点添加到结果集中
             result.add(v);

             // 遍历由v引出的所有边
             for(int w : di.adj(v))
             {
                 // 将该边从图中移除，通过减少边的数量来表示
                 edges--;
                 if(0 == --indegrees[w])   // 如果入度为0，那么加入入度为0的集合
                 {
                     setOfZeroIndegree.enqueue(w);
                 }
             }
         }
         // 如果此时图中还存在边，那么说明图中含有环路
         if(0 != edges)
         {
             throw new IllegalArgumentException("Has Cycle !");
         }
     }

     public Iterable<Integer> getResult()
     {
         return result;
     }
 }

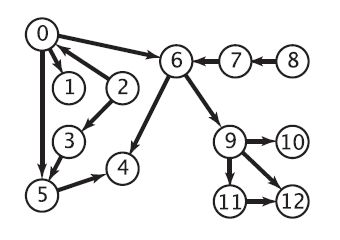
对上图进行拓扑排序的结果：

2->8->0->3->7->1->5->6->9->4->11->10->12

复杂度分析：

初始化入度为0的集合需要遍历整张图，检查每个节点和每条边，因此复杂度为O(E+V);

然后对该集合进行操作，又需要遍历整张图中的，每条边，复杂度也为O(E+V);

因此Kahn算法的复杂度即为O(E+V)。

基于DFS的拓扑排序：

除了使用上面直观的Kahn算法之外，还能够借助深度优先遍历来实现拓扑排序。这个时候需要使用到栈结构来记录拓扑排序的结果。

同样摘录一段维基百科上的伪码：

L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
    visit(n) 
function visit(node n)
    if n has not been visited yet then
        mark n as visited
        for each node m with an edgefrom m to ndo
            visit(m)
        add n to L

DFS的实现更加简单直观，使用递归实现。利用DFS实现拓扑排序，实际上只需要添加一行代码，即上面伪码中的最后一行：add n to L。

需要注意的是，将顶点添加到结果List中的时机是在visit方法即将退出之时。

这个算法的实现非常简单，但是要理解的话就相对复杂一点。

关键在于为什么在visit方法的最后将该顶点添加到一个集合中，就能保证这个集合就是拓扑排序的结果呢？

因为添加顶点到集合中的时机是在dfs方法即将退出之时，而dfs方法本身是个递归方法，只要当前顶点还存在边指向其它任何顶点，它就会递归调用dfs方法，而不会退出。因此，退出dfs方法，意味着当前顶点没有指向其它顶点的边了，即当前顶点是一条路径上的最后一个顶点。

 

下面简单证明一下它的正确性：

考虑任意的边v->w，当调用dfs(v)的时候，有如下三种情况：

1. dfs(w)还没有被调用，即w还没有被mark，此时会调用dfs(w)，然后当dfs(w)返回之后，dfs(v)才会返回

1. dfs(w)已经被调用并返回了，即w已经被mark

1. dfs(w)已经被调用但是在此时调用dfs(v)的时候还未返回

需要注意的是，以上第三种情况在拓扑排序的场景下是不可能发生的，因为如果情况3是合法的话，就表示存在一条由w到v的路径。而现在我们的前提条件是由v到w有一条边，这就导致我们的图中存在环路，从而该图就不是一个有向无环图(DAG)，而我们已经知道，非有向无环图是不能被拓扑排序的。

 

那么考虑前两种情况，无论是情况1还是情况2，w都会先于v被添加到结果列表中。所以边v->w总是由结果集中后出现的顶点指向先出现的顶点。为了让结果更自然一些，可以使用栈来作为存储最终结果的数据结构，从而能够保证边v->w总是由结果集中先出现的顶点指向后出现的顶点。

实现代码：

 public class DirectedDepthFirstOrder
 {
     // visited数组，DFS实现需要用到
     private boolean[] visited;
     // 使用栈来保存最后的结果
     private Stack<Integer> reversePost;

     /**
      * Topological Sorting Constructor
      */
     public DirectedDepthFirstOrder(Digraph di, boolean detectCycle)
     {
         // 这里的DirectedDepthFirstCycleDetection是一个用于检测有向图中是否存在环路的类
         DirectedDepthFirstCycleDetection detect = new DirectedDepthFirstCycleDetection(
                 di);

         if (detectCycle && detect.hasCycle())
             throw new IllegalArgumentException("Has cycle");

         this.visited = new boolean[di.getV()];
         this.reversePost = new Stack<Integer>();

         for (int i = 0; i < di.getV(); i++)
         {
             if (!visited[i])
             {
                 dfs(di, i);
             }
         }
     }

     private void dfs(Digraph di, int v)
     {
         visited[v] = true;

         for (int w : di.adj(v))
         {
             if (!visited[w])
             {
                 dfs(di, w);
             }
         }

         // 在即将退出dfs方法的时候，将当前顶点添加到结果集中
         reversePost.push(v);
     }

     public Iterable<Integer> getReversePost()
     {
         return reversePost;
     }
 }

复杂度分析：

复杂度同DFS一致，即O(E+V)。具体而言，首先需要保证图是有向无环图，判断图是DAG可以使用基于DFS的算法，复杂度为O(E+V)，而后面的拓扑排序也是依赖于DFS，复杂度为O(E+V)

 

还是对上文中的那张有向图进行拓扑排序，只不过这次使用的是基于DFS的算法，结果是：

8->7->2->3->0->6->9->10->11->12->1->5->4

两种实现算法的总结：

这两种算法分别使用链表和栈来表示结果集。

对于基于DFS的算法，加入结果集的条件是：顶点的出度为0。这个条件和Kahn算法中入度为0的顶点集合似乎有着异曲同工之妙，这两种算法的思想犹如一枚硬币的两面，看似矛盾，实则不然。一个是从入度的角度来构造结果集，另一个则是从出度的角度来构造。

 

实现上的一些不同之处：

Kahn算法不需要检测图为DAG，如果图为DAG，那么在出度为0的集合为空之后，图中还存在没有被移除的边，这就说明了图中存在环路。而基于DFS的算法需要首先确定图为DAG，当然也能够做出适当调整，让环路的检测和拓扑排序同时进行，毕竟环路检测也能够在DFS的基础上进行。

二者的复杂度均为O(V+E)。

 

环路检测和拓扑排序同时进行的实现：

 public class DirectedDepthFirstTopoWithCircleDetection
 {
     private boolean[] visited;
     // 用于记录dfs方法的调用栈，用于环路检测
     private boolean[] onStack;
     // 用于当环路存在时构造之
     private int[] edgeTo;
     private Stack<Integer> reversePost;
     private Stack<Integer> cycle;

     /**
      * Topological Sorting Constructor
      */
     public DirectedDepthFirstTopoWithCircleDetection(Digraph di)
     {
         this.visited = new boolean[di.getV()];
         this.onStack = new boolean[di.getV()];
         this.edgeTo = new int[di.getV()];
         this.reversePost = new Stack<Integer>();

         for (int i = 0; i < di.getV(); i++)
         {
             if (!visited[i])
             {
                 dfs(di, i);
             }
         }
     }

     private void dfs(Digraph di, int v)
     {
         visited[v] = true;
         // 在调用dfs方法时，将当前顶点记录到调用栈中
         onStack[v] = true;

         for (int w : di.adj(v))
         {
             if(hasCycle())
             {
                 return;
             }
             if (!visited[w])
             {
                 edgeTo[w] = v;
                 dfs(di, w);
             }
             else if(onStack[w])
             {
                 // 当w已经被访问，同时w也存在于调用栈中时，即存在环路
                 cycle = new Stack<Integer>();
                 cycle.push(w);
                 for(int start = v; start != w; start = edgeTo[start])
                 {
                     cycle.push(v);
                 }
                 cycle.push(w);
             }
         }

         // 在即将退出dfs方法时，将顶点添加到拓扑排序结果集中，同时从调用栈中退出
         reversePost.push(v);
         onStack[v] = false;
     }

     private boolean hasCycle()
     {
         return (null != cycle);
     }

     public Iterable<Integer> getReversePost()
     {
         if(!hasCycle())
         {
             return reversePost;
         }
         else
         {
             throw new IllegalArgumentException("Has Cycle: " + getCycle());
         }
     }

     public Iterable<Integer> getCycle()
     {
         return cycle;
     }
 }

拓扑排序解的唯一性：

哈密顿路径：

哈密顿路径是指一条能够对图中所有顶点正好访问一次的路径。本文中只会解释一些哈密顿路径和拓扑排序的关系，至于哈密顿路径的具体定义以及应用，可以参见本文开篇给出的链接。

 

前面说过，当一个DAG中的任何两个顶点之间都存在可以确定的先后关系时，对该DAG进行拓扑排序的解是唯一的。这是因为它们形成了全序的关系，而对存在全序关系的结构进行线性化之后的结果必然是唯一的(比如对一批整数使用稳定的排序算法进行排序的结果必然就是唯一的)。

 

需要注意的是，非DAG也是能够含有哈密顿路径的，为了利用拓扑排序来实现判断，所以这里讨论的主要是判断DAG中是否含有哈密顿路径的算法，因此下文中的图指代的都是DAG。

 

那么知道了哈密顿路径和拓扑排序的关系，我们如何快速检测一张图是否存在哈密顿路径呢？

根据前面的讨论，是否存在哈密顿路径的关键，就是确定图中的顶点是否存在全序的关系，而全序的关键，就是任意一对顶点之间都是能够确定先后关系的。因此，我们能够设计一个算法，用来遍历顶点集中的每一对顶点，然后检查它们之间是否存在先后关系，如果所有的顶点对有先后关系，那么该图的顶点集就存在全序关系，即图中存在哈密顿路径。

 

但是很显然，这样的算法十分低效。对于大规模的顶点集，是无法应用这种解决方案的。通常一个低效的解决办法，十有八九是因为没有抓住现有问题的一些特征而导致的。因此我们回过头来再看看这个问题，有什么特征使我们没有利用的。还是举对整数进行排序的例子：

比如现在有3， 2， 1三个整数，我们要对它们进行排序，按照之前的思想，我们分别对(1,2)，(2,3)，(1,3)进行比较，这样需要三次比较，但是我们很清楚，1和3的那次比较实际上是多余的。我们为什么知道这次比较是多余的呢？我认为，是我们下意识的利用了整数比较满足传递性的这一规则。但是计算机是无法下意识的使用传递性的，因此只能通过其它的方式来告诉计算机，有一些比较是不必要的。所以，也就有了相对插入排序，选择排序更加高效的排序算法，比如归并排序，快速排序等，将n2的算法加速到了nlogn。或者是利用了问题的特点，采取了更加独特的解决方案，比如基数排序等。

 

扯远了一点，回到正题。现在我们没有利用到的就是全序关系中传递性这一规则。如何利用它呢，最简单的想法往往就是最实用的，我们还是选择排序，排序后对每对相邻元素进行检测不就间接利用了传递性这一规则嘛？所以，我们先使用拓扑排序对图中的顶点进行排序。排序后，对每对相邻顶点进行检测，看看是否存在先后关系，如果每对相邻顶点都存在着一致的先后关系(在有向图中，这种先后关系以有向边的形式体现，即查看相邻顶点对之间是否存在有向边)。那么就可以确定该图中存在哈密顿路径了，反之则不存在。

 

实现代码：

 /**
  * Hamilton Path Detection for DAG
  */
 public class DAGHamiltonPath
 {
     private boolean hamiltonPathPresent;
     private Digraph di;
     private KahnTopological kts;

     // 这里使用Kahn算法进行拓扑排序
     public DAGHamiltonPath(Digraph di, KahnTopological kts)
     {
         this.di = di;
         this.kts = kts;

         process();
     }

     private void process()
     {
         Integer[] topoResult = kts.getResultAsArray();

         // 依次检查每一对相邻顶点，如果二者之间没有路径，则不存在哈密顿路径
         for(int i = 0; i < topoResult.length - 1; i++)
         {
             if(!hasPath(topoResult[i], topoResult[i + 1]))
             {
                 hamiltonPathPresent = false;
                 return;
             }
         }
         hamiltonPathPresent = true;
     }

     private boolean hasPath(int start, int end)
     {
         for(int w : di.adj(start))
         {
             if(w == end)
             {
                 return true;
             }
         }
         return false;
     }

     public boolean hasHamiltonPath()
     {
         return hamiltonPathPresent;
     }
 }