Knight Moves（第一次写的双向优先BFS）

Link：http://poj.org/problem?id=1915

Problem：

Knight Moves

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 22079		Accepted: 10314

Description

Background 
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him? 
The Problem 
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov. 
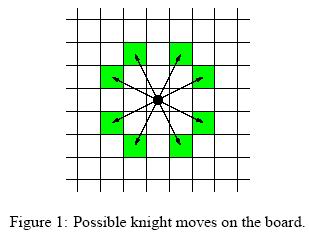
For people not familiar with chess, the possible knight moves are shown in Figure 1. 

Input

The input begins with the number n of scenarios on a single line by itself. 
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.

Output

For each scenario of the input you have to calculate the minimal amount of knight moves which are necessary to move from the starting point to the ending point. If starting point and ending point are equal,distance is zero. The distance must be written on a single line.

Sample Input

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

Sample Output

5
28
0

Source

TUD Programming Contest 2001, Darmstadt, Germany

#include <algorithm>
#include <bitset>
#include <cassert>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <functional>
#include <iomanip>
#include <iostream>
#include <list>
#include <map>
#include <queue>
#include <set>
#include <sstream>
#include <stack>
#include <string>
#include <vector>
using namespace std;    //}

int vis[333][333];
int d[8][2] = {{ -1, -2}, { -2, -1}, { -2, 1}, {1, -2}, { -1, 2}, {2, -1}, {1, 2}, {2, 1}};
int n;

struct node {
    int r;
    int c;
    int sp;
} st, ed;

int DBFS() {
    memset(vis, 0, sizeof(vis));
    queue<node> Q1, Q2;
    st.sp = 0;
    ed.sp = 0;
    Q1.push(st);
    vis[st.r][st.c] = 1;
    Q2.push(ed);
    vis[ed.r][ed.c] = 2;
    node now, next;
    int qi, i, n1 = 0, n2 = 0;

    while(!Q1.empty()||!Q2.empty()){
        if(Q1.size() <= Q2.size())
            qi = 1;
        else
            qi = 2;

        if (Q1.front().sp+1==n1) qi=1;//很容易写漏了这两行，要注意！！！
        if (Q2.front().sp+1==n2) qi=2;

        if(qi == 1) {
            now = Q1.front();
            n1 = now.sp + 1;
            Q1.pop();

            for(i = 0; i < 8; i++) {
                next.c = now.c + d[i][1];
                next.r = now.r + d[i][0];

                if(next.c < 0 || next.r >= n || next.c >= n || next.r < 0)
                    continue;

                if(vis[next.r][next.c] == 0) {
                    next.sp = now.sp + 1;
                    Q1.push(next);
                    vis[next.r][next.c] = 1;
                }

                if(vis[next.r][next.c] == 2) {
                    return n1 + n2;
                }
            }
        }

        if(qi == 2) {
            now = Q2.front();
            n2 = now.sp + 1;
            Q2.pop();

            for(i = 0; i < 8; i++) {
                next.c = now.c + d[i][1];
                next.r = now.r + d[i][0];

                if(next.c < 0 || next.r >= n || next.c >= n || next.r < 0)
                    continue;

                if(vis[next.r][next.c] == 0) {
                    next.sp = now.sp + 1;
                    Q2.push(next);
                    vis[next.r][next.c] = 2;
                }

                if(vis[next.r][next.c] == 1) {
                    return n1 + n2;
                }
            }
        }

    }
}
int main() {
    int cas, ans;

    while(scanf("%d", &cas) != EOF) {
        while(cas--) {
            scanf("%d", &n);
            scanf("%d%d", &st.r, &st.c);
            scanf("%d%d", &ed.r, &ed.c);

            if(st.c == ed.c && st.r == ed.r)
                printf("0\n");
            else {
                ans = DBFS();
                printf("%d\n", ans);
            }
        }
    }

    return 0;
}

经验总结：很感谢一位叫“代号4101”的学长的指点，让我找到了一个隐藏很深的Bug！！！在自己写的代码后添加以下这两行，才AC了，之前没注意到一直郁闷过不了~~

        if (Q1.front().sp+1==n1) qi=1;
        if (Q2.front().sp+1==n2) qi=2;

添加这两行的意思是：就是每次要pop完同一层的所有节点后才能去选择节点数少的队列优先搜索，不能只pop一个Q1或Q2的点！！！

例如：

 如果Q1队列里有3个sp为2的点ABC，Q2有2个sp为3的点DE,n1=2,n2=3

那么现在D出队，n2为4了，D搜到了FGHI四个点

下一次循环A出队，A搜到了与E相同的点

那会怎样？你的程序算出是多少？实际值是多少？

没添加这两行代码的程序计算是，当前n1=3，n2=4，所以输出7
但实际值应该是6！！！

顺便贴上别人写的：

单队列`双向广搜

POJ 1915 【单队列`双向广搜】【模板】  

2013-08-22 23:06:54|  分类： Moving... |  标签：搜索  dbfs  模板  |举报|字号 订阅

【 POJ 1915 题意】 

可以参照象棋里“马”的走法，有8个方向。

给定起点、终点，求从起点到终点所花的最少步数。

【思路】

比较直观的是直接上BFS，但是可以用来练习简单的双向广搜(DBFS)。

这里是将向前和向后扩展的结点存在同一个队列里面，

根据点在队列里是离散存储的原理，可用 用不同的标记来扩展结点。

【复杂度】

//Memory: 1180K

Time: 407MS

【源码】

//poj 1915 【单队列DBFS】

#include<stdio.h>

#include<stdlib.h>

#include<queue>

#include<string.h>

#include<math.h>

#include<algorithm>

#define N 350

using namespace std;

int dirx[8]={1,2,2,1,-1,-2,-2,-1};

int diry[8]={2,1,-1,-2,-2,-1,1,2};

int step[N][N];

int vis[N][N];

int n;

struct node 

{

int x,y;

}s,e;

int dbfs()

{

int i,j;

queue<node> que;

node next,cur;

step[s.x][s.y]=step[e.x][e.y]=0;

vis[s.x][s.y]=1;//由起点开始扩展的标记为1

vis[e.x][e.y]=2;//由终点开始扩展的标记为2

que.push(s);

que.push(e);

while(!que.empty())

{

cur=que.front();

que.pop();

for(i=0;i<8;i++)

{

next.x=cur.x+dirx[i];

next.y=cur.y+diry[i];

if(next.x>=0&&next.y>=0&&next.x<n&&next.y<n)

{

if(vis[next.x][next.y]==0)//没有访问过

{

step[next.x][next.y]=step[cur.x][cur.y]+1;

vis[next.x][next.y]=vis[cur.x][cur.y];//由cur扩展出去的结点标记做相同标记

que.push(next);

}

else if(vis[next.x][next.y]!=vis[cur.x][cur.y])//当cur和由其扩展的结点标记不同时就【相遇】

{

return step[next.x][next.y]+step[cur.x][cur.y]+1;

}

}

}

}

}

int main()

{

int i,j,m,t;

scanf("%d",&t);

while(t--)

{

memset(step,0,sizeof(step));

memset(vis,0,sizeof(vis));

scanf("%d",&n);

scanf("%d%d%d%d",&s.x,&s.y,&e.x,&e.y);

if(s.x==e.x&&s.y==e.y)    puts("0");

else    printf("%d\n",dbfs());

}

return 0;

}//如果是要求保存路径的题目就模拟队列保存前驱