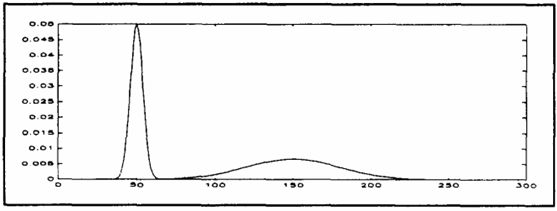
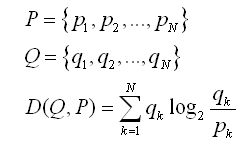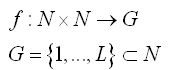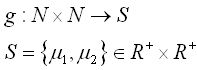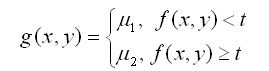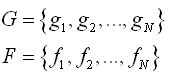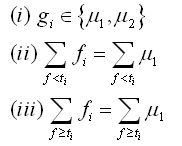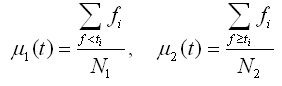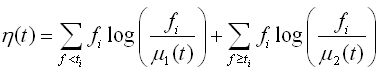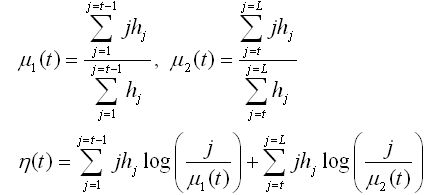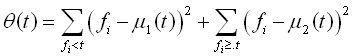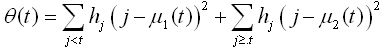最小交叉熵圖像分割（Minimum cross entropy thresholding）

http://blog.csdn.net/likezhaobin/article/details/6937569

本文是Li和Lee關於一維最小交叉熵圖像閾值分割的原文。這裡進行了簡單翻譯，有不足的地方請大家一起討論完善。後續有文章對信息熵學進行初窺，敬請期待。

摘要：通過最小化圖像與其部分區域之間的交叉熵解決了圖像分割中的閾值選取問題。其中交叉熵基於兩幅圖像之間的像素運算得到，同時提出一種基於統計直方圖的實現算法。該方法提出了一種信息理論意義上針對二值圖像的無偏估計，因而不需要了解圖像灰度分布的先驗知識。

1、介紹

      在眾多的模式識別系統中，圖像閾值化是重要的一個初步環節。其中閾值的選取會影響到後期圖像分割的精度以及效率。本文的方法假設圖像中的背景和待分割目標可以通過將圖像的灰度值與選定的一個合適的閾值對比而區分。分割圖像可能不適合作為通常意義上的圖像處理例程的輸入，因為在空間范圍內它缺少對圖像像素的更多有效信息。盡管如此，這種閾值化算法實現簡單並且運行速度高，這使得它成為目前包括從醫學英語到工業制造的眾多自動化系統中使用最廣泛的算法。二值化圖像同樣很適合在硬件上通過相關性以及實時識別進行模板匹配處理。除了在圖像分割中全局閾值化的應用外，這種方法同樣可以用於模式識別領域的眾多分類問題中。

      關於閾值選取研究工作的詳細總數可以在參考文獻1-3中找到。通常來說，閾值選取算法可以根據算法的性質粗略劃分為全局方法和局部方法。局部閾值化算法基於直方圖函數的局部屬性來選取閾值，比如根據存在的極大值和極小值。一個典型局部閾值化算法的例子是基於直方圖局部最小值定位的谷底（thebottom of the valley approach）算法。從原理上講，這種方法依賴於灰度差值因此對噪聲比較敏感。因而在這個過程中很重要的預處理就是對圖像及其直方圖進行平滑。此外，往往當地的極值點不一定保證存在，這時可采用直方圖增強或者銳化算法用來克服解決這些困難。局部閾值化算法的一個優點就是它不需要先驗知識就可以確定類別的數量。全局閾值化算法則是通過對直方圖進行全局統計而得到選取標准。這種方法降低了對噪聲的敏感度並且不需要進行圖像增強，這些增強通常對單個的圖像特征很敏感並且需要監督。最近以來，Wilson和Spann介紹了一種將局部閾值化方法和全局閾值化方法結合起來的集群算法，這種算法消除了以上大多數的不足之處。在本文中，作者僅討論全局閾值化方法，同時采用目前使用最廣的兩種算法進行了對比：Kittler與Illingworth提出的最小誤差閾值算法以及Ostu算法。在大津算法中，閾值的選取是通過最大化類間方差實現的，這種方法基於類內的方差，類間方差以及整個灰度級的全局方差。該方法不需要輸入參數，無需監督並且無需先驗知識。該方法目前應用廣泛，並且通常被當做標准算法與其他閾值算法結果進行比較。其主要不足是當兩個基本分布存在不同方差時或者兩個分布所包含元素數有較大不同時，該方法在閾值估計上存在偏差。

      在最小誤差算法中，包括目標和背景的像素集都假定為正態分布。閾值選取的准則是使得像素集之間的平均誤差最小。除了假設正態分布外，該方法還假設兩個總體分布重疊較小同時推倒中所產生的截斷誤差可忽略。該方法試圖繞過對直方圖中兩個分布均值，方差以及標准差的估計。當灰度確實是正態分布時該方法可以對閾值給出較好的估計，而當分布為單峰的正態分布時，該方法不能給出閾值估計。Cho等人對最小誤差算法提出了改進，他們對截斷造成的方差估計偏差進行了修正。由於建模的原理都是一致的，我們將參考文獻5作為基礎進行討論和比較。

以上兩個算法是將統計直方圖作為唯一輸入的的閾值化算法的代表。另外一類的閾值化算法同樣僅僅使用到了統計直方圖，這些方法應用到了包括圖像分割問題的最大熵值原理。這些方法用到了信息理論中熵的概念，其不用明確參考圖像屬性，比如二維分布以及在實際應用中有顯著的限制。算法細節將在第3部分討論。

2、最大熵原理

      最大熵原理最早由Jaynes提出來，用於估計限制條件下的未知概率分布。這些限制的作用是將解決方案集限制在只包括與數據相一致的解決方案范圍內。推理問題常常因為數據不足而變得不確定，因此在應用了所有的限制條件後，往往還有多種解決方案存在。最大熵值原理允許我們選擇給出最大熵值（信息）的方案。最初的想法是它將會給出無偏的估計，並且在限制范圍內允許最大的自由度。這些年來，最大熵理論經歷了廣泛的理論辯論並且已經成功的應用到了科學與工程的多個領域。濃度定理（ConcentrationTheorem）和多重性的研究表明，更高的熵值具有更好的多重性，因而更易被觀測到。顯而易見的，在新信息以期望值給定的時候最大熵值方法是歸納推理的唯一正確方法。它被延伸到一般的推理方法，用於處理包括非相干圖像強度或者功率譜密度的分布等領域。總的來說，該方法已經被廣泛應用於各種領域並且證明是成功的。例如，在譜估計領域，最大熵可以提供比傳統估計方法如極大似然法更高的分辨率。

      Kullback提出交叉熵的時候命名為定向差異（directed divergence）。交叉熵測量兩個分布P和Q之間的信息理論距離，其中定義如下：

公式（1）

      Renyi等人同樣對D的測量進行了研究，他們將D看做這兩個分布之間的信息理論距離。Renyi還指出當我們用Q取代P時，此公式可解釋為信息內容變化的期望。最小交叉熵方法可以看做是最大熵法的擴展，條件是為上公示中所有的p設置相等的初始估計，並且沒有先驗信息存在。

3、最小交叉熵分割法

      對於投擲篩子這樣一個實驗來說，每次投擲是一個單獨的事件，不會影響其他投擲的結果，熵最大化會導致不同投擲的獨立結果概率。盡管如此，對於時間序列分析或者圖像建模來說，數據間有較強的聯系，為了考慮相互之間的信息內容，模型必須將時間序列或者圖像作為一個單一的抽樣，同時將最大熵原理的組合參數應用到許多不同抽樣試驗中。

      將最大熵方法用於圖像分割，之前的研究工作沒有考慮上述的區別並且將像素產生的過程看做是獨立試驗。他們基於具有一定灰度級單個像素的隨機試驗和測量像素分布的熵，將歸一化的灰度直方圖作為灰度級的概率分布。Kapur提出的最大熵閾值化方法被認為由於其他的熵譜閾值算法。盡管如此，最大熵方法仍然沒有被很好接受，並且性能較差，因而有大量工作對其進行了改進。Wong和Sahoo結合圖像中的空間信息和熵來產生閾值選取標准。在最大熵值方法中保留了直方圖熵函數的同時，Kapur介紹了一系列附加的啟發式原則來選擇閾值。綜上可知，不采用附加准則而僅僅通過熵原理制定通用的直方圖閾值算法是不成功。

      在計劃中，分割過程是一個圖像分布重建的過程。考慮圖像函數如下：

      其中N是正整數，G為灰度集合。分割過程就是重建如下函數:

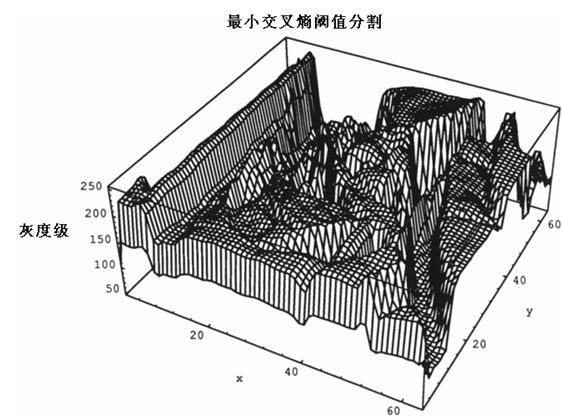
      其中的R+是正的實整數。圖1和圖2展現了一個源圖像f(x,y)和一個分割圖像g(x,y)，其中坐標系的z軸代表了圖像的灰度級。分割圖像g(x,y)將按照下式進行重構：

公式（2）

      

圖1 灰度圖像的三維圖（Z為灰度級）

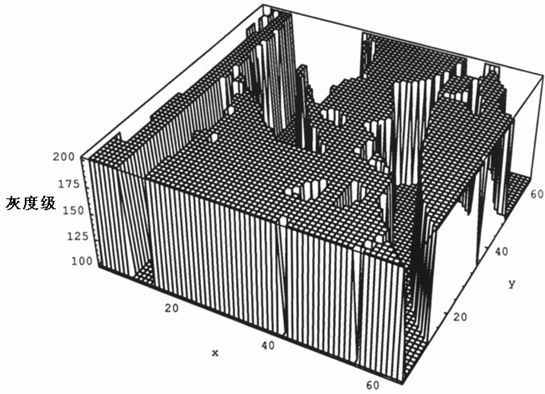
圖2 分割圖像的三維圖

      此分割圖像g(x,y)來自f(x,y)，具體形式由三個未知的參數決定。必須建立准則來尋找最有的g，或者等價的三個參數，使其盡可能的與f相似。可表達如下：

公式（3）

      准則函數一般是某種失真測量，例如從f到g的均方根差時常用的措施。最小誤差法和大津法都屬於這種方法。在這一章的結尾，我們將會展示大津法最小化圖像和分割區域之間的最小均方差，而我們提出的是最小化交叉熵方法。交叉熵法沒有采用均方差，這種方法注重對正像分布的測量。

      上面提出的問題可以作為一個帶限制條件的經典的最大熵推理問題。對問題重述如下：

      G為一系列的值，N是圖像中的像素點個數，F為源圖像，現在要根據F和可用的限制條件來求得G向量。這裡用相同的方式通過線性化2維分布得到新的分布，因此G和F中的元素來自圖像空間同樣的像素位置，同時G包括了只有兩個值的元素，該元素目前還未知。接下來，將要用到強度保護約束。由於我們想要重建圖像的分布，觀測圖像強度F會給G中的兩個元素帶來約束，這樣使得重建圖像中總的強度與觀測圖像相等。限制表達式如下：

公式（4）

      這樣，該兩個參數可以由如下公式來確定：

公式（5）

      其中N1和N2分別為兩個區域內的像素點個數。聯合以上公式1、2和5可以得到：

公式（6）

      閾值可以選取為：

公式（7）

      其中t0即為所需要的門限值。以上的和在整幅圖像上進行，盡管如此，有一些可替換的計算可分類。這樣就得到了如下的公式：

公式（8）

       以上模型中的交叉熵的形式看起來和Skilling推倒的圖像分割方法很相似，在他的方法中用到了4個公理推出如下的熵函數：

公式（9）

      其中 f(x)是圖像強度分布函數，m(x)是圖像模型。實際上，如果包括總的強度轉換限制，這兩個方程只差一個符號，因為8公式中的兩個積分在整個類上積分將會抵消。

      以上的方法介紹了最小化圖像和分割區域之間的交叉熵。大津法最小化類間方差也可以從以上的方法中推導出來，這要用到兩幅圖像之間的均方差並且如4式所示的同樣的限制。這樣標准函數就變為如下形式：

公式（10）

      用直方圖進行分類，標准函數就如下所示：

公式（11）

      類內方差6式進行了定義，最小化11式所定義的函數等效於最大化大津法的准則，因為類內方差以及類間方差的和與選擇的閾值相獨立。

      交叉熵函數的使用不僅僅限於閾值圖像分割。結合其他的限制，可以將該算法擴展到圖像分割的其他領域。例如，有些基於區域的分割方法就用交叉熵作為准則，比如分裂與合並方法，合並的地區可根據空間坐標標簽的限制來確定。

4、算法的應用和討論

      為了進行對比，這裡采用Kittler和Illingworth提出的算法，大津算法，最小誤差方法以及最小交叉熵算法被用於參考文獻5所討論的正態分布。這些直方圖如圖3-5所示。我們同樣采用了真實工業圖像的直方圖。根據這些方法所選擇的閾值在表1中展示。

圖3 直方圖a

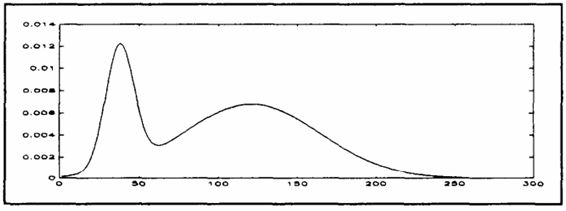
圖4 直方圖b

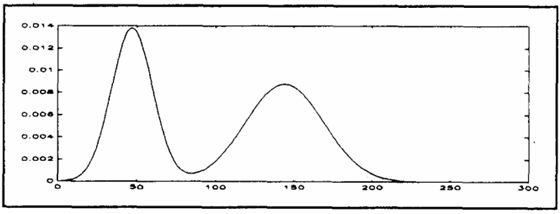
圖5 直方圖c

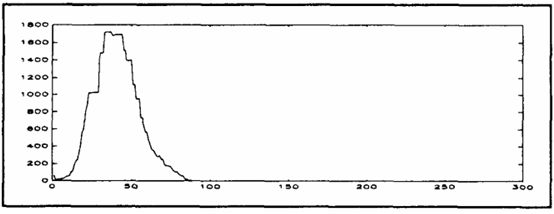
圖6 直方圖d

      前三個直方圖的對高斯分布結果可以總結為：最小誤差方法將正態分布作為模型，隨後優於最小交叉熵和大津算法。盡管如此，最小交叉熵能夠給出一個優化的閾值，這個數值相比大津算法和最大熵算法更加接近於最有的閾值。

      對於圖7所示的勞損測量圖像，我們的目標是測量橢圓形的主軸和次軸的變化，這些將會給出金屬的應變信息。第一步是進行平行線和橢圓從背景中的分割。直方圖被提取出來如圖6所示。最小誤差法沒有給出任何閾值信息，因為針對該標准函數沒有內部最小值存在。直方圖將其錯誤的推斷為單峰，而實際情況是這兩個分布因為有大量噪聲而高度重疊。這表明錯誤的假設可能是災難性的。最小交叉熵方法和大津法能成功的選取閾值，相比其他方法該閾值能夠使得分割圖像有較低的噪聲水平。

      為了進行證明，對比圖8和圖9、圖10，圖8顯示了最小交叉熵法的分割圖像（選定的閾值為40），圖9和圖10分別顯示了小於40與大於40時的分割圖像。圖9中出現了更多的洞，還有開裂的線條以及橢圓。圖示包括了太多的背景。這說明了選擇正確的閾值是很關鍵的，因為他將產生高度重疊的分布。

 

      關於最後測試的圖，詳見作者原文。可從我的資源裡面下載， 點擊這裡 。