并查集经典扩展-pku1182(食物链)-并查集用于等价类问题

 

并查集的普通应用包括，计算最小生成树的kruscal算法和无向图的连通性问题。

这个题目是并查集的一个扩展应用，用于解决等价类问题。

 

 

问题描述:

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。 
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。 
有人用两种说法对这N个动物所构成的食物链关系进行描述： 
第一种说法是"1 X Y"，表示X和Y是同类。 
第二种说法是"2 X Y"，表示X吃Y。 
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。 
1） 当前的话与前面的某些真的话冲突，就是假话； 
2） 当前的话中X或Y比N大，就是假话； 
3） 当前的话表示X吃X，就是假话。 
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。 

输入:

第一行是两个整数N和K，以一个空格分隔。 
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。 
若D=1，则表示X和Y是同类。 
若D=2，则表示X吃Y。

输出:

只有一个整数，表示假话的数目。

 

 

算法思路：

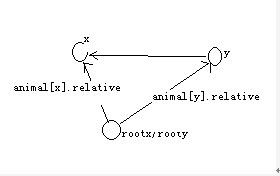
在原有parent[]的基础上加上另一关系relative[x],用于表示动物x相对于其根节点的关系:

1.      如果relative[x]=0, 说明x和根节点的关系是同类

2.      如果relative[x]=1, 说明x和根节点的关系是x吃根节点

3.      如果relative[x]=2, 说明x被根节点吃。

 

由于再输入的时候也会输入x和y的关系D，题目中说D=1表示x和y是同类，D=2表示x吃y，与relative[]关系表示有出入，所以在输入D之后要做一写调整D-1。

 

 

#include <iostream> #include <stdio.h> #include <stdlib.h> using namespace std; struct { int relative; //如果relative ==0,说明这个动物相对于根节点是同类，relative = 1,说明该动物相对于根节点是吃的关系，如果relative= 2，被吃的关系 int parent; }animal[50010]; void MakeSet(int SizeOfSet) { //初始化并查集，将每个结点的根结点设置为自己 //相互之间关系确定的结点才放入一个集合里 //一句话都没有输入之前所有节点之间的关系都不确定，所以各自单独一个集合 //每个结合的根节点relative都是0，有利于合并时relative值的计算 for (int i = 0;i < SizeOfSet;i++) { animal[i].parent = i; animal[i].relative = 0; } } void Union(int RootOfX,int RootOfY,int NodeX,int NodeY,int D) { //此函数作用:1.将Y的根节点的根节点设置为X的根结点 //2.由于设置后RootOfY已经不再是根节点，所以要保证其kind相对于RootOfX的正确性 //在此函数里，D==0说明NodeX与NodeY同类， //D==1说明NodeX吃NodeY，因此传参前要将D减一 //将Y所在树依附到X所在树上 animal[RootOfY].parent = RootOfX; //更新RootOfY的kind，保证其kind相对于RootOfX的正确性 //原始公式为animal[NodeX].relative-(animal[NodeY].relative+amimal[RootOfY].relative)=D; animal[RootOfY].relative = (-D+(animal[NodeX].relative-animal[NodeY].relative)+3)%3; } int Find(int NodeToFind) { //此函数作用：1找到NodeToFind所在集合，即找到其根节点 //2.查找的过程是一个递归过程，递归出口是遇到一个根节点为自身的结点，即当前集合的根节点 //然后递归返回的路径上依次将各个各个结点的根节点设置为此节点，并继续返回此根结点，这样就可以 //把集合中所有结点的根节点设置为同一个根结点，这叫做“路径压缩”， //是为了使并查集稳定而做的一种改进，目的是避免并查集成为接近于链表的结构，因为并查集的优势体现在 //树的深度较浅，查找容易，此举可看作对并查集深度的控制。 //递归返回路径上，除了要做更新途径结点（按照距根从近到远的顺序）的根结点外，还要依次修正 //途径结点的relative。这是因为在Union操作中只是保证了直接和根节点相连的 //结点（即未作Union操作前的某一树的根）relative的正确性，其他节点kind的正确性就需要在这里修正 //从近到远进行修正恰好保证了每次修正都有理有据。 //每次修正都要依仗其原根节点relative的正确性，因为这是一个相对计算的关系 if(animal[NodeToFind].parent==NodeToFind) return NodeToFind; int temp = animal[NodeToFind].parent; animal[NodeToFind].parent = Find(animal[NodeToFind].parent); //更新NodeToFind结点kind的正确性，因为原来的kind是相对于0（根节点relative都为0）， //原来的根节点现在已经不是根节点了，所以只需要根据原根节点现有的kind值即可更新 animal[NodeToFind].relative = (animal[NodeToFind].relative+animal[temp].relative+3)%3; return animal[NodeToFind].parent; } int main() { int n,k; cin>>n>>k; MakeSet(n); int x,y,d; int NumOfLies = 0; while (k--) { //cin>>d>>x>>y; //cin导致TLE scanf("%d%d%d",&d,&x,&y); //cin >> d >> x >> y; if(x>n||y>n) NumOfLies++; else if(x==y&&d==2) NumOfLies++; else { int rootx = Find(x); int rooty = Find(y); if (rootx==rooty) { //如果两节点的根相等，说明根据以往结论，这两点的关系已经确定，可以开始判断 if(d==1&&animal[x].relative!=animal[y].relative) NumOfLies++; if(d==2&&(animal[x].relative-animal[y].relative+3)%3!=d-1) NumOfLies++; } else { //x和y不在一个集合里，说明两者关系尚未确定，则将两者关系进行确定， //即将两者所在集合进行合并操作Union，Union操作只保证了和根结点相连的结点kind //的正确性，不要担心，由于并查集的特点（根节点表示法的树）所以无法从根向下找到 //子节点，因此子节点即使有错误也是安全的，到了需要访问（Find）的时候再修正也不迟 Union(rootx,rooty,x,y,d-1); //别忘了d要减一才符合我们规定的含义 } } } cout<<NumOfLies<<endl; for(int i= 0; i< n; i++) { cout << i << ' '<< animal[i].parent<<' '<< animal[i].relative << endl; } }  

 

 

下面对比较难理解的地方进行讲解：

1.

在main（）函数中 else { int rootx = Find(x); int rooty = Find(y); if (rootx==rooty) { if(d==1&&animal[x].relative!=animal[y].relative) NumOfLies++; if(d==2&&(animal[x].relative-animal[y].relative+3)%3!=d-1) NumOfLies++; } else Union(rootx,rooty,x,y,d-1); } } }

 

首先通过find（）函数找出x和y的根节点rootx和rooty, 

如果rootx和rooty相等，那么说明x和y的关系在原来语句的基础上是可以判断对错的，if(d==1&&animal[x].relative!=animal[y].relative) 如果输入的关系是d=1,说明这句话表明x和y是同类，而通过判断animal[x].relative与animal[y].relative是否是同类，如果animal[x].relative！=animal[y].relative说明在原来语句的基础上推出x和y不是同类，这样就与当前这个语句矛盾了，所以错误数++。

if(d==2&&(animal[x].relative-animal[y].relative+3)%3!=1)，如果输入关系d=2，说明x是吃y的，也就是说x相对于y的关系是1，那么怎么从以前语句中推出x和y的关系呢？是(animal[x].relative-animal[y].relative+3)%3，具体解释得通过向量关系来推导：

 

 

 

x相对于rootx的关系向量是animal[x].relative,y相对于rooty的关系向量是animal[y].relative，要求出x相对于y的关系，=》(animal[x].relative-animal[y].relative+3)%3,如果这个值和1不相等，也就是说以前的语句和当前语句矛盾，所以错误数++.

如果rootx和rooty不相等，说明x和y的关系在原有语句的基础上是不能确定的，于是我们就认为这个语句是正确的，于是调用Union(rootx,rooty,x,y,d-1);把x节点的树和y节点的树合并。注意这里为什么是d-1，是因为在前面解释了。

 

2.

在union()函数中做的修改： void Union(int RootOfX,int RootOfY,int NodeX,int NodeY,int D) { animal[RootOfY].parent = RootOfX; animal[RootOfY].relative = (-D+(animal[NodeX].relative-animal[NodeY].relative)+3)%3; }  

 

在union（）函数中，除了要对树rootx和树rooty进行合并，同时还要对rooty节点的relative做修改。

这里直接就是把rooty的parent指向了rootx.

 

虽然parent关系已经转了，但是relative关系还没有修改，注意这里只是修改了rooty相对于rootx的关系，而对于rooty的所有子节点相对于rootx的关系是没有修改的，这个修改时在find()函数中做的。那么怎么对rooty的relative关系进行修改呢？

animal[RootOfY].relative = (animal[NodeX].relative-animal[NodeY].relative-D+3)%3;

向量解释如下：

 

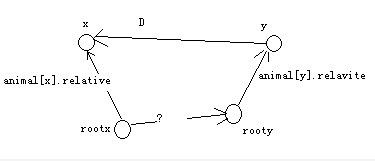
X相对于y的关系已经给了是D，y相对于rooty的关系是animal[y].relative, x相对于rootx的关系是animal[x].relative，那么rooty相对于rootx的关系就是(animal[NodeX].relative-animal[NodeY].relative-D+3)%3;

 

3.

在find（）函数中做的修改： int Find(int NodeToFind) { if(animal[NodeToFind].parent==NodeToFind) return NodeToFind; int temp = animal[NodeToFind].parent; animal[NodeToFind].parent = Find(animal[NodeToFind].parent); animal[NodeToFind].relative = (animal[NodeToFind].relative+animal[temp].relative)%3; return animal[NodeToFind].parent; }  

 

在find函数中除了要返回nodeTofind的根节点，同时还要对在union（）中没有修改的节点的relative关系做修改.

首先用temp存储nodetoFind的父节点，之后递归调用Find()函数，对nodefoFind的父节点的relative做修改，也就是说find()完之后，nodetoFind父节点相对于根节点的关系已经确定了animal[tmp].relative，现在还知道nodetoFind相对于temp节点的关系animal[NodetoFind].relative。

 

于是可以计算nodetofind相对于root的关系：

Animal[nodetofind].relative = (animal[temp].relative + animnal[nodetofind].relative)%3