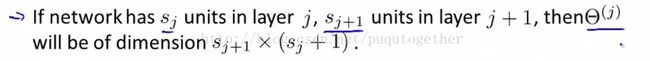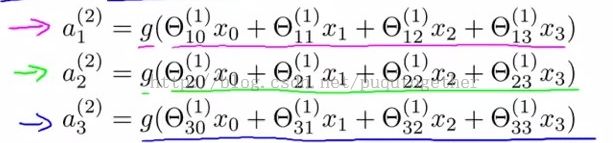Stanford机器学习课程笔记——神经网络的表示
Stanford机器学习课程笔记——神经网络的表示
1. 为什么要引入神经网络
其实这个问题等价与神经网络和之前的回归模型有什么区别,如果你没有学过其他机器学习算法的话。这个问题可以通过一个例子来说明:如果样本都是60*60的图像,那么每个样本的特征维数都是3600个,使用前面讲的线性回归模型,那么需要建立的参数个数就有3600的;如果是非线性回归模型,还要考虑高次项的情况,需要求解的参数就更加多了。此时的回归模型将会变得异常复杂,故我们需要其余比较高效的模型来解决这些实际的问题。这个时候我们就引入了神经网络。
2. 神经网络的表示形式
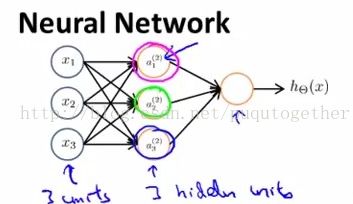
一般而言,神经网络由3部分组成:输入层、中间层和输出层。如下:
其中输入层我们一般用x_1, x_2, x_3,...来表示;中间层我们使用a_j_i来表示第j层的第i个元素。如下:
其中的theta_j(暂且读作theta吧。。。)是第j层到第j+1层的权重矩阵。其矩阵的维数为:
那么中间层的每个元素都可以由输出层x和权重矩阵theta求得。
其实形式就是每个元素都是前面一层的输入和对应的权重相乘再叠加的过程。根据这个思想,我们也可以得到最后输出层的假设,如下:
不知道有没有发现,叠加之后的括号外面还有一个函数嵌套,就是g(),这个前面LR回归中的sigmod函数,也就是说中间层a(2,j)是输入层线性组合的sigmod值,输出又是中间层线性组合的sigmod值。
其实上面那个假设的形式和LR回归还是很接近的,同样的都是每个元素前面乘以对应的系数theta,然后叠加,然后放在sigmod函数中。当时不同的是,和参数相乘的不再是原始特征,而是中间层的最后一层元素,也就是说神经网络不直接使用原始特征来构建假设,而是根据前面中间层的“过滤学习”得到的特征来构建假设。
这里讲到的构建神经网络的顺序都是input->activation->output的顺序,这个是前向传递。
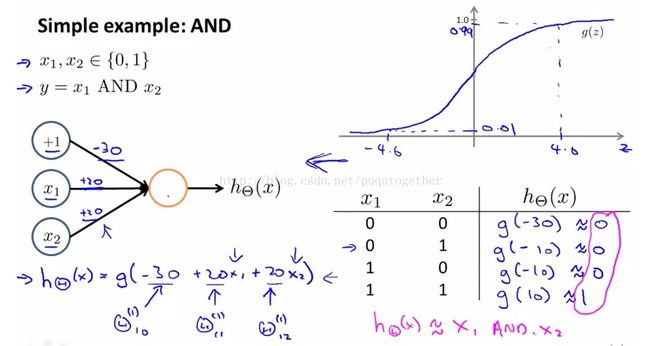
3. 如何用神经网络实现逻辑表示式AND,OR,XNOR
这部分Coursera课程中讲的比较好,画图也丰富,后面给出的Rahcel Zhang的链接也不错,我就直接参考过来吧。。。
逻辑与AND:
逻辑或OR:
我们发现,其实神经网络实现不同的逻辑表达式就是在每一层到下一层的权重矩阵不同而已。说明这个权重矩阵对神经网络的功能至关重要。
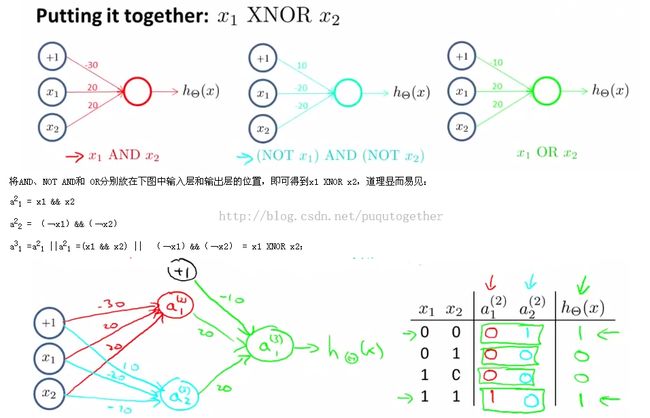
逻辑同或XNOR:
参考:
http://blog.csdn.net/abcjennifer/article/details/7749309
Coursera机器学习笔记