AVL Tree 平衡二叉树基本插入删除节点功能的实现

简述：

实现AVL 树，主要是两个功能 ： 插入某节点和删除某节点

AVL Tree的定义，

1. 是一棵二叉搜索树（故而每个节点是惟一的, 如果出现重复数字会破坏平衡树的算法）

2. 每个节点左右子树的高度之差（平衡因子）相差最多为1

实现：

为了使所得的二叉树为平衡二叉树，

首先在BSTNode中加了一个计算节点高度的方法getHeight()， 当两个节点高度相差2的时候，视为平衡破坏

int getHeight(){
	if(this == NULL)
		return 0;
	if(left == NULL && right == NULL)
		return 1;
	else{
		return 1 + max(left->getHeight(), right->getHeight());
	}
}

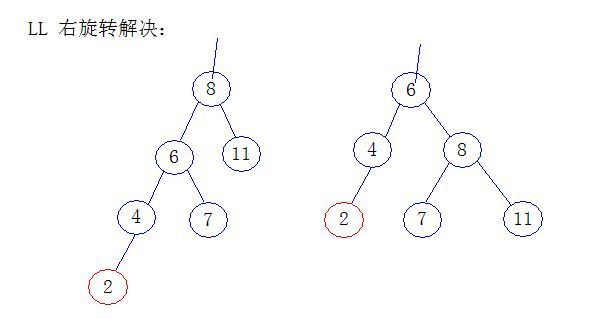
之后讨论一下，不平衡出现的四种情况, 新增节点（红色）

1） LL，  新建在左子树的左节点上

LL代码实现：

template<class Type>
BSTNode<Type>* AVLTree<Type>::LL(BSTNode<Type>* &topNode){
	BSTNode<Type> * leftSonNode = topNode->left;
	topNode->left = leftSonNode->right;
	leftSonNode->right = topNode;
	return leftSonNode;
}

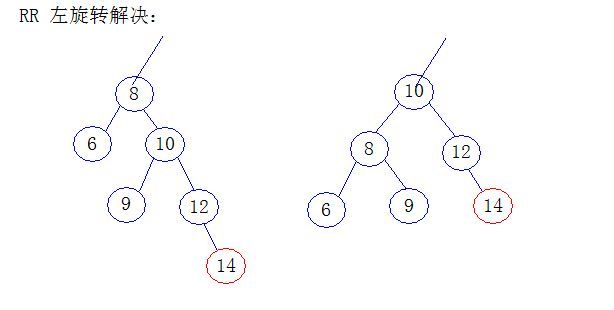
2） RR，  新建在右子树的右节点上

RR代码实现：

template<class Type>
BSTNode<Type>* AVLTree<Type>::RR(BSTNode<Type>* &topNode){
	BSTNode<Type> *rightSonNode = topNode->right;
	topNode->right = rightSonNode->left;
	rightSonNode->left = topNode;
	return rightSonNode;
}

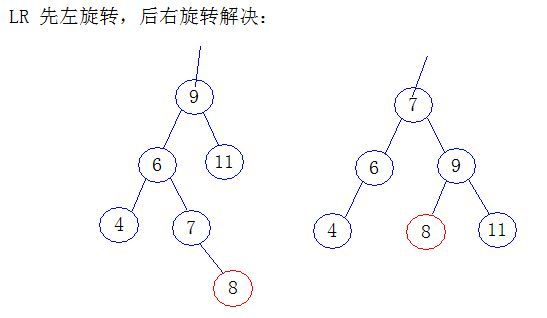
3） LR，  新建在左子树的右节点上

LR代码实现：

template<class Type>
BSTNode<Type>* AVLTree<Type>::LR(BSTNode<Type>* &topNode){
	topNode->left = RR(topNode->left);
	return LL(topNode);
}

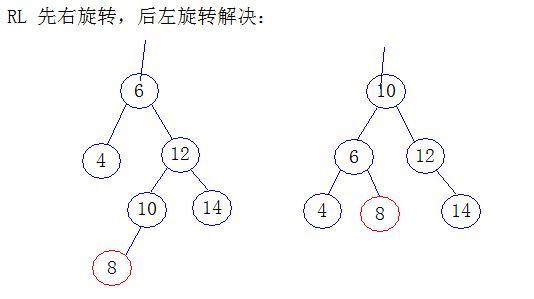
4） RL，  新建在右子树的左节点上

RL代码实现：

template<class Type>
BSTNode<Type>* AVLTree<Type>::RL(BSTNode<Type>* &topNode){
	topNode->right = LL(topNode->right);
	return RR(topNode);
}

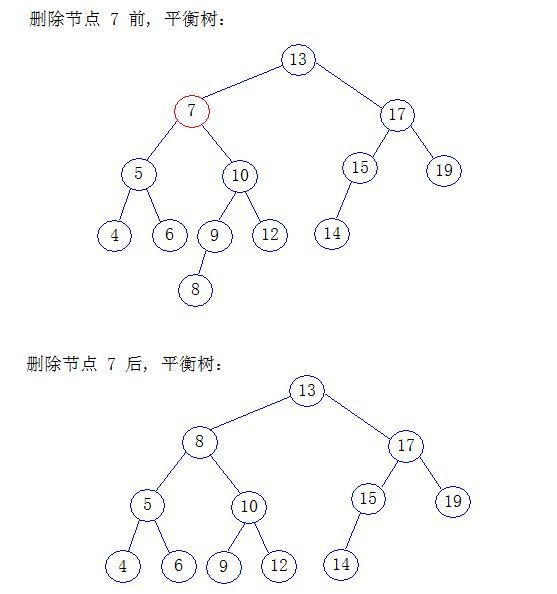
对于删除操作，每一次删除一个节点之后，优先考虑其子节点的最左节点的值替换删除节点，但是需要注意的是，

在替换之后需要自修改节点向下每个节点做Rotate操作，用来处理因为删除某个节点之后平衡树的破坏

下面是Delete函数的实现：

template<class Type>
BSTNode<Type>* AVLTree<Type>::Delete(const Type& key){
	return root = Delete(root, key);
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::Delete(BSTNode<Type>* &node, const Type &key){
	if(node == NULL){
		return NULL;
	}
	/**
	 * if we find the matched key,
	 * delete the matched node and replace it by the most left node
	 * of its right child
	 */
	else if(key == node->key){
		if(!node->right){
			BSTNode<Type> *newNode = node->left;
			delete node;
			return newNode;
		}else{
			BSTNode<Type> *secondMostLeftNode = node->right;
			if(secondMostLeftNode->left == NULL){
				return secondMostLeftNode;
			}
			while(secondMostLeftNode->left->left)
				secondMostLeftNode = secondMostLeftNode->left;
			BSTNode<Type> *mostLeftNode = secondMostLeftNode->left;
			secondMostLeftNode->left->left = node->left;
			secondMostLeftNode->left->right = node->right;
			secondMostLeftNode->left = NULL;
			return mostLeftNode;
		}
	}
	//from bottom to the top
	else if(key < node->key){
		node->left = Delete(node->left, key);
	}
	else{
		node->right = Delete(node->right, key);
	}
	if(node->left)
		node->left = Rotate(node->left);
	if(node->right)
		node->right = Rotate(node->right);
	node = Rotate(node);
	return node;
}


/**
 * Rotate one node and its sub tree
 */
template<class Type>
BSTNode<Type>* AVLTree<Type>::Rotate(BSTNode<Type>* node){
	if(node->left->getHeight() - node->right->getHeight() == 2){
		if(node->left->left->getHeight() >= node->left->right->getHeight())
			node = LL(node);
		else
			node = LR(node);
	}
	if(node->right->getHeight() - node->left->getHeight() == 2){
		if(node->right->right->getHeight() >= node->right->left->getHeight())
			node = RR(node);
		else
			node = RL(node);
	}
	return node;
}

之后是整个平衡树插入删除节点实现以及在main函数中测试的代码：

#include <iostream>
#include <ctime>
#include <cstdlib>
using namespace std;

template<class Type>
class AVLTree;


/**
 * Binary Search Tree Node:  BSTNode class
 */
template<class Type>
class BSTNode{
friend class AVLTree<Type>;
private:
	Type key;
	BSTNode *left;
	BSTNode *right;
public:
	BSTNode(): left(NULL), right(NULL){}
	BSTNode(const Type& key): key(key), left(NULL), right(NULL){}
	Type getkey(){return key;}
	int getHeight(){
		if(this == NULL)
			return 0;
		if(left == NULL && right == NULL)
			return 1;
		else{
			return 1 + max(left->getHeight(), right->getHeight());
		}
	}
	void clear(){
		if(this == NULL)
			return;
		left->clear();
		right->clear();
		delete this;
	}
	void Output_DLR(){ //Node -> left -> Right order
		if(this != NULL){
			cout << key << ", ";
			left->Output_DLR();
			right->Output_DLR();
		}
	}
};


/**
 * AVLTree class
 */
template<class Type>
class AVLTree{
private:
	BSTNode<Type> *root;
public:
	AVLTree(): root(NULL){}
	BSTNode<Type>* Insert(BSTNode<Type>* &, const Type&);
	BSTNode<Type>* Insert(const Type& );
	BSTNode<Type>* Delete(BSTNode<Type>* &, const Type&);
	BSTNode<Type>* Delete(const Type& );
	BSTNode<Type>* Rotate(BSTNode<Type>* );
	BSTNode<Type>* GetRoot();
	BSTNode<Type>* LL(BSTNode<Type>* &);
	BSTNode<Type>* LR(BSTNode<Type>* &);
	BSTNode<Type>* RL(BSTNode<Type>* &);
	BSTNode<Type>* RR(BSTNode<Type>* &);
	void Clear();
	void Output_DLR();
	void Output_LRN();
};


template<class Type>
BSTNode<Type>* AVLTree<Type>::LL(BSTNode<Type>* &topNode){
	BSTNode<Type> * leftSonNode = topNode->left;
	topNode->left = leftSonNode->right;
	leftSonNode->right = topNode;
	return leftSonNode;
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::RR(BSTNode<Type>* &topNode){
	BSTNode<Type> *rightSonNode = topNode->right;
	topNode->right = rightSonNode->left;
	rightSonNode->left = topNode;
	return rightSonNode;
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::LR(BSTNode<Type>* &topNode){
	topNode->left = RR(topNode->left);
	return LL(topNode);
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::RL(BSTNode<Type>* &topNode){
	topNode->right = LL(topNode->right);
	return RR(topNode);
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::GetRoot(){
	return root;
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::Insert(const Type& key){
	return Insert(root, key);
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::Insert(BSTNode<Type>* &node, const Type &key){
	if(node == NULL){
		return node = new BSTNode<Type>(key);
	}
	//from bottom to the top
	else if(key < node->key){
		Insert(node->left, key);
		if(node->left->getHeight() - node->right->getHeight() == 2){
			if(key < node->left->key)
				node = LL(node);
			else
				node = LR(node);
		}
	}
	else{
		Insert(node->right, key);
		if(node->right->getHeight() - node->left->getHeight() == 2){
			if(key > node->right->key)
				node = RR(node);
			else
				node = RL(node);
		}
	}
	return node;
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::Delete(const Type& key){
	return root = Delete(root, key);
}


template<class Type>
BSTNode<Type>* AVLTree<Type>::Delete(BSTNode<Type>* &node, const Type &key){
	if(node == NULL){
		return NULL;
	}
	/**
	 * if we find the matched key,
	 * delete the matched node and replace it by the most left node
	 * of its right child
	 */
	else if(key == node->key){
		if(!node->right){
			BSTNode<Type> *newNode = node->left;
			delete node;
			return newNode;
		}else{
			BSTNode<Type> *secondMostLeftNode = node->right;
			if(secondMostLeftNode->left == NULL){
				return secondMostLeftNode;
			}
			while(secondMostLeftNode->left->left)
				secondMostLeftNode = secondMostLeftNode->left;
			BSTNode<Type> *mostLeftNode = secondMostLeftNode->left;
			secondMostLeftNode->left->left = node->left;
			secondMostLeftNode->left->right = node->right;
			secondMostLeftNode->left = NULL;
			return mostLeftNode;
		}
	}
	//from bottom to the top
	else if(key < node->key){
		node->left = Delete(node->left, key);
	}
	else{
		node->right = Delete(node->right, key);
	}
	if(node->left)
		node->left = Rotate(node->left);
	if(node->right)
		node->right = Rotate(node->right);
	node = Rotate(node);
	return node;
}


/**
 * Rotate one node and its sub tree
 */
template<class Type>
BSTNode<Type>* AVLTree<Type>::Rotate(BSTNode<Type>* node){
	if(node->left->getHeight() - node->right->getHeight() == 2){
		if(node->left->left->getHeight() >= node->left->right->getHeight())
			node = LL(node);
		else
			node = LR(node);
	}
	if(node->right->getHeight() - node->left->getHeight() == 2){
		if(node->right->right->getHeight() >= node->right->left->getHeight())
			node = RR(node);
		else
			node = RL(node);
	}
	return node;
}



template<class Type>
void AVLTree<Type>::Clear(){
	root->clear();
	root = NULL;
}


template<class Type>
void AVLTree<Type>::Output_DLR(){
	if(!root)
		cout << "EMPTY TREE! " << endl;
	else
		root->Output_DLR();
}


template<class Type>
void AVLTree<Type>::Output_LRN(){
	if(!root)
		cout << "EMPTY TREE! " << endl;
	else
		root->Output_LRN();
}

//Test Main
int main() {
	AVLTree<int> *tree = new AVLTree<int>();
	cout << "First, Test Insert(key) funciton: " << endl;
    cout << "Test LL : " << endl;
    //test LL
    tree->Insert(8);
    tree->Insert(6);
    tree->Insert(11);
    tree->Insert(4);
    tree->Insert(7);
    tree->Insert(2);
    cout << "DLR Output LL: " << endl;
    tree->GetRoot()->Output_DLR();
    tree->Clear();

    //test RR
    cout << endl << endl << "Test RR : " << endl;
    tree->Insert(8);
    tree->Insert(6);
    tree->Insert(10);
    tree->Insert(9);
    tree->Insert(12);
    tree->Insert(14);
    cout << "DLR Output RR: " << endl;
    tree->GetRoot()->Output_DLR();
    tree->Clear();

    //test LR
    cout << endl << endl << "Test LR : " << endl;
    tree->Insert(9);
    tree->Insert(6);
    tree->Insert(11);
    tree->Insert(4);
    tree->Insert(7);
    tree->Insert(8);
    cout << "DLR Output LR: " << endl;
    tree->GetRoot()->Output_DLR();
    tree->Clear();


    //test RL
    cout << endl << endl << "Test RL : " << endl;
    tree->Insert(6);
    tree->Insert(4);
    tree->Insert(12);
    tree->Insert(10);
    tree->Insert(14);
    tree->Insert(8);
    cout << "DLR Output RL: " << endl;
    tree->GetRoot()->Output_DLR();
    tree->Clear();

    //test Delete(const Type& )
    cout << endl << endl << "Test Delete : " << endl;
    tree->Insert(6);
    tree->Insert(7);
    tree->Insert(9);
    tree->Insert(13);
    tree->Insert(15);
    tree->Insert(4);
    tree->Insert(5);
    tree->Insert(17);
    tree->Insert(19);
    tree->Insert(12);
    tree->Insert(10);
    tree->Insert(14);
    tree->Insert(8);
    cout << "DLR Output Before Delete: " << endl;
    tree->Output_DLR();
    tree->Delete(7);
    cout << endl << "DLR Output After Delete: " << endl;
    tree->Output_DLR();
    tree->Clear();

	return 0;
}

测试输出：

对于最后的测试Delete的结果，平衡树的改变可以观察下面这副，数据是相同的