支持向量机之序列最小最优化算法

基础博客
线性可分支持向量机
对偶学习算法
线性支持向量机
非线性支持向量机

简介

序列最小最优化（sequential minimal optimization，SMO）算法，是1988年Platt提出的。
论文PDF链接

应用SMO算法要解决的凸二次规划的对偶问题是：

minα12∑Ni=1∑Nj=1αiαjyiyjK(xi,xj)−∑Ni=1
s.t.∑Ni=1αiyi=0
0⩽αi⩽C,i=1,2,...,N

上式中，变量就是拉格朗日乘子 αi ,一个 αi 对应于一个样本点 (xi,yi) ,变量的总数等于训练样本的容量N

基本思想

SMO算法是一种启发式学习算法，基本思路是：如果所有的变量都满足最优化问题的KKT条件，那么这个最优化问题的解可直接得到。因为KKT条件是该最优化问题的充分必要条件。否则，选择两个变量，固定其他变量，针对这两个变量构造一个凸二次规划问题的解。

这个二次规划问题关于这两个变量的解应该是更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。

同时，这时的子问题可以通过解析方法求解，这样可以大大提高整体算法的计算速度。

子问题有两个变量，一个是违反ＫＴＴ田间最严重的那一个，一个是满足ＫＴＴ条件的。

ＳＭＯ算法将原问题不断分解为子问题并对子问题求解，进而达到求原问题的目的。

子问题的两个变量只有一个是自由变量，假设 α1,α2 为两个变量， α2,α3,...,αN 固定，那么约束条件可变为：

α1=−y1∑Ni=2αiyi

如果 α2 确定，那么 α1 也确定，所以子问题同时更像两个变量。

SMO算法包括两个部分：求解两个变量二次规划的解析方法和选择变量的启发式学习方法

两个变量二次规划的求解方法

假设选择的两个变量是 α1,α2 ,其他变量 αi（i=3,4,...,N） 是固定的，于是SMO的最优化问题的子问题可以写成：

minα1,α2W(α1,α2)=12K11α21+12K22α22+y1y2K12α1α2−(α1+α2)+y1α1∑Ni=3yiαiKi1+y2α2∑Ni=3yiαiKi2


s.t. α1y1+α2y2=−∑Ni=3yiαi=ζ
0≤αi≤Ci=1,2

其中： Kij=K(xi,xj),i,j=1,2,..N,ζ 是常数，上面的目标函数中省略了不含有 α1,α2 的常数项

如何求解
先分析约束条件，然后在此约束条件下求极小值
由于只有两个变量 (α1,α2) ,约束可以在二维空间中表示如下图：

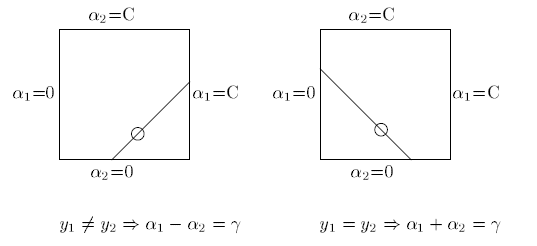
不等式约束使得 (α1,α2) 在盒子 [0,C]x[0,C] 内，等式约束使得 (α1,α2) 在平行于盒子 [0,C]x[0,C] 对角线的直线上。因此要求的是目标函数在一条平行于对角线上的最优值，这使得两个变量的最优化问题成为实质上的单变量的最优化问题，不妨考虑变量 α2 的最优化问题

假设上面问题的初始可行解为 αold1,αold2 ，最优解为 αnew1,αnew2 ，并且假设在沿着约束方向未经剪辑(即：不考虑不等式约束条件)时 α2 的最优解为 αnew,unc2

求满足不等式约束的解
当 αnew2 满足不等式约束 0⩽α2⩽C 时候：
初始可行解为 αold1,αold2 并且满足：
αold1y1+αold2y2=−∑Ni=3yiαi=ζ
0≤αoldi≤Ci=1,2
等式约束两边都乘以 y1
αold1+αold2y2y1=y1ζ=γ

（1）当 y1y2=1 时候约束条件转化为：
αold1+αold2=y1ζ=γ
0≤αold1≤C
0≤αold2≤C

（1.1）当 γ>C 时候：
αnew2 必须在平行于约束盒子对角线的直线上(如Fig1)，可以看出其取值范围是： maxαnew2=C，minαnew2=γ−C
由于 α2在y轴，只需要看直线与两个坐标轴交点的纵坐标就是对于的最大值最小值

（1.2）当 γ<C 时候：
αnew2 必须在平行于约束盒子对角线的直线上(如Fig2)，可以看出其取值范围是： maxαnew2=γ，minαnew2=0

（2）当 y1y2=−1 时候约束条件转化为：
αold1−αold2=y1ζ=γ
0≤αold1≤C
0≤αold2≤C

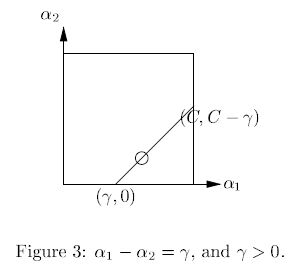
（2.1）当 γ>0 时候：
αnew2 必须在平行于约束盒子对角线的直线上(如Fig3)，可以看出其取值范围是： maxαnew2=C−γ，minαnew2=0

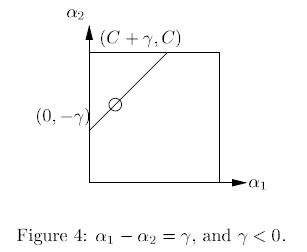
（2.2）当 γ<0 时候：
αnew2 必须在平行于约束盒子对角线的直线上(如Fig4)，可以看出其取值范围是： maxαnew2=−γ，minαnew2=C

根据上面分析，可以求出 αnew2 的取值范围，两个最大值取最小值，两个最小值取最大值
L⩽αnew2⩽H
（1）当 y1y2=1 时
L=max(0,αold2+αold1+C)
H=min(C,αold2+αold1)
注意：这里没有出现 γ 是由于 αold1+αold2=y1ζ=γ 在上面是没消去 γ
(2)当 y1y2=−1 时
L=max(0,αold2−αold1)
H=min(C,C+αold2−αold1)

求不满足不等式约束的解
首先求沿着约束方向不考虑不等式约束时 α2 的最优解 αnew,unc2 ;然后再求满足不等式约束后 α2 的解 αnew2 .
记：

g(x)=∑Ni=1αiyiK(xi,x)+b

令：

Ei=g(xi)−yi=(∑Nj=1αjyjK(xj,xi)+b)−yi，i=1,2

当 i=1,2 时， Ei 为函数 g(x) 对输入 xi 的预测值和真实值输出 yi 之差

引进记号:
vi=∑Nj=3αjyjK(xi,xj)=g(xi)−∑Nj=1αjyjK(xi,xj)−b，i=1,2
原始目标函数是：
minα1,α2W(α1,α2)=12K11α21+12K22α22+y1y2K12α1α2−(α1+α2)+y1α1∑Ni=3yiαiKi1+y2α2∑Ni=3yiαiKi2

可以改写为：
W(α1,α2)=12K11α21+12K22α22+y1y2K12α1α2−(α1+α2)+y1v1α1+y2v2α2

由 α1y1=ζ−α2y2及y2i=1 ，可以将 α1 表示为： α1=(ζ−y2α2)y1 带入上面目标函数，得到只含有 α2 的函数的目标函数:

W(α2)=12K11(ζ−α2y2)2+12K22α22+y2K12(ζ−α2y2)α2−(ζ−α2y2)y1−α2+v1(ζ−α2y2)+y2v2α2

对 α2 求导
∂W∂α2=K11α2+K22α2−2K12α2−K11ζy2+K12ζy2+y1y2−1−v1y2+y2v2

令其为0，得到：
(K11+K22−2K12)α2=y2(y2−y1+ζK11−ζK12+v1−v2)=y2[y2−y1+ζK11−ζK12+(g(x1)−∑2j=1yjαjK1j−b)−(g(x2)−∑2j=1yjαjK2j−b)]

将 ζ=αold1y1+αold2y2 带入，得到：
K11+K22−2K12αnew,nec2=y2((K11+K22−2K12)αold2y2+y2−y1+g(x1)−g(x2))=(K11+K22−2K12)αold2+y2(E1−E2)

将 η=K11+K22−2K12 代入，于是得到：
αnew,unc2=αold2+y2(E1−E2)η

要是 αnew,unc2 满足不等式约束其值必须在 L，H 范围内，从而 αnew2 的值为：

有 αnew2 求得 αnew1
由于 α1y1+α2y2=ζ
则： αold1y1+αold2y2=ζ
αnew1y1+αnew2y2=ζ

αnew1=αold1+y1y2(αold2−αnew2)

于是得到最优问题的解。

变量的选择方法

第1个变量的选择

SMO称选择第1个变量的过程为外层循环。外层循环在训练样本中选取违反KKT条件最严重的样本点，并将其对应的变量作为第1个变量。
也就是，检测 (xi,yi) 是否满足KKT条件，即：
αi=0⇔yig(xi)=1
0≤αi≤C⇔yig(x1)=1
αi=C⇔yig(xi)=1
其中：
g(xi)=∑Nj=1αiyjK(xi,xj)+b

该检验是在误差范围内进行的，在检测中，外层循环首先遍历所有满足条件0<αi