【USACO3.1.4】形成的区域 二维线段树/离散化/矩形切割/浮漂法 【线段树方法以后写】

方法1：浮漂法。

题目意思是，后来的覆盖在前面的上面。

我们可以倒过来， 从后往前。 这样后来的在上面，前面的，从下往上“浮“。

要点1： 2个矩形如何判断不相交？

     一个矩形的最右边，在另外一个矩形最左边。  上下同理。   （程序实现的时候，因为不知道左右上下关系，所以要4个or来判断）

要点2：如何切割：

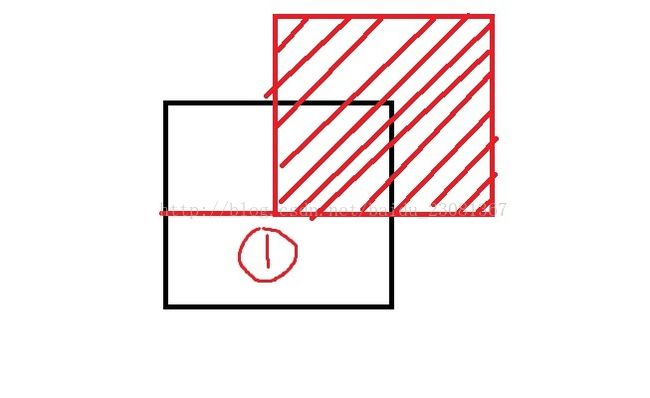
红色的在上面，白色的想上浮。 可以先让1的部分上浮。  上浮后， 矩形变小。（把上浮的地方切掉）

切割后，只有黑色的矩形这一块， 然后再让2的地方上浮。

要点3： 如何知道要切割的地方？

   根据2个矩形的最左边，最右边的坐标关系。  如果【上面】的矩形，的最下面的y1坐标，在【下面】的矩形最上面的y2坐标的”下面“（y1<y2） 那么这一块就要切割（最好画图画一下）

Executing...
   Test 1: TEST OK [0.008 secs, 3424 KB]
   Test 2: TEST OK [0.011 secs, 3424 KB]
   Test 3: TEST OK [0.008 secs, 3424 KB]
   Test 4: TEST OK [0.005 secs, 3424 KB]
   Test 5: TEST OK [0.008 secs, 3424 KB]
   Test 6: TEST OK [0.008 secs, 3424 KB]
   Test 7: TEST OK [0.005 secs, 3424 KB]
   Test 8: TEST OK [0.003 secs, 3424 KB]
   Test 9: TEST OK [0.003 secs, 3424 KB]
   Test 10: TEST OK [0.003 secs, 3424 KB]
   Test 11: TEST OK [0.011 secs, 3424 KB]

All tests OK.

/*
TASK:rect1
LANG:C++
*/
#include <iostream>
#include <cstdio>
using namespace std;

int colo[2510]={1, 0};
int zx[2510]={0},zy[2510]={0},yx[2510],yy[2510];
int output[2510]={0};
int n;

void init()
{
	int ax, ay;
	scanf("%d%d%d", &yx[0], &yy[0], &n);
	for (int i = 1; i <= n; ++ i)	scanf("%d%d%d%d%d", &zx[i], &zy[i], &yx[i], &yy[i], &colo[i]);
}


void cover(int x1, int y1, int x2, int y2, int yanse, int deep)
{
	if (x1 >= x2 || y1 >= y2)	return;//矩形面积为0， 显然直接退出不用做任何计算 
	while (deep <= n && (yx[deep] <= x1 || x2 <= zx[deep] || y2 <= zy[deep] || yy[deep]<= y1)) ++ deep;
	//浮到第deep层，和第deep层的矩形进行比较，看是否有重叠地方。
	//2个矩形如果没有重叠，那么情况一定是
	// 一个矩形最右边，在另外一个矩形最左边的左边。  上下关系同理。 
	// 因为本身不知道2个矩形上下左右关系，所以分4个情况考虑，满足任何一个，就说明2个矩形没有重叠。
	// 如果浮到超过deep层，就结束了
	if (deep > n) //没有覆盖的
	{
		output[yanse] += (x2 - x1)*(y2 - y1);//当前颜色 += 当前面积
		return; 
	}

	if (x1 <= zx[deep])  //分情况分割
	{
		cover(x1, y1, zx[deep], y2, yanse, deep + 1);
		x1 = zx[deep];
	}
	if (yx[deep] <= x2)
	{
		cover(yx[deep], y1, x2, y2, yanse, deep + 1 );
		x2 = yx[deep];
	}
	if (y1 <= zy[deep])
	{
		cover(x1, y1, x2, zy[deep], yanse, deep + 1);
		y1 = zy[deep];
	}	
	if (yy[deep] <= y2)
	{
		cover(x1, yy[deep], x2, y2, yanse, deep + 1);	
		y2 = yy[deep];
	}
}

void doit()
{
	for (int i = n; i >= 0; -- i)
		cover(zx[i],zy[i],yx[i],yy[i], colo[i],i + 1);	
	for (int i = 1; i <= 2500; ++ i)
		if (output[i])	printf("%d %d\n",i, output[i]);
}
int main()
{
	freopen("rect1.in","r",stdin);
	freopen("rect1.out","w",stdout);
	init();
	doit();
	return 0;
}