LCA问题

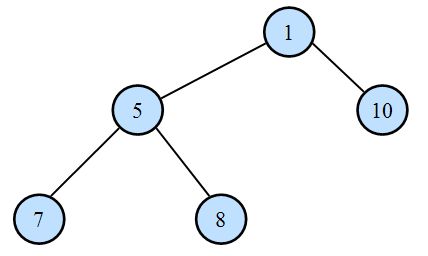
LCA(Least Common Ancestors)问题是指给定一棵树T和两个节点u和v，找出u和v的离根节点最远的公共祖先。 比如说对于下面这棵树，7和10的最近公共祖先是1，7和8的最近公共祖先是5。

可以先想到一个简单的解法。将一个人的祖先全都标记出来，然后顺着另一个的父亲一直向上找，直到找到第一个被标记过的结点，便是它们的最近公共祖先结点了。

#include<map>
#include<set>
#include<iostream>
using namespace std;
int n,m;
string father,son;
set<string> ancestors;
map<string,string> fathers;

int main()
{
	cin>>n;
    for(int i=0;i<n;i++)
	{
        cin>>father>>son;
 		fathers[son]=father;
    }
    cin>>m;
    for(int i=0;i<m;i++)
	{
		string name1,name2;
		cin>>name1>>name2;
        ancestors.clear();
        //把包括name1的所有祖先放到set中 
        while(fathers.count(name1))
		{
            ancestors.insert(name1);
            name1=fathers[name1];
        }
        ancestors.insert(name1);
        //如果name2是name1的祖先直接输出name2 
        if(ancestors.find(name2)!=ancestors.end())
		{
            cout<<name2<<endl;
            continue;
        }
        bool judge=false;
        //否则顺着name2的父亲一直向上找 
        while(fathers.count(name2))
		{
            name2=fathers[name2];
            if(ancestors.find(name2)!=ancestors.end())
			{
                cout<<name2<<endl;
                judge=true;
                break;
            }
        }
        //没有公共祖先输出-1 
        if(!judge) cout<<"-1\n";
    }
}

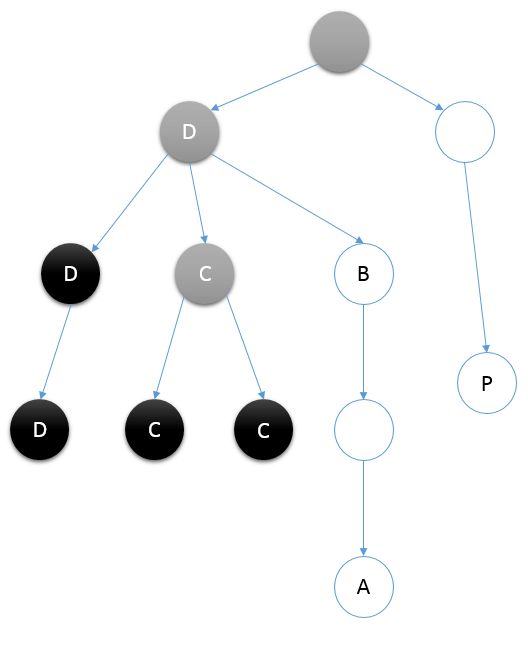
当然这样是非常低效的，在讲解更高效的算法之前我们需要了解一下在线算法和离线算法的概念。一个在线算法是指它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入。相对的，对于一个离线算法，在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。因为在线算法并不知道整个的输入，所以它被迫做出的选择最后可能会被证明不是最优的，对在线算法的研究主要集中在当前环境下怎么做出选择。对于LCA问题，我们分别讨论在线算法和离线算法。先来讲解LCA离线算法。考虑下图的情况。

 

现在以深度优先搜索的顺序来访问这棵树，在这个过程中给这棵树的结点染色，一开始所有结点都是白色的。第一次经过某个结点的时候，将它染成灰色；第二次经过这个结点的时候——也就是离开这棵子树的时候，将它染成黑色。举个例子，当深度优先搜索到A结点时，发现A结点和B结点是我们需要处理的一组询问。这个时候，这个图的染色情况如下图所示。B结点的颜色为灰色，说明进入了以B结点为根的子树，但是还没有从这棵子树中出去。这意味着A结点在B结点所在的子树中，那么B结点就是A和B结点的最近公共祖先了。如果询问的是A和C这两个结点，那么在访问到A的时候，C的颜色是黑色的，这时候最近公共祖先就是C结点向上的第一个灰色结点。

如果询问的是A和P这两个结点，此时P还是白色的，反正深度优先搜索会处理到P结点，那个时候A结点肯定已经不是白色了，所以可以沿用之前的方法进行解决。

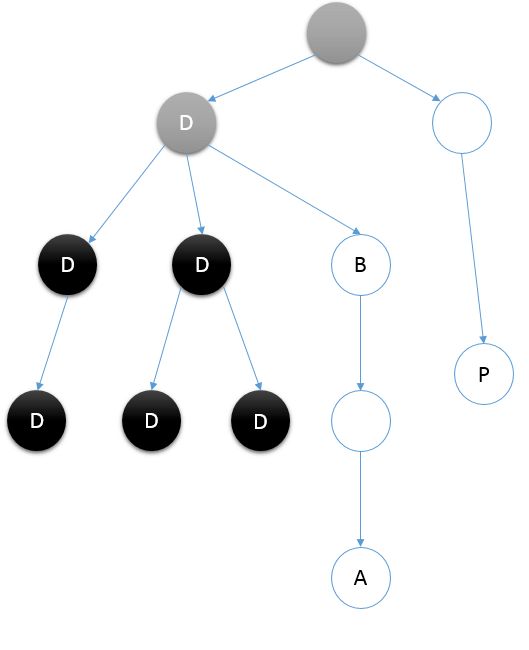
总结一下：计算每个结点涉及到的询问，然后在深度优先搜索的过程中对结点染色，如果发现当前访问的结点是涉及到某个询问，那么就看这个询问中另一个结点的颜色，如果是白色，则留待之后处理；如果是灰色，那么最近公共祖先必然就是这个灰色结点；如果是黑色，那么最近公共祖先就是这个黑色结点向上的第一个灰色结点。唯一剩下的问题，就是怎么样快速的找到一个黑色结点向上的第一个灰色结点。我们来这样想，当深度优先搜索进行到刚刚第二次经过C结点这一步的时候，以C为根的子树中所有结点，它们向上找的第一个灰色结点都是C结点。

如果我们将C这棵子树视为一个集合，而将C结点视为这个集合的代表元素的话，在第二次经过C结点将C结点染成黑色后，以C为根的子树中的所有结点的代表元素都变成了C的父亲结点D结点。这一过程，其实就是将C结点代表的集合合并到了D结点代表的集合中。

每个结点最开始都是一个独立的集合，每当一个结点由灰转黑的时候，就将它所在的集合合并到其父亲结点所在的集合中去。这样无论什么时候，任意一个黑色结点所在集合的代表元素就是这个结点向上的第一个灰色结点。之所以可以这样做是因为这样的染色是不可逆的，对于一个黑色结点来说，它向上找的第一个灰色结点只会越来越高，这和集合的性质是相似的。

#include<map>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int pre[MAXN],cnt=0;
const int MAXN=100010;
map<string,int>map1;
vector<int>g[MAXN];
vector<int>query[MAXN];
string q1[MAXN],q2[MAXN],ans[MAXN],names[MAXN];

int init(string &str)
{
	if(map1[str]==0)
	{
		map1[str]=++cnt;
		names[cnt]=str;
    }
    return map1[str];
}

int find(int x)        
{   
    int r=x;  
    while(pre[r]!=r) r=pre[r];    
    int i=x,j;     
    while(i!=r)                                          
    {  
         j=pre[i];   
         pre[i]=r;   
         i=j;  
    }  
    return r;  
}  

void lca(int u,int v)
{
    pre[u]=u;
    for(int i=0;i<g[u].size();i++) lca(g[u][i],u);
    //深度优先搜索 
    for(int i=0;i<query[u].size();i++)
    {
        int j=query[u][i];
        int k=map1[q1[j]]==u?map1[q2[j]]:map1[q1[j]];
        //j和k表示一组询问 
        if(pre[k]==-1) continue;
    	//如果另外一个点还没访问过就先不处理 
        ans[j]=names[find(k)]; 
    }
    //合并集合 
    pre[u]=find(v);
}

int main()
{
    int n,m;
    string name1,name2 ;
    cin>>n;
    while(n--)
    {
        cin>>name1>>name2;
        int a=init(name1);
        int b=init(name2);
        //把字符串转化为从1开始的数字方便处理 
        g[a].push_back(b);
    }
    cin>>m;
    for(int i=0;i<m;i++)
    {
		cin>>q1[i]>>q2[i];
        query[map1[q1[i]]].push_back(i);
        query[map1[q2[i]]].push_back(i);
    }
    memset(pre,-1,sizeof(pre));     
    pre[0]=0;
    //把0设置为根节点 
    lca(1,0);
    for(int i=0;i<m;i++) cout<<ans[i]<<endl;
}

再来讲解LCA在线算法。从树的根节点开始进行深度优先搜索，每次经过某一个点，无论是从它的父亲节点进入这个点，还是从它的儿子节点返回这个点，都按顺序记录下来。这样，就把一棵树转换成了一个数组。而找到树上两个节点的最近公共祖先，无非就是找到这两个节点最后一次出现在数组中的位置所囊括的一段区间中深度最小的那个点，这样我们就把这个问题转化为了RMQ问题。按照我的理解第几次都不会错，因为无论是第几次那段区间都构成了一条连通的路径，一定会经过最近公共祖先。只不过一般都是选的第一次或者最后一次而已，这样区间会短一些。

#include<cmath> 
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 100000
#define max_name_length 30
#define hash_table_size 100003
using namespace std;
char names[2*MAXN][max_name_length];
int smallest[2*MAXN][17],last_appear[2*MAXN],record_count=0;
int height_of_name[2*MAXN],spring_head[2*MAXN],spring_next[2*MAXN],name_count=0;
int hash_table[hash_table_size],hash_nodes[2*MAXN+1],hash_next[2*MAXN+1],hash_node_count=0;

//返回最小的高度 
int min(int a,int b) 
{
	return (height_of_name[a]<=height_of_name[b])?a:b;
}

//采用BKDR算法计算hash值 
unsigned int BKDRHash(char *str) 
{
    unsigned int seed=131; 
	//seed可以取31 131 1313 13131 131313等 
    unsigned int hash=0;
    while(*str) hash=hash*seed+(*str++);
    return hash;
}

//建立hash表 
int myhash(char *str) 
{
    int hash_code,current_node;
    hash_code=BKDRHash(str)%hash_table_size;
    current_node=hash_table[hash_code];
    if(!current_node) 
	{
        hash_table[hash_code]=++hash_node_count;
        return (hash_nodes[hash_node_count]=name_count++);
    }
    while(strcmp(names[hash_nodes[current_node]],str)) 
	{
        if(!hash_next[current_node]) 
		{
            hash_next[current_node]=++hash_node_count;
            return(hash_nodes[hash_node_count]=name_count++);
        }
        current_node=hash_next[current_node];
    }
    return hash_nodes[current_node];
}

//加入记录 
void add_record(int new_record)
{
    smallest[record_count][0]=new_record;
	last_appear[new_record]=record_count++;
}

//dfs遍历 
void travel(int now,int height) 
{
    int spring;
    height_of_name[now]=height;
    add_record(now);
	for(spring=spring_head[now];spring;spring=spring_next[spring]) 
	{
        travel(spring,height+1);
        add_record(now);
    }
} 

//预处理得到2次幂区间的最小值 
void get_smallest() 
{
    int level,length,half_length,i,j,end;
    level=(int)((log(record_count))/(log(2.0)));
    for(i=1;i<=level;++i) 
	{
        length=(1<<i);
        half_length=(length>>1);
		end=record_count+1-length;
        for(j=0;j<end;++j) smallest[j][i]=min(smallest[j][i-1],smallest[j+half_length][i-1]);
    }
}

//处理每段查询 
int query_smallest(int index1,int index2)
{
    int level,length,l,r;
    index1=last_appear[index1];
    index2=last_appear[index2];
    if(index1<=index2) 
	{
        l=index1;
        r=index2;
    }
	else 
	{
        l=index2;
        r=index1;
    }
    level=(int)((log(r+1-l))/(log(2.0)));
    length=(1<<level);
    return min(smallest[l][level],smallest[r+1-length][level]);
}

int main()
{
    int n_relation,n_request,father_index,son_index,index1,index2;
    char name1[max_name_length],name2[max_name_length];
    scanf("%d",&n_relation);
    memset(spring_head,0,n_relation *2*sizeof(int));
    memset(hash_table,0,hash_table_size*sizeof(int));
    memset(hash_next+1,0,n_relation*2*sizeof(int));
    while(n_relation--)
	{
        scanf("%s",names[name_count]);
        father_index=myhash(names[name_count]);
        scanf("%s",names[name_count]);
        son_index=myhash(names[name_count]);
        //建立链表 
        spring_next[son_index]=spring_head[father_index];
        spring_head[father_index]=son_index;
    }
    travel(0,0);
    get_smallest();
    scanf("%d",&n_request);
    for(int i=0;i<n_request;++i) 
	{
        scanf("%s%s",name1,name2);
        index1=myhash(name1);
        index2=myhash(name2);
        puts(names[query_smallest(index1,index2)]);
    }
}