CNN 卷积神经网络-- 残差计算
前言
本文主要是解析论文Notes onConvolutional Neural Networks的公式,参考了http://blog.csdn.net/lu597203933/article/details/46575871的公式推导,借用https://github.com/BigPeng/JavaCNN代码
CNN
cnn每一层会输出多个feature map, 每个feature map由多个神经元组成,假如某个feature map的shape是m*n, 则该feature map有m*n个神经元
卷积层
卷积计算
设当前层l为卷积层,下一层l+1为子采样层subsampling.
则卷积层l的输出feature map为:
Xlj=f(∑i∈MjXl−1i∗klij+blj)
∗ 为卷积符号
残差计算
设当前层l为卷积层,下一层l+1为子采样层subsampling.
第l层的第j个feature map的残差公式为:
δlj=βl+1j(f′(μlj)∘up(δl+1j))(1)
其中
f(x)=11+e−x(2) ,
其导数
f′(x)=f(x)∗(1−f(x))(3)
为了之后的推导,先提前讲讲subsample过程,比较简单,假设采样层是对卷积层的均值处理,如卷积层的输出feature map( f(μlj) )是
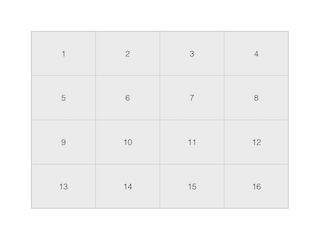
则经过subsample的结果是:

subsample过程如下:
import java.util.Arrays;
/** * Created by keliz on 7/7/16. */
public class test {
/** * 卷积核或者采样层scale的大小,长与宽可以不等. */
public static class Size {
public final int x;
public final int y;
public Size(int x, int y)
{
this.x = x;
this.y = y;
}
}
/** * 对矩阵进行均值缩小 * * @param matrix * @param scale * @return */
public static double[][] scaleMatrix(final double[][] matrix, final Size scale)
{
int m = matrix.length;
int n = matrix[0].length;
final int sm = m / scale.x;
final int sn = n / scale.y;
final double[][] outMatrix = new double[sm][sn];
if (sm * scale.x != m || sn * scale.y != n)
throw new RuntimeException("scale不能整除matrix");
final int size = scale.x * scale.y;
for (int i = 0; i < sm; i++)
{
for (int j = 0; j < sn; j++)
{
double sum = 0.0;
for (int si = i * scale.x; si < (i + 1) * scale.x; si++)
{
for (int sj = j * scale.y; sj < (j + 1) * scale.y; sj++)
{
sum += matrix[si][sj];
}
}
outMatrix[i][j] = sum / size;
}
}
return outMatrix;
}
public static void main(String args[])
{
int row = 4;
int column = 4;
int k = 0;
double[][] matrix = new double[row][column];
Size s = new Size(2, 2);
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j)
matrix[i][j] = ++k;
double[][] result = scaleMatrix(matrix, s);
System.out.println(Arrays.deepToString(matrix).replaceAll("],", "]," + System.getProperty("line.separator")));
System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
}
}
其中3.5=(1+2+5+6)/(2*2); 5.5=(3+4+7+8)/(2*2)
由此可知,卷积层输出的feature map中的值为1的节点,值为2的节点,值为5的节点,值为6的节点(神经元)与subsample层的值为3.5的节点相连接,值为3,值为4,值为7,值为8节点与subsample层的值为5.5节点相连接。由BP算法章节的推导结论可知
卷积层第j个节点的残差等于子采样层与其相连接的所有节点的权值乘以相应的残差的加权和再乘以该节点的导数
对着公式看比较容易理解这句话。
假设子采样层的对应文中的卷积层的残差 δl+1j 是,

按照公式(1),节点1值为0.5的残差是
因为这是计算单个神经元的残差,所以需要把 ∘ 换成 ∗ , ∘ 这个运算符代表矩阵的点乘即对应元素相乘,而且 节点(神经元)1的对应子采样层的值为3.5的节点, 由 公式(3),可知节点1的残差是
即
同理,对于节点2,
残差为
对于节点5,
残差为
对于节点6,
残差为
因为节点3对应的子采样层的残差是0.6,所以节点3的残差为
即
公式(1)使用了一个技巧,实现这个计算过程,把子采样层的残差 δl+1j 与一个全一矩阵(shape与 δl+1j 一样)做克罗内克积,
即

与
做克罗内克积 .
结果是
计算过程:
import java.util.Arrays;
/** * Created by keliz on 7/7/16. */
public class kronecker {
/** * 卷积核或者采样层scale的大小,长与宽可以不等. */
public static class Size {
public final int x;
public final int y;
public Size(int x, int y)
{
this.x = x;
this.y = y;
}
}
/** * 克罗内克积,对矩阵进行扩展 * * @param matrix * @param scale * @return */
public static double[][] kronecker(final double[][] matrix, final Size scale) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m * scale.x][n * scale.y];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int ki = i * scale.x; ki < (i + 1) * scale.x; ki++) {
for (int kj = j * scale.y; kj < (j + 1) * scale.y; kj++) {
outMatrix[ki][kj] = matrix[i][j];
}
}
}
}
return outMatrix;
}
public static void main(String args[])
{
int row = 2;
int column = 2;
double k = 0.5;
double[][] matrix = new double[row][column];
Size s = new Size(2, 2);
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j){
matrix[i][j] = k;
k += 0.1;
}
System.out.println(Arrays.deepToString(matrix).replaceAll("],", "]," + System.getProperty("line.separator")));
double[][] result = kronecker(matrix, s);
System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
}
}将 f′(μlj) 矩阵与这个克罗内克积的结果矩阵做点乘再乘以 βl+1j ,就可以得到该卷积层的残差.
子采样层
采样计算
假设采样层是对卷积层的均值处理,如卷积层的输出feature map( f(μlj) )是

则经过subsample的结果是:

公式为:
Xlj=f(βljdown(Xl−1j)+blj)
down(Xl−1j) 对 Xl−1j 中的2*2大小中的像素值求和。
卷积与子采样层的计算公式都包含 β 与 b 参数,但是本文默认不处理.
subsample过程如下:
import java.util.Arrays;
/** * Created by keliz on 7/7/16. */
public class test {
/** * 卷积核或者采样层scale的大小,长与宽可以不等. */
public static class Size {
public final int x;
public final int y;
public Size(int x, int y)
{
this.x = x;
this.y = y;
}
}
/** * 对矩阵进行均值缩小 * * @param matrix * @param scale * @return */
public static double[][] scaleMatrix(final double[][] matrix, final Size scale)
{
int m = matrix.length;
int n = matrix[0].length;
final int sm = m / scale.x;
final int sn = n / scale.y;
final double[][] outMatrix = new double[sm][sn];
if (sm * scale.x != m || sn * scale.y != n)
throw new RuntimeException("scale不能整除matrix");
final int size = scale.x * scale.y;
for (int i = 0; i < sm; i++)
{
for (int j = 0; j < sn; j++)
{
double sum = 0.0;
for (int si = i * scale.x; si < (i + 1) * scale.x; si++)
{
for (int sj = j * scale.y; sj < (j + 1) * scale.y; sj++)
{
sum += matrix[si][sj];
}
}
outMatrix[i][j] = sum / size;
}
}
return outMatrix;
}
public static void main(String args[])
{
int row = 4;
int column = 4;
int k = 0;
double[][] matrix = new double[row][column];
Size s = new Size(2, 2);
for (int i = 0; i < row; ++i)
for (int j = 0; j < column; ++j)
matrix[i][j] = ++k;
double[][] result = scaleMatrix(matrix, s);
System.out.println(Arrays.deepToString(matrix).replaceAll("],", "]," + System.getProperty("line.separator")));
System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
}
}
其中3.5=(1+2+5+6)/(2*2); 5.5=(3+4+7+8)/(2*2)
残差计算
设当前层l为子采样层,下一层l+1为卷积层.
第l层的第j个feature map的残差公式为:
δlj=f′(μlj)∘conv2(δl+1j,rot180(kl+1j),full)(5)
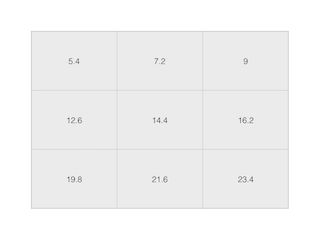
设子采样层的输出feature map( f(μlj) )是

对应的卷积层的kernel( kl+1j )为

则卷积层输出的feature map为
假设卷积层的delta( δl+1j )为
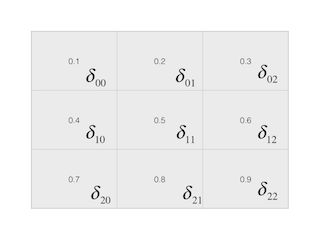
delta与feature map是一一对应
计算过程:
import java.util.Arrays;
/** * Created by keliz on 7/7/16. */
public class conv {
/** * 复制矩阵 * * @param matrix * @return */
public static double[][] cloneMatrix(final double[][] matrix) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
outMatrix[i][j] = matrix[i][j];
}
}
return outMatrix;
}
/** * 对矩阵进行180度旋转,是在matrix的副本上复制,不会对原来的矩阵进行修改 * * @param matrix */
public static double[][] rot180(double[][] matrix) {
matrix = cloneMatrix(matrix);
int m = matrix.length;
int n = matrix[0].length;
// 按列对称进行交换
for (int i = 0; i < m; i++) {
for (int j = 0; j < n / 2; j++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
// 按行对称进行交换
for (int j = 0; j < n; j++) {
for (int i = 0; i < m / 2; i++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[m - 1 - i][j];
matrix[m - 1 - i][j] = tmp;
}
}
return matrix;
}
/** * 计算valid模式的卷积 * * @param matrix * @param kernel * @return */
public static double[][] convnValid(final double[][] matrix,
double[][] kernel) {
kernel = rot180(kernel);
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
// 需要做卷积的列数
int kns = n - kn + 1;
// 需要做卷积的行数
final int kms = m - km + 1;
// 结果矩阵
final double[][] outMatrix = new double[kms][kns];
for (int i = 0; i < kms; i++) {
for (int j = 0; j < kns; j++) {
double sum = 0.0;
for (int ki = 0; ki < km; ki++) {
for (int kj = 0; kj < kn; kj++)
sum += matrix[i + ki][j + kj] * kernel[ki][kj];
}
outMatrix[i][j] = sum;
}
}
return outMatrix;
}
public static void main(String args[]) {
int subSampleLayerRow = 4;
int subSampleLayerColumn = 4;
int subSampleLayerK = 0;
double[][] subSampleLayer = new double[subSampleLayerRow][subSampleLayerColumn];
for (int i = 0; i < subSampleLayerRow; ++i)
for (int j = 0; j < subSampleLayerColumn; ++j)
subSampleLayer[i][j] = ++subSampleLayerK;
int kernelRow = 2;
int kernelColumn = 2;
double kernelK = 0.3;
double[][] kernelMatrix = new double[kernelRow][kernelColumn];
for (int i = 0; i < kernelRow; ++i)
for (int j = 0; j < kernelColumn; ++j){
kernelMatrix[i][j] = kernelK;
kernelK += 0.1;
}
System.out.println(Arrays.deepToString(kernelMatrix).replaceAll("],", "]," + System.getProperty("line.separator")));
double[][] result = convnValid(subSampleLayer, kernelMatrix);
System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
}
}
注意:卷积计算时,需要对kernel先旋转180度
从计算过程可以看出,卷积层输出的feature map中的神经元(0,0)值为7.2是由子采样层的输出feature map中的(0,0)值为1,(0,1)值为2,(1,0)值为5,(1,1)值为6生成,即子采样层的输出feature map中的(0,0)与卷积层 δ00 相连接,与卷积层 δ 其它节点不相连。
再如,卷积层输出的feature map中的神经元(0,1)值为9.0是由子采样层的输出feature map中的(0,1)值为2,(0,2)值为3,(1,1)值为6,(1,2)值为7生成,则即子采样层的输出feature map中的(0,1)与卷积层 δ01 相连接, 但是从上面的描述克制 δ00 也是由子采样层的输出feature map中的(0,1)生成的,即子采样层的输出feature map中的(0,1)与卷积层 δ00 , δ01 相连接,与卷积层 δ 其它节点不相连。
再如,卷积层输出的feature map中的神经元(1,0)值为14.4是由子采样层的输出feature map中的(1,0)值为5,(1,1)值为6,(2,0)值为9,(2,1)值为10生成。
卷积层输出的feature map中的神经元(1,1)值为16.2是由子采样层的输出feature map中的(1,1)值为6,(1,2)值为7,(2,1)值为10,(2,2)值为11生成.
反过来,从这几部分可以看出,子采样层的输出feature map中的(1,1)值为6, 是与卷积层 δ00 , δ01 , δ10 , δ11 相连接.
由前一章节的BP算法推导结论可知
子采样层第j个节点的残差等于卷积层与其相连接的所有节点的权值乘以相应的残差的加权和再乘以该子采样层节点的导数。
由于子采样层节点(0,0)值为1只与卷积层 δ00 相连接,因此其残差为
δ(0,0)=f′(1)∗kernel(1,1)∗δ00(6)
即
δ(0,0)=f′(1)∗0.6∗0.1(7)
子采样层节点(0,1)值为2与卷积层 δ0,0 , δ01 相连接,因此其残差为
δ(0,1)=f′(2)∗(kernel(1,0)∗δ00+kernel(1,1)∗δ01)(8)
因为卷积层 δ00 是由 δ(0,1)∗kernel(1,0) 与其它节点一起计算出来,同理卷积层 δ01 是由 δ(0,1)∗kernel(1,1) 与其它节点一起计算出来,因此公式8是 kernel(1,0)∗δ00 和 kernel(1,1)∗δ01 ,这个过程,可以手动计算一下就明白。
子采样层节点(1,1)值为6与卷积层 δ0,0 , δ01 , δ10 , δ11 相连接,因此其残差为
δ(1,1)=f′(6)∗(kernel(0,0)∗δ00+kernel(0,1)∗δ01+kernel(1,0)∗δ10+kernel(1,1)∗δ11)(9)
以此类推可以得出子采样层的残差:
δ(0,0)=f′(1)∗kernel(1,1)∗δ00(10)
δ(0,1)=f′(2)∗(kernel(1,0)∗δ00+kernel(1,1)∗δ01)(11)
δ(0,2)=f′(3)∗(kernel(1,0)∗δ01+kernel(1,1)∗δ02)(12)
δ(0,3)=f′(4)∗(kernel(1,0)∗δ02)(13)
δ(1,0)=f′(5)∗(kernel(1,1)∗δ10+kernel(0,1)∗δ00)(14)
δ(1,1)=f′(6)∗(kernel(0,0)∗δ00+kernel(0,1)∗δ01+kernel(1,0)∗δ10+kernel(1,1)∗δ11)(15)
δ(1,2)=f′(7)∗(kernel(0,0)∗δ01+kernel(0,1)∗δ02+kernel(1,0)∗δ11+kernel(1,1)∗δ12)(16)
δ(1,3)=f′(8)∗(kernel(0,0)∗δ02+kernel(1,0)∗δ12)(17)
δ(2,0)=f′(9)∗(kernel(0,1)∗δ10+kernel(1,1)∗δ20)(18)
δ(2,1)=f′(10)∗(kernel(0,0)∗δ10+kernel(0,1)∗δ11+kernel(1,0)∗δ20+kernel(1,1)∗δ21)(19)
δ(2,2)=f′(11)∗(kernel(0,0)∗δ11+kernel(0,1)∗δ12+kernel(1,0)∗δ21+kernel(1,1)∗δ22)(20)
δ(2,3)=f′(12)∗(kernel(0,0)∗δ12+kernel(1,0)∗δ22)(21)
δ(3,0)=f′(13)∗(kernel(0,1)∗δ20)(22)
δ(3,1)=f′(14)∗(kernel(0,0)∗δ20+kernel(0,1)∗δ21)(23)
δ(3,2)=f′(15)∗(kernel(0,0)∗δ21+kernel(0,1)∗δ22)(24)
δ(3,3)=f′(16)∗(kernel(0,0)∗δ22)(25)
这个残差计算过程使用公式(5)描述,这其中跟卷积层的残差计算一样,有一个小技巧,用卷积层的残差矩阵与旋转180度后的卷积层kernel做full 模式的卷积,因为在mathlab中,计算卷积时,需要旋转180度后再进行卷积,而这个残差计算过程是不要旋转的,因此需要事先把它旋转180度。看看下面这个过程,就知道为什么不需要旋转180度。
设 δl+1j 的shape为(dRowSize, dColumSize)
kl+1j 的shape为(kRowSize, kColumSize)
conv的full模式需要把 δl+1j 扩展为shape为((dRowSize + 2 * (kRowSize - 1)), (dColumSize + 2 * (kColumSize - 1))),
即卷积层的delta( δl+1j )

扩展为

此时用旋转180度的kernel,与扩展后的 δl+1j 做卷积在乘以相应的激励值,即可得到子采样层的残差,与公式(10-25)一致
 ,
,
import java.util.Arrays;
/** * Created by keliz on 7/7/16. */
public class convFull {
/** * 计算full模式的卷积 * * @param matrix * @param kernel * @return */
public static double[][] convnFull(double[][] matrix,
final double[][] kernel) {
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
// 扩展矩阵
final double[][] extendMatrix = new double[m + 2 * (km - 1)][n + 2
* (kn - 1)];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++)
extendMatrix[i + km - 1][j + kn - 1] = matrix[i][j];
}
return convnValid(extendMatrix, kernel);
}
/** * 计算valid模式的卷积 * * @param matrix * @param kernel * @return */
public static double[][] convnValid(final double[][] matrix,
double[][] kernel) {
kernel = rot180(kernel);
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
// 需要做卷积的列数
int kns = n - kn + 1;
// 需要做卷积的行数
final int kms = m - km + 1;
// 结果矩阵
final double[][] outMatrix = new double[kms][kns];
for (int i = 0; i < kms; i++) {
for (int j = 0; j < kns; j++) {
double sum = 0.0;
for (int ki = 0; ki < km; ki++) {
for (int kj = 0; kj < kn; kj++)
sum += matrix[i + ki][j + kj] * kernel[ki][kj];
}
outMatrix[i][j] = sum;
}
}
return outMatrix;
}
/** * 复制矩阵 * * @param matrix * @return */
public static double[][] cloneMatrix(final double[][] matrix) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
outMatrix[i][j] = matrix[i][j];
}
}
return outMatrix;
}
/** * 对矩阵进行180度旋转,是在matrix的副本上复制,不会对原来的矩阵进行修改 * * @param matrix */
public static double[][] rot180(double[][] matrix) {
matrix = cloneMatrix(matrix);
int m = matrix.length;
int n = matrix[0].length;
// 按列对称进行交换
for (int i = 0; i < m; i++) {
for (int j = 0; j < n / 2; j++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
// 按行对称进行交换
for (int j = 0; j < n; j++) {
for (int i = 0; i < m / 2; i++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[m - 1 - i][j];
matrix[m - 1 - i][j] = tmp;
}
}
return matrix;
}
public static void main(String args[]) {
int deltaRow = 3;
int deltaColum = 3;
double initDelta = 0.1;
double[][] delta = new double[deltaRow][deltaColum];
for(int i = 0; i < deltaRow; ++i)
for(int j = 0; j < deltaColum; ++j){
delta[i][j] = initDelta;
initDelta += 0.1;
}
int kernelRow = 2;
int kernelColum = 2;
double initKernel = 0.3;
double[][] kernel = new double[kernelRow][kernelColum];
for(int i = 0; i < kernelRow; ++i)
for(int j = 0; j < kernelColum; ++j){
kernel[i][j] = initKernel;
initKernel += 0.1;
}
double[][] result = convnFull(delta, kernel);
System.out.println(Arrays.deepToString(result).replaceAll("],", "]," + System.getProperty("line.separator")));
}
}参考文献
JavaCNN
CNN公式推导
Notes onConvolutional Neural Networks
Notes onConvolutional Neural Networks论文翻译