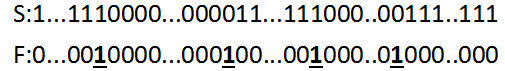JZOJ.4302[NOIP2015模拟11.3]IOIOI卡片占卜 解题报告

IOIOI卡片占卜

题目大意

给5个正整数 A , B , C , D , E 。表示由 A 个1， B 个0， C 个1， D 个0， E 个1连接组成的序列。
接下来给出 n 个操作，每个操作两个整数 l ， r ，表示把 l ~~ r 之间的元素1变成0,0变成1，代价为（ r - l + 1 )。
问将序列全部元素变为1的最小的代价。

输入格式

第一行5个空格分隔的整数 A , B , C , D , E ，意义见题目大意。
接下来一行一个正整数 N ，表示操作种类数。
接下来N行，第i行( 1 ≤ i ≤ N )两个空格分隔的正整数 Li ， Ri 。
表示第i种操作为把 Li ~~ Ri 之间的全部元素由1变成0,由0变成1，代价为（ Ri - Li + 1 )。

输出格式

输出最小代价。如无法实现目标，则输出 −1 .

样例输入

1 2 3 4 5
3
2 3
2 6
4 10

样例输出

12

样例解释

初始的序列为100111000011111。
执行第2种操作后得到111000000011111，代价为5。
接下来执行第3种操作，得到111111111111111，代价为7。
代价为12，这是最小最小代价，故输出12。

数据范围

对于15%的数据，N≤ 10
对于另外50%的数据， 1 ≤ A , B , C , D , E ≤ 50
对于100%的数据：
1 ≤ A , B , C , D , E , N ≤ 105
1 ≤ Li ≤ Ri ≤ A + B + C + D + E ( 1 ≤ i ≤ N )

题解

15分算法

先讲一下15分的算法。
用 2n 的时间复杂度枚举所有的操作选择方案，看一下能否实现目标并统计最小代价即可。

100分算法

设原序列为 S
定义序列 F ， Fi = Si xor Si+1 。

S ， F 序列内所含元素如下：

新的 F 序列变成一堆0夹着4个1，我们的目标也就变成将 F 序列全部变成0。
对于第 i 个操作 Li ， Ri 也就变成了把 F [ Li -1]和 F [ Ri ]由0变成1，由1变成0。

转换完以后，我们可以怎样做呢？
我们把 Li -1向 Ri 连上一条权为 Ri - Li +1的双向边。
对于一条最短路径，路径上的每个点 F 值的变化次数等于入度加上出度，这很明显。
又因为这是最短路径，所以除了起点和终点以外，每个点的入度和出度都为1，既 F 的值没有变化。
然而起点的入度和出度的和为1，所以起点和终点的值会产生变化。

现在只需将这4个1分成两组，每组分别选一个1作为起点和另一个1作为终点，
做两次SPFA求最短路，并把两组的最小代价累加求最大值即可。

至于分组，只有三种情况。
<1>（1，2），（3，4）
<2>（1，3），（2，4）
<3>（1，4），（2，3）

Code(pascal)

const
    zs=3;
    maxn=maxlongint*100;
var
    way:array[1..zs,1..4] of longint=
    ((1,2,3,4),(1,3,2,4),(1,4,2,3));
    a,b,c,d,e,i,j,k,l,o,p,n,m,bs,len:longint;
    zdl,en:array[-1..500000] of int64;
    fa:array[1..4] of longint;
    bz:array[-1..600000] of boolean;
    bj:array[0..600000,1..3] of int64;
    ans:int64;
function min(a,b:int64):int64;
    begin
        if a<b then exit(a)
        else exit(b);
    end;
procedure add(a,b,c:longint);
    begin
        inc(bs);
        bj[bs,1]:=a;
        bj[bs,2]:=b;
        bj[bs,3]:=c;
        inc(en[a]);
    end;
procedure qsort(l,r:longint);
    var
        i,j,m:longint;
    begin
        i:=l;
        j:=r;
        m:=bj[(l+r) div 2,1];
        repeat
            while bj[i,1]<m do inc(i);
            while bj[j,1]>m do dec(j);
            if i<=j then
            begin
                bj[0]:=bj[i];
                bj[i]:=bj[j];
                bj[j]:=bj[0];
                inc(i);
                dec(j);
            end;
        until i>j;
        if l<j then qsort(l,j);
        if i<r then qsort(i,r);
    end;
function js(start,finish:longint):int64;
    var
         i,j,l,k,o,p:longint;
         dl:array[1..500000] of int64;
    begin
        for i:=0 to len do
        begin
            zdl[i]:=maxn;
            bz[i]:=false;
        end;
        zdl[start]:=0;
        j:=1;
        dl[j]:=start;
        i:=0;
        bz[start]:=true;
        while i<j do
        begin
            inc(i);
            p:=dl[i];
            for l:=en[p-1]+1 to en[p] do
            if zdl[p]+bj[l,3]<zdl[bj[l,2]] then
            begin
                zdl[bj[l,2]]:=zdl[p]+bj[l,3];
                if bz[bj[l,2]]=false then
                begin
                    bz[bj[l,2]]:=true;
                    inc(j);
                    dl[j]:=bj[l,2];
                end;
            end;
            bz[p]:=false;
        end;
        exit(zdl[finish]);
    end;
begin
    assign(input,'card.in'); reset(input);
    assign(output,'card.out'); rewrite(output);
    readln(a,b,c,d,e);
    readln(n);
    for i:=1 to n do
    begin
        readln(o,p);
        add(o-1,p,p-o+1);
        add(p,o-1,p-o+1);
    end;
    qsort(1,bs);
    len:=a+b+c+d+e;
    for i:=1 to len do
        en[i]:=en[i-1]+en[i];
    fa[1]:=a;
    fa[2]:=fa[1]+b;
    fa[3]:=fa[2]+c;
    fa[4]:=fa[3]+d;
    ans:=maxn;
    for i:=1 to zs do
        ans:=min(ans,js(fa[way[i,1]],fa[way[i,2]])+js(fa[way[i,3]],fa[way[i,4]]));
    if ans=maxn then writeln(-1)
                else writeln(ans);
    close(input);
    close(output);
end.