POJ 3608 Bridge Across Islands（旋转卡壳求凸多边形最短距离）

http://poj.org/problem?id=3608

大意：求解两个凸多边形的最短距离。

分析：依然是旋转卡壳来解决。用一对平行支撑线围绕两个凸多边形来寻找最短的距离。

计算P多边形y最小的端点和Q多边形y最大的端点，即ymin,ymax

通过ymin,ymax构造两条支撑射线LP和LQ，方向相反。两个ymin,ymax的端点的距离作为所求距离的初始值，然后旋转两条支撑线。

当满足有一条平行支撑线和凸多边形的边平行（重合）时，开始相应的判断。

判断的情况：

当有一条平行支撑线和凸多边形的边重合：

(1) 点和线段e的距离最短

(2) 点和新点的距离最短（旧点之前已经判断了）

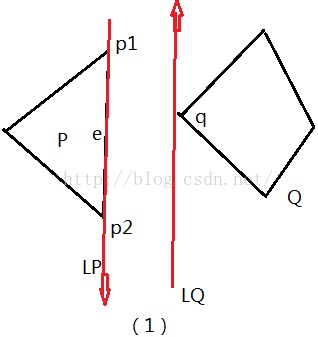
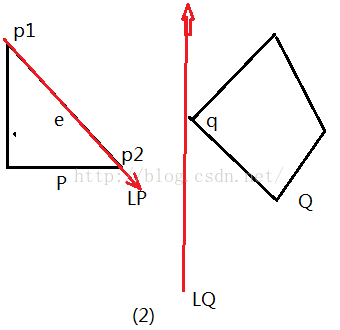
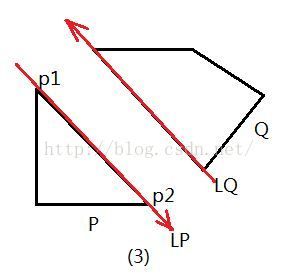
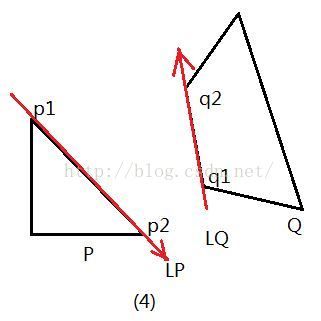
当两条平行线均和凸多边形的边重合时：

(3) 线段和线段的距离是最短的（一段距离）

(4) 最短距离产生于线段的端点的距离（四段距离）

上面的求解情况转化成 点到点的距离，点到线的距离，线到线的距离（可转化成点到线的距离）

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const double eps=1e-7,inf=1e99;
const int N=1e4+10;
struct point{
    double x,y;
};
double dis(point a,point b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

double cross(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}

double multi(point p0,point p1,point p2){  //点积 p0为角点
    return (p1.x-p0.x)*(p2.x-p0.x)+(p1.y-p0.y)*(p2.y-p0.y);
}

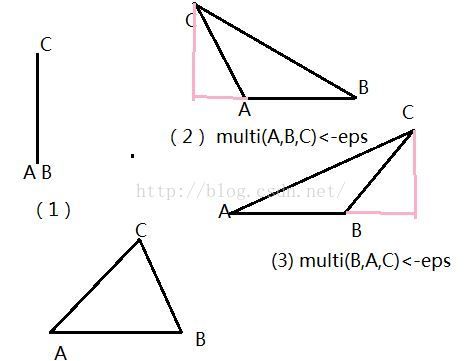
double getDis(point p0,point p1,point p2){
     if(dis(p0,p1)<eps) return dis(p2,p0);
     if(multi(p0,p1,p2)<-eps) return dis(p2,p0);
     if(multi(p1,p0,p2)<-eps) return dis(p2,p1);
     return fabs(cross(p0,p1,p2)/dis(p0,p1));  //点到线的距离
}

double minDis(point p1,point p2,point p3,point p4){
     return min(min(getDis(p1,p2,p3),getDis(p1,p2,p4)),min(getDis(p3,p4,p1),getDis(p3,p4,p2)));
}

double work(point p[],point q[],int top1,int top2){
    int ymin=0,ymax=0;
    for(int i=0;i<top1;i++){
        if(p[i].y<p[ymin].y) ymin=i;
    }
    for(int i=0;i<top2;i++){
        if(q[i].y>q[ymax].y) ymax=i;
    }
    p[top1]=p[0];
    q[top2]=q[0];
    double t,ans=inf;
    for(int i=0;i<top1;i++){
        while(t=cross(p[ymin],p[ymin+1],q[ymax])-cross(p[ymin],p[ymin+1],q[ymax+1])<-eps) ymax=(ymax+1)%top2;
        if(t>eps) ans=min(ans,getDis(p[ymin],p[ymin+1],q[ymax]));
        else ans=min(ans,minDis(p[ymin],p[ymin+1],q[ymax],q[ymax+1]));
        ymin=(ymin+1)%top1;
    }
    return ans;
}
point p[N],q[N];
int top1,top2;
int main()
{
    //freopen("cin.txt","r",stdin);
    while(cin>>top1>>top2&&(top1+top2)){
        for(int i=0;i<top1;i++){
            scanf("%lf%lf",&p[i].x,&p[i].y);
        };
        for(int i=0;i<top2;i++){
            scanf("%lf%lf",&q[i].x,&q[i].y);
        }
        printf("%.5lf\n",min(work(p,q,top1,top2),work(q,p,top2,top1)));
    }
    return 0;
}