基于Levenberg-Marquardt训练算法的BP网络Python实现
BP神经网络参考资料如下:
1、Training feed-forward networks with the Marquardt algorithm
2、The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems
3、Neural Network Design
4、http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B 中介绍的神经网络部分
以下给出Python脚本:
- import numpy as np
- from math import exp, pow
- from mpl_toolkits.mplot3d import Axes3D
- import matplotlib.pyplot as plt
- import sys
- import copy
- from scipy.linalg import norm, pinv
- class Layer:
- def __init__(self,w, b, neure_number, transfer_function, layer_index):
- self.transfer_function = transfer_function
- self.neure_number = neure_number
- self.layer_index = layer_index
- self.w = w
- self.b = b
- class NetStruct:
- def __init__(self, x, y, hidden_layers, activ_fun_list, performance_function = 'mse'):
- if len(hidden_layers) == len(activ_fun_list):
- activ_fun_list.append('line')
- self.active_fun_list = activ_fun_list
- self.performance_function = performance_function
- x = np.array(x)
- y = np.array(y)
- if(x.shape[1] != y.shape[1]):
- print 'The dimension of x and y are not same.'
- sys.exit()
- self.x = x
- self.y = y
- input_eles = self.x.shape[0]
- output_eles = self.y.shape[0]
- tmp = []
- tmp.append(input_eles)
- tmp.extend(hidden_layers)
- tmp.append(output_eles)
- self.hidden_layers = np.array(tmp)
- self.layer_num = len(self.hidden_layers)
- self.layers = []
- for i in range(0, len(self.hidden_layers)):
- if i == 0:
- self.layers.append(Layer([],[],\
- self.hidden_layers[i], 'none', i))
- continue
- f = self.hidden_layers[i - 1]
- s = self.hidden_layers[i]
- self.layers.append(Layer(np.random.randn(s, f),np.random.randn(s, 1),\
- self.hidden_layers[i], activ_fun_list[i-1], i))
- class Train:
- def __init__(self, net_struct, mu = 1e-3, beta = 10, iteration = 100, tol = 0.1):
- self.net_struct = net_struct
- self.mu = mu
- self.beta = beta
- self.iteration = iteration
- self.tol = tol
- def train(self, method = 'lm'):
- if(method == 'lm'):
- self.lm()
- def sim(self, x):
- self.net_struct.x = x
- self.forward()
- layer_num = len(self.net_struct.layers)
- predict = self.net_struct.layers[layer_num - 1].output_val
- return predict
- def actFun(self, z, activ_type = 'sigm'):
- if activ_type == 'sigm':
- f = 1.0 / (1.0 + np.exp(-z))
- elif activ_type == 'tanh':
- f = (np.exp(z) + np.exp(-z)) / (np.exp(z) + np.exp(-z))
- elif activ_type == 'radb':
- f = np.exp(-z * z)
- elif activ_type == 'line':
- f = z
- return f
- def actFunGrad(self, z, activ_type = 'sigm'):
- if activ_type == 'sigm':
- grad = self.actFun(z, activ_type) * (1.0 - self.actFun(z, activ_type))
- elif activ_type == 'tanh':
- grad = 1.0 - self.actFun(z, activ_type) * self.actFun(z, activ_type)
- elif activ_type == 'radb':
- grad = -2.0 * z * self.actFun(z, activ_type)
- elif activ_type == 'line':
- m = z.shape[0]
- n = z.shape[1]
- grad = np.ones((m, n))
- return grad
- def forward(self):
- layer_num = len(self.net_struct.layers)
- for i in range(0, layer_num):
- if i == 0:
- curr_layer = self.net_struct.layers[i]
- curr_layer.input_val = self.net_struct.x
- curr_layer.output_val = self.net_struct.x
- continue
- before_layer = self.net_struct.layers[i - 1]
- curr_layer = self.net_struct.layers[i]
- curr_layer.input_val = curr_layer.w.dot(before_layer.output_val) + curr_layer.b
- curr_layer.output_val = self.actFun(curr_layer.input_val,
- self.net_struct.active_fun_list[i - 1])
- def backward(self):
- layer_num = len(self.net_struct.layers)
- last_layer = self.net_struct.layers[layer_num - 1]
- last_layer.error = -self.actFunGrad(last_layer.input_val,
- self.net_struct.active_fun_list[layer_num - 2])
- layer_index = range(1, layer_num - 1)
- layer_index.reverse()
- for i in layer_index:
- curr_layer = self.net_struct.layers[i]
- curr_layer.error = (last_layer.w.transpose().dot(last_layer.error)) \
- * self.actFunGrad(curr_layer.input_val,self.net_struct.active_fun_list[i - 1])
- last_layer = curr_layer
- def parDeriv(self):
- layer_num = len(self.net_struct.layers)
- for i in range(1, layer_num):
- befor_layer = self.net_struct.layers[i - 1]
- befor_input_val = befor_layer.output_val.transpose()
- curr_layer = self.net_struct.layers[i]
- curr_error = curr_layer.error
- curr_error = curr_error.reshape(curr_error.shape[0]*curr_error.shape[1], 1, order='F')
- row = curr_error.shape[0]
- col = befor_input_val.shape[1]
- a = np.zeros((row, col))
- num = befor_input_val.shape[0]
- neure_number = curr_layer.neure_number
- for i in range(0, num):
- a[neure_number*i:neure_number*i + neure_number,:] = \
- np.repeat([befor_input_val[i,:]],neure_number,axis = 0)
- tmp_w_par_deriv = curr_error * a
- curr_layer.w_par_deriv = np.zeros((num, befor_layer.neure_number * curr_layer.neure_number))
- for i in range(0, num):
- tmp = tmp_w_par_deriv[neure_number*i:neure_number*i + neure_number,:]
- tmp = tmp.reshape(tmp.shape[0] * tmp.shape[1], order='C')
- curr_layer.w_par_deriv[i, :] = tmp
- curr_layer.b_par_deriv = curr_layer.error.transpose()
- def jacobian(self):
- layers = self.net_struct.hidden_layers
- row = self.net_struct.x.shape[1]
- col = 0
- for i in range(0, len(layers) - 1):
- col = col + layers[i] * layers[i + 1] + layers[i + 1]
- j = np.zeros((row, col))
- layer_num = len(self.net_struct.layers)
- index = 0
- for i in range(1, layer_num):
- curr_layer = self.net_struct.layers[i]
- w_col = curr_layer.w_par_deriv.shape[1]
- b_col = curr_layer.b_par_deriv.shape[1]
- j[:, index : index + w_col] = curr_layer.w_par_deriv
- index = index + w_col
- j[:, index : index + b_col] = curr_layer.b_par_deriv
- index = index + b_col
- return j
- def gradCheck(self):
- W1 = self.net_struct.layers[1].w
- b1 = self.net_struct.layers[1].b
- n = self.net_struct.layers[1].neure_number
- W2 = self.net_struct.layers[2].w
- b2 = self.net_struct.layers[2].b
- x = self.net_struct.x
- p = []
- p.extend(W1.reshape(1,W1.shape[0]*W1.shape[1],order = 'C')[0])
- p.extend(b1.reshape(1,b1.shape[0]*b1.shape[1],order = 'C')[0])
- p.extend(W2.reshape(1,W2.shape[0]*W2.shape[1],order = 'C')[0])
- p.extend(b2.reshape(1,b2.shape[0]*b2.shape[1],order = 'C')[0])
- old_p = p
- jac = []
- for i in range(0, x.shape[1]):
- xi = np.array([x[:,i]])
- xi = xi.transpose()
- ji = []
- for j in range(0, len(p)):
- W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
- b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
- W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
- b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C')
- z2 = W1.dot(xi) + b1
- a2 = self.actFun(z2)
- z3 = W2.dot(a2) + b2
- h1 = self.actFun(z3)
- p[j] = p[j] + 0.00001
- W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
- b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
- W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
- b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C')
- z2 = W1.dot(xi) + b1
- a2 = self.actFun(z2)
- z3 = W2.dot(a2) + b2
- h = self.actFun(z3)
- g = (h[0][0]-h1[0][0])/0.00001
- ji.append(g)
- jac.append(ji)
- p = old_p
- return jac
- def jjje(self):
- layer_number = self.net_struct.layer_num
- e = self.net_struct.y - \
- self.net_struct.layers[layer_number - 1].output_val
- e = e.transpose()
- j = self.jacobian()
- #check gradient
- #j1 = -np.array(self.gradCheck())
- #jk = j.reshape(1,j.shape[0]*j.shape[1])
- #jk1 = j1.reshape(1,j1.shape[0]*j1.shape[1])
- #plt.plot(jk[0])
- #plt.plot(jk1[0],'.')
- #plt.show()
- jj = j.transpose().dot(j)
- je = -j.transpose().dot(e)
- return[jj, je]
- def lm(self):
- mu = self.mu
- beta = self.beta
- iteration = self.iteration
- tol = self.tol
- y = self.net_struct.y
- self.forward()
- pred = self.net_struct.layers[self.net_struct.layer_num - 1].output_val
- pref = self.perfermance(y, pred)
- for i in range(0, iteration):
- print 'iter:',i, 'error:', pref
- #1) step 1:
- if(pref < tol):
- break
- #2) step 2:
- self.backward()
- self.parDeriv()
- [jj, je] = self.jjje()
- while(1):
- #3) step 3:
- A = jj + mu * np.diag(np.ones(jj.shape[0]))
- delta_w_b = pinv(A).dot(je)
- #4) step 4:
- old_net_struct = copy.deepcopy(self.net_struct)
- self.updataNetStruct(delta_w_b)
- self.forward()
- pred1 = self.net_struct.layers[self.net_struct.layer_num - 1].output_val
- pref1 = self.perfermance(y, pred1)
- if (pref1 < pref):
- mu = mu / beta
- pref = pref1
- break
- mu = mu * beta
- self.net_struct = copy.deepcopy(old_net_struct)
- def updataNetStruct(self, delta_w_b):
- layer_number = self.net_struct.layer_num
- index = 0
- for i in range(1, layer_number):
- before_layer = self.net_struct.layers[i - 1]
- curr_layer = self.net_struct.layers[i]
- w_num = before_layer.neure_number * curr_layer.neure_number
- b_num = curr_layer.neure_number
- w = delta_w_b[index : index + w_num]
- w = w.reshape(curr_layer.neure_number, before_layer.neure_number, order='C')
- index = index + w_num
- b = delta_w_b[index : index + b_num]
- index = index + b_num
- curr_layer.w += w
- curr_layer.b += b
- def perfermance(self, y, pred):
- error = y - pred
- return norm(error) / len(y)
- def plotSamples(self, n = 40):
- x = np.array([np.linspace(0, 3, n)])
- x = x.repeat(n, axis = 0)
- y = x.transpose()
- z = np.zeros((n, n))
- for i in range(0, x.shape[0]):
- for j in range(0, x.shape[1]):
- z[i][j] = self.sampleFun(x[i][j], y[i][j])
- fig = plt.figure()
- ax = fig.gca(projection='3d')
- surf = ax.plot_surface(x, y, z, cmap='autumn', cstride=2, rstride=2)
- ax.set_xlabel("X-Label")
- ax.set_ylabel("Y-Label")
- ax.set_zlabel("Z-Label")
- plt.show()
- def sinSamples(n):
- x = np.array([np.linspace(-0.5, 0.5, n)])
- #x = x.repeat(n, axis = 0)
- y = x + 0.2
- z = np.zeros((n, 1))
- for i in range(0, x.shape[1]):
- z[i] = np.sin(x[0][i] * y[0][i])
- X = np.zeros((n, 2))
- n = 0
- for xi, yi in zip(x.transpose(), y.transpose()):
- X[n][0] = xi
- X[n][1] = yi
- n = n + 1
- return X,z
- def peaksSamples(n):
- x = np.array([np.linspace(-3, 3, n)])
- x = x.repeat(n, axis = 0)
- y = x.transpose()
- z = np.zeros((n, n))
- for i in range(0, x.shape[0]):
- for j in range(0, x.shape[1]):
- z[i][j] = sampleFun(x[i][j], y[i][j])
- X = np.zeros((n*n, 2))
- x_list = x.reshape(n*n,1 )
- y_list = y.reshape(n*n,1)
- z_list = z.reshape(n*n,1)
- n = 0
- for xi, yi in zip(x_list, y_list):
- X[n][0] = xi
- X[n][1] = yi
- n = n + 1
- return X,z_list.transpose()
- def sampleFun(x, y):
- z = 3*pow((1-x),2) * exp(-(pow(x,2)) - pow((y+1),2)) \
- - 10*(x/5 - pow(x, 3) - pow(y, 5)) * exp(-pow(x, 2) - pow(y, 2)) \
- - 1/3*exp(-pow((x+1), 2) - pow(y, 2))
- return z
- if __name__ == '__main__':
- hidden_layers = [10,10] #设置网络层数,共两层,每层10个神经元
- activ_fun_list = ['sigm','sigm']#设置隐层的激活函数类型,可以设置为<span style="font-family: Arial, Helvetica, sans-serif;">tanh,radb,tanh,line类型,如果不显式的设置最后一层为line </span>
- [X, z] = peaksSamples(20) #产生训练数据点
- X = X.transpose()
- bp = NetStruct(X, z, hidden_layers, activ_fun_list) #初始化网络信息
- tr = Train(bp) #初始化训练网络的类
- tr.train() #训练
- [XX, z0] = peaksSamples(40) #产生测试数据
- XX = XX.transpose()
- z1 = tr.sim(XX) #用训练好的神经网络预测数据,z1为预测结果
- fig = plt.figure()
- ax = fig.add_subplot(111)
- ax.plot(z0[0]) #真值
- ax.plot(z1[0],'r.') #预测值
- plt.legend((r'real data', r'predict data'))
- plt.show()
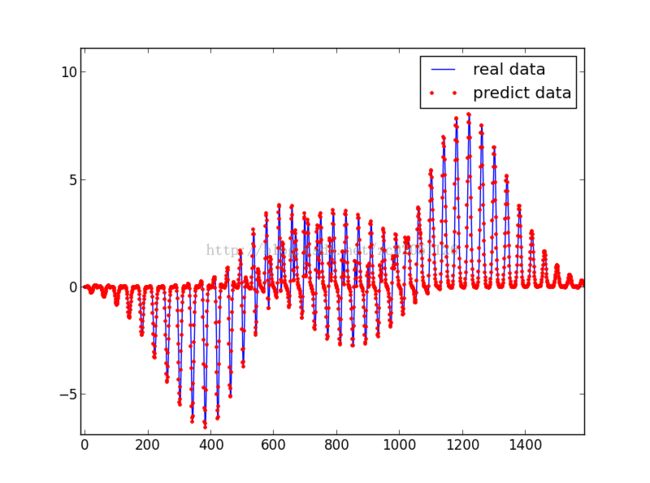
以上代码计算的结果如下图,由于初始值等原因的影响偶尔收敛效果会变差,不过大多数时候都可以收敛到下图的结果,以后再改进,欢迎指正。