后缀数组

后缀数组：后缀数组SA是一个一维数组，它保存1..n的某个排列SA[1]，SA[2]，……，SA[n]，并且保证Suffix(SA[i])<Suffix(SA[i+1])，1≤i<n。也就是将S的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA中。

名次数组：名次数组Rank[i]保存的是Suffix(i)在所有后缀中从小到大排列的“名次”。

简单的说，后缀数组是“排第几的是谁？”，名次数组是“你排第几？”。容易看出，后缀数组和名次数组为互逆运算。

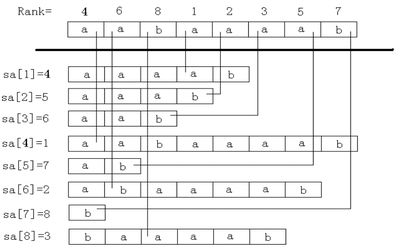
下面这张图可以很好的理解这两个数组，如图所示：

sa数组的最大用处：既是rank的互逆数组，也是保证了字符串的字典序顺序了，很多题目需要按字典序输出，而sa数组只要从1遍历到n，输出的即是按字典序的！

解释：Rank[1]=4,Rank[2]=6,Rank[3]=8依此类推（上图可知），Rank数组的下标记录的是字符串的下标，值即名次；而sa数组下标是名次，值记录的是字符串的下标。

height数组：定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

理解：suffix()其实就是Rank数组，之前看了好久才理解。但是为什么计算的是排名相邻的两个后缀的最长公共前缀呢，而不计算其他的呢？其实也挺好理解的，因为名次是按字符串的字典序排序的嘛，所以两个相邻的排名的后缀，它们的最长公共前缀才会比较长啦！不然怎么叫最长公共前缀勒，是吧！

那么对于j和k，不妨设rank[j]<rank[k],则有以下性质：
suffix(j)和suffix(k)的最长公共前缀为height[rank[j]+1],height[rank[j]+2],height[rank[j]+3],…,height[rank[k]]中的最小值。

倍增算法求sa,rank,height数组代码：

void radix(int *str,int *a,int *b,int n,int m)  
{  
    static int count[MM];  
    mem(count,0);  
    for(int i=0;i<n;i++) ++count[str[a[i]]];  
    for(int i=1;i<=m;i++) count[i]+=count[i-1];  
    for(int i=n-1;i>=0;i--) b[--count[str[a[i]]]]=a[i];  
}  
void suffix(int *str,int *sa,int n,int m) //倍增算法计算出后缀数组sa，其中sa的值即字符串的下标是从0开始的
{  
    static int rank[MM],a[MM],b[MM];  
    for(int i=0;i<n;i++) rank[i]=i;  
    radix(str,rank,sa,n,m);  
    rank[sa[0]]=0;  
    for(int i=1;i<n;i++)  
        rank[sa[i]]=rank[sa[i-1]]+(str[sa[i]]!=str[sa[i-1]]);  
    for(int i=0;1<<i<n;i++)  
    {  
        for(int j=0;j<n;j++)  
        {  
            a[j]=rank[j]+1;  
            b[j]=j+(1<<i)>=n?0:rank[j+(1<<i)]+1;  
            sa[j]=j;  
        }  
        radix(b,sa,rank,n,n);  
        radix(a,rank,sa,n,n);  
        rank[sa[0]]=0;  
        for(int j=1;j<n;j++)  
            rank[sa[j]]=rank[sa[j-1]]+(a[sa[j-1]]!=a[sa[j]]||b[sa[j-1]]!=b[sa[j]]);  
    }  
}  
void calcHeight(int *str,int *sa,int *h,int n) //求出最长公共前缀数组h  
{  
    static int rank[MM];  
    int k=0;  
    h[0]=0;  
    for(int i=0;i<n;i++) rank[sa[i]]=i;  
    for(int i=0;i<n;i++)  
    {  
        k=k==0?0:k-1;  
        if(rank[i])  
            while(str[i+k]==str[sa[rank[i]-1]+k]) k++;  
        else k=0;  
        h[rank[i]]=k;  
    }  
}