数据结构之搜索二叉树递归&非递归
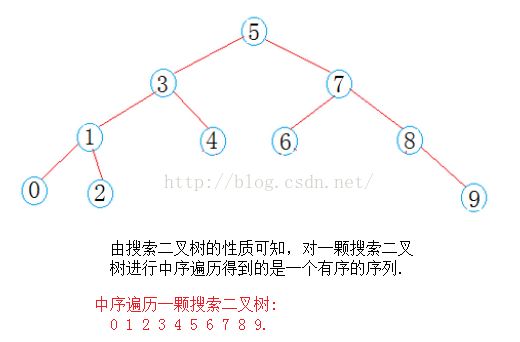
一.搜索二叉树的性质>
1). 每个节点都有一个作为搜索依据的关键码(key),所有节点的关键码互不相同。
2). 左子树上所有节点的关键码(key)都小于根节点的关键码(key).
3). 右子树上所有节点的关键码(key)都大于根节点的关键码(key)
4). 左右子树都是二叉搜索树.
类似这样的一棵树就叫做搜索二叉树:
二.搜索二叉树的基本操作
1.插入
此时我们就需要考虑三种情况:
(1).空树的情况
(2).要插入的结点已经在搜索二叉树中
(3).要插入的结点不存在搜索二叉树中.
如果是空树则直接创建结点使指向根结点的指针指向新创建的结点;如果不是空树那仫就要找到合适的位置插入,使得插入这个新的节点之后这颗树依然是一颗搜索二叉树:如果你要插入的结点的关键码比当前结点的关键码大则在右树中找到合适的位置,反之在左树中找,如果遍历完这颗树找到相同的关键码则不用处理,如果没有再次判断父关键码和要插入结点的关键码的大小,决定新的节点是插入到左子树还是右子树上.
非递归>
bool Insert(const K& key)
{
if(_root == NULL) //空树
{
_root=new Node(key);
return true;
}
Node *cur=_root;
Node *parent=NULL;
while (cur)
{
if(cur->_key < key)
{
parent=cur;
cur=cur->_right;
}
else if(cur->_key > key)
{
parent=cur;
cur=cur->_left;
}
else //已经存在相同的关键码
return false;
}
//不存在相同的关键码
if(parent->_key < key)
{
parent->_right=new Node(key);
return true;
}
else if(parent->_key > key)
{
parent->_left=new Node(key);
return true;
}
else
return false;
}
递归>
void _InsertR(Node *&root,const K& key)
{
if (root == NULL) //空树
{
root=new Node(key);
return ;
}
if (root->_key < key)
_InsertR(root->_right,key);
else if(root->_key > key)
_InsertR(root->_left,key);
}
2.删除
在搜索二叉树中最不好解决的就是删除一个结点了,根据删除结点的位置,我们需要分情况讨论:
(1).左子树为空或者右子树为空
(2).左右子树都不为空
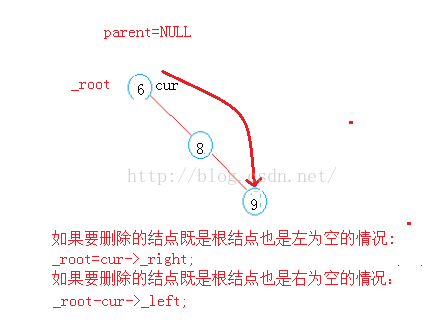
要删除一个叶子(左右子树都为空)的结点可以和左子树或者右子树为空归结为一类问题>在这里我们要考虑一种极端的情况就是你要删除的结点既是根结点也是左为空或者右为空的情况---就是出现单链的二叉树.
在删除一个结点时我们用了一个parent指针来记录当前结点的父结点,如果要删除的结点既是根结点也是左为空或者右为空的情况,此时这个parent指针就是NULL,就无法利用这个父结点了,此时我们就需要对这种情况进行处理.
要删除左右子树都不为空的结点,在这里就用到了之前实现无头单链表的删除的类似的替换思想了,可是应该用哪个节点替换呢?根据二叉搜索树的性质可知根结点的关键码一定比左子树所有的关键码都大,比右子树所有的关键码都小,要保证替换之后的根结点依然满足这样的性质,我们是否可以从当前结点的左子树中找到最大关键码的结点或者从当前结点的右子树中找到最小关键码的结点来实现呢?当然可以啦!在这里我用的替换元素是找当前结点右子树中的最小结点(在右子树中找中序遍历的第一个结点)来实现的.找到替换元素后直接交换两个结点的关键码,修改结点指针域.这样就删除了搜索二叉树中的一刻结点了.
非递归>
bool Remove(const K& key)
{
if(_root == NULL)
{
return false;
}
Node *cur=_root;
Node *parent=NULL;
while (cur)
{
if (cur->_key < key)
{
parent=cur;
cur=cur->_right;
}
else if (cur->_key > key)
{
parent=cur;
cur=cur->_left;
}
else //找到了,或者不存在
break;
}
if(cur) //存在该结点
{
if (cur->_left == NULL) //左为空
{
if(_root == cur) //删除的是根结点且左为空
_root=cur->_right;
else
{
if(parent->_right == cur)
parent->_right=cur->_right;
else if(parent->_left == cur)
parent->_left=cur->_right;
}
}
else if(cur->_right == NULL) //右为空
{
if(_root == cur) //要删除的结点是根结点且右为空
_root=cur->_left;
else
{
if(parent->_left == cur)
parent->_left=cur->_left;
else if(parent->_right ==cur)
parent->_right=cur->_left;
}
}
else //左右都不为空---用替换的方法
{
//找当前结点右树中最小的一个结点
parent=cur;
Node *tmp=cur->_right;
while (tmp->_left)
{
parent=tmp;
tmp=tmp->_left;
}
cur->_key=tmp->_key;
if(parent->_left == tmp)
parent->_left=tmp->_right;
else
parent->_right=tmp->_right;
cur=tmp;
}
delete cur;
cur=NULL;
}
return true;
}
递归>
bool _RemoveR(Node *&root,const K& key)
{
if(root == NULL)
{
return false;
}
if(root->_key < key)
return _RemoveR(root->_right,key);
else if(root->_key > key)
return _RemoveR(root->_left,key);
else
{
Node *del=root;
if (root->_left == NULL) //左子树为空
root=root->_right;
else if(root->_right == NULL) //右子树为空
root=root->_left;
else //左右子树都不为空
{
Node *parent=root;
Node *tmp=root->_right;
while (tmp->_left)
{
parent=tmp;
tmp=tmp->_left;
}
del=tmp;
root->_key=tmp->_key;
if(parent->_left == tmp)
parent->_left=tmp->_right;
else
parent->_right=tmp->_right;
}
delete del;
del=NULL;
}
return true;
}
3.查找
通过判断要查找的关键码和当前结点的关键码的大小,要查找的关键码大在右树中找,否则在左树中找.找到就返回true,否则返回false
非递归>
bool Find(const K& key)
{
Node *cur=_root;
while (cur)
{
if(cur->_key < key)
cur=cur->_right;
else if(cur->_key > key)
cur=cur->_left;
else
return true; //找到了
}
return false; //没有找到
}
递归>
bool _FindR(Node *root,const K& key)
{
if (root == NULL) //空
{
return false;
}
if(root->_key < key)
return _FindR(root->_right,key);
else if(root->_key > key)
return _FindR(root->_left,key);
else if(root->_key == key)
return true; //找到了
return false; //没有找到
}
至于源码我托管到github上了,在这里给出链接地址>https://github.com/CTTCassie/DataStructure