模型压缩与加速:(一)Octave Convolution
自AlexNet刷新了ImageNet比赛的最佳记录以来,神经网络的又一次高潮猛烈的到来了.一些列各种各样的网络层出不穷,图像/音频/文本等各种任务下都开始了神经网络一统天下的声音.然而神经网络虽然很火,近些年在落地端却鲜有比较成功的案例,其中一个很重要的原因是这些网络需要很强的计算资源,基本都要跑在PC或者服务器上.因此个人认为深度学习如果想在工业上获得比较大的推广和应用,解决模型大小与推理速度是一个很重要的问题.
模型压缩与加速自然成为了一个很重要的技术点.这个系列会写一些相关的论文和工作,记录一下一些比较实用的points,也是自我学习的总结.个人认为神经网络之所以能够被压缩和加速的同时维持足够的精度,甚至提高部分精度,其中很重要的一个原因在于模型的冗余.在实践中我们经常会感觉模型在数据集上的训练/测试精度达到存在上限,训练到达某个点metric就再也上不去了,会想当然的觉得模型的容量不够了,或者认为当前这么多参数构成的model最多就这么多表达能力了,其实不然.模型此时往往还有冗余的部分,理论上如果能对每一个权值进行精细化的调教,精度还能继续上升,或者说达到当前的精度并不需要当前这么多的参数.不是模型的表达能力不够了,仅仅是我们目前的训练方法和trick训练不出来了而已.此时模型往往还是有冗余的空间的,否则模型压缩与加速也就无从谈起了.
第一篇写的是Octave Convolution.来自Facebook和新加坡国立大学联手的文章:《Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution》.从名字就可以看出来,这是一篇针对卷及神经网络的压缩和加速文章.
这篇文章的基本想法看起来很简单但是很有意思,作者认为一张图片可以分为低频部分(粗略的结构)和高频部分(边缘纹理等细节),比如一张企鹅的照片可以按照频率如下分开:

企鹅身上的大块的毛发/大片的背景等属于低频部分,企鹅身体的边缘/企鹅与背景的交界等部分属于高频部分,这部分包含的信息变化比较多.低频的信息重复性较强,适当压缩一下不会造成很大的信息损失,而高频部分信息多样性比较强,压缩会造成信息损失.将这种想法推广到CNN网络的特征图中,特征图中的低频部分可以适当压缩,高频部分原样保留.则在不损失精度的前提下降低了模型的复杂度和计算量.这就是这篇文章的basic insight.
文章中的一张图足以用来说明上述思想.原本的特征图是 c × h × w c\times{h}\times{w} c×h×w,经过低频压缩后变为 c 1 × h × w c_1\times{h}\times{w} c1×h×w的高频部分和 c 2 × h ′ × w ′ c_2\times{h'}\times{w'} c2×h′×w′的低频部分,其中 c 1 + c 2 = c c_1+c_2=c c1+c2=c且 h ′ < h , w ′ < w h'<h, w'<w h′<h,w′<w, h ′ = 0.5 h , w ′ = 0.5 w h'=0.5h, w'=0.5w h′=0.5h,w′=0.5w文中.在进行网络的前向传播时,高低频数据除了各自传播以外还可以互相影响,保证信息的多样性.

具体做法如下:
将每个卷积核分成两个分量: W = [ W H , W L ] W=[W^H, W^L] W=[WH,WL],每一层的输入输出也分别分为两个tensor,分别代表高频特征 Y H Y_H YH和低频特征 Y L Y_L YL,前向传播时高低频信息可以相互影响, Y H = Y H → H + Y L → H Y_H=Y_{H\rightarrow{H}}+Y_{L\rightarrow{H}} YH=YH→H+YL→H, Y L = Y L → L + Y H → L Y_L=Y_{L\rightarrow{L}}+Y_{H\rightarrow{L}} YL=YL→L+YH→L.通过一个介于0~1之间的系数 α \alpha α来调节高低频通道之间的相对大小,即 c 2 = α × c , c 1 = ( 1 − α ) × c ) c_2=\alpha\times{c}, c_1=(1-\alpha)\times{c}) c2=α×c,c1=(1−α)×c), α = 0 \alpha=0 α=0时就是我们熟悉的普通卷积了.此时卷积核也要对应的分解开.需要注意的是,下图的卷积核分解和我们一般看到的卷积核示意图不同,这个长方体的厚度方向表示的卷积核的宽和高( k × k k\times{k} k×k),宽和高方向分别代表卷积核输入和输出通道按照高频和低频的分配方式.
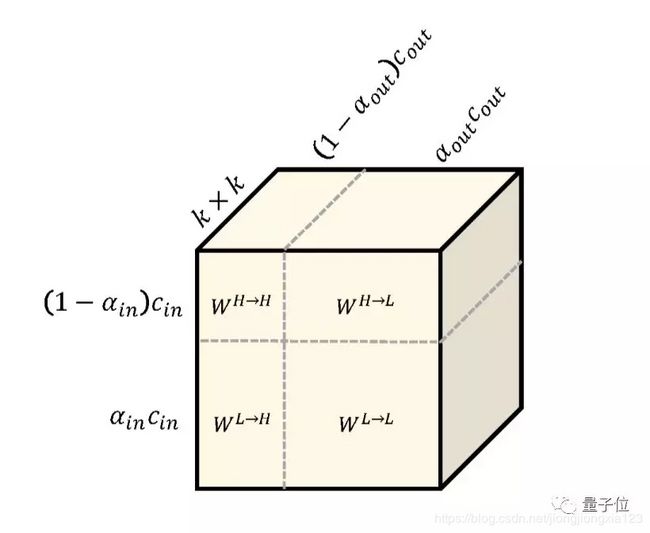
此时前向传播时特征图的计算方法如下图:
该层的输入为 ( 1 − α i n ) c i n × h × w (1-\alpha_{in})c_{in}\times{h}\times{w} (1−αin)cin×h×w的高频特征和 α i n c i n × 0.5 h × 0.5 w \alpha_{in}c_{in}\times{0.5h}\times{0.5w} αincin×0.5h×0.5w的低频特征,维度为 h × w h\times w h×w的高频特征经过 W H → H W^{H\rightarrow{H}} WH→H的卷积核运算得到 Y H → H Y^{H\rightarrow H} YH→H;维度为 0.5 h × 0.5 w 0.5h\times 0.5w 0.5h×0.5w的低频特征经过上采样得到维度为 h × w h\times w h×w的特征,再经过 W L → H W^{L\rightarrow{H}} WL→H的卷积核运算得到 Y L → H Y^{L\rightarrow H} YL→H,最后 Y H → H Y^{H\rightarrow H} YH→H+ Y L → H Y^{L\rightarrow H} YL→H得到维度为 h × w h\times w h×w的高频输出 Y H Y^{H} YH.低频特征的计算方法类似,只是第二部分使用高频输入池化降维后再通过卷积核运算.

在Octave Convolution的网络中, α \alpha α是一个可以调节的超参数,在作者的设定中,第一层的 α i n = 0 , α o u t = α \alpha_{in}=0, \alpha_{out}=\alpha αin=0,αout=α,最后一层中的 α i n = α , α o u t = 0 \alpha_{in}=\alpha, \alpha_{out}=0 αin=α,αout=0.其余层的 α i n = α o u t = α \alpha_{in}=\alpha_{out}=\alpha αin=αout=α.
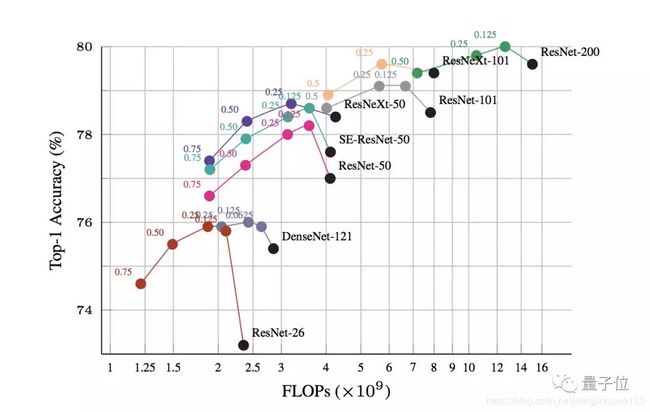
最后作者在很多网络上都做了实验,去验证了这种高低频分离的想法的有效性,在降低计算量的同时维持甚至提高了网络的精度,是非常实用的点.下图中黑色的点是原有网络的表现,可以看到,所有的网络在引入了 α \alpha α后基本都能维持精度前提下的简化,甚至简化后的model精度不降反升.
说两句题外话,有很多人diss神经网络,认为其理论基础并不完善.反正就是扔进去一堆数据一顿训练,完全是个黑箱子.我觉得这种diss也是有道理的.可以看到很多所谓的针对网络的改进,都是先给出一堆定性的描述说怎么怎么好,可是这些描述本来就很难全面的去衡量.很多东西真是怎么说都有道理,也怎么说都有缺点,反正论文就只说正面的东西,忽略不利的东西.最关键的是做实验,要拿出一些比较general的model去跑一跑,只要效果变好了那就大功告成,可以发paper了,有点成王败寇的感觉哈哈.那么这种新型的卷积到底是不是比较general的改进,是否对分类/分割/检测等各种任务都有较好的改善呢?这个就只能实际去试过才知道了吧.
论文地址:https://export.arxiv.org/abs/1904.05049
参考链接:https://mp.weixin.qq.com/s?__biz=MzIzNjc1NzUzMw==&mid=2247518961&idx=1&sn=dbecefc1a33a4271e82f67ec4d9784e0&chksm=e8d03d83dfa7b49561dfc30acbbcc326c17b02b1c84388db02e333cdf6874caf49a6cd82818f&mpshare=1&scene=1&srcid=&pass_ticket=yi%2FcpjT%2FLNaKCb0fsxUwWTuGb%2FAYHMlSjnG9ENCxVoXxSLVpOFR8YVhqEipuWIC7#rd