降维-主成分分析(PCA)

主成分分析（Principal Components Analysis）是由Hotelling于1933年首先提出的。由于多个纬度变量之间往往存在着一定程度的相关性。人们自然希望通过线性组合的方式，从这些指标中尽可能快地提取信息。当这些纬度变量的第一个线性组合不能提取更多的信息时，再考虑用第二个线性组合继续这个提取的过程，……，直到提取足够多的信息为止。这就是主成分分析的思想。

主成分分析适用于原有纬度变量之间存在较高程度相关的情况。在主成分分析适用的场合，一般可以用较少的主成分得到较多的信息量，从而得到一个更低维的向量。通过主成分既可以降低数据“维数”又保留了原数据的大部分信息。一项十分著名的案例是美国的统计学家斯通(Stone)在1947年关于国民经济的研究。他曾利用美国1929一1938年各年的数据，得到了17个反映国民收入与支出的变量要素，例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息外贸平衡等等。在进行主成分分析后，竟以97.4％的精度，用3个新变量就取代了原17个变量。

一、主成分分析的几何意义

如果仅考虑 x1 或 x2 中的任何一个分量，那么包含在另一分量中的信息将会损失，因此，直接舍弃 x1 或 x2 分量不是“降维”的有效办法。

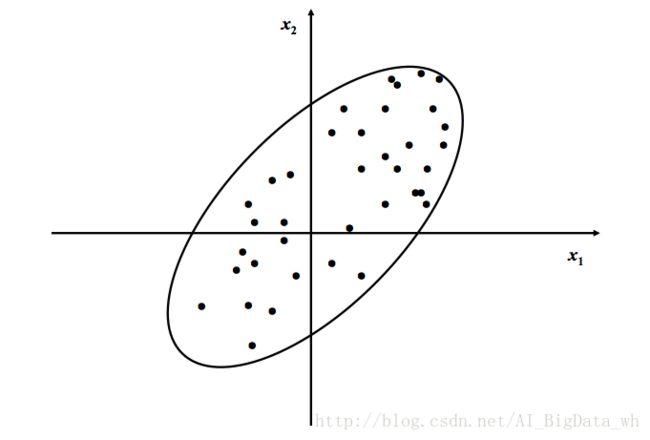
对坐标轴进行旋转， n 个点在 F1 轴上的方差达到最大，即在此方向上包含了有关 n 个样本的最大量信息。因此，欲将二维空间的点投影到某个一维方向上，则选择 F1 轴方向能使信息的损失最小。

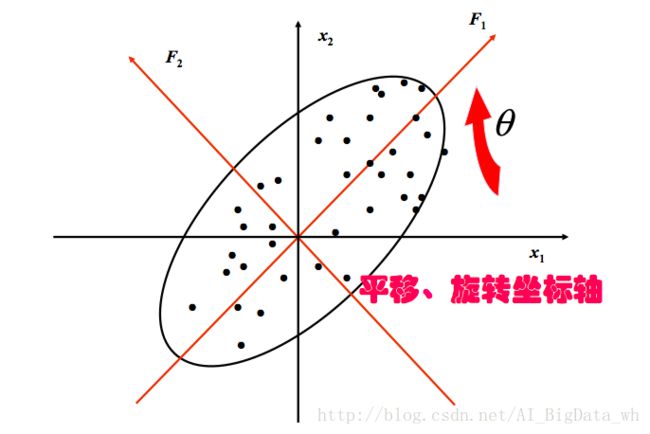
第一主成分的效果与椭圆的形状有关。椭圆越扁平， n 个点在 F1 轴上的方差就相对越大，在 F2 轴上的方差就相对越小，用第一主成分代替所有样品造成的信息损失就越小。原始变量不相关时，主成分分析没有效果

原始变量相关程度越高，主成分分析效果越好。

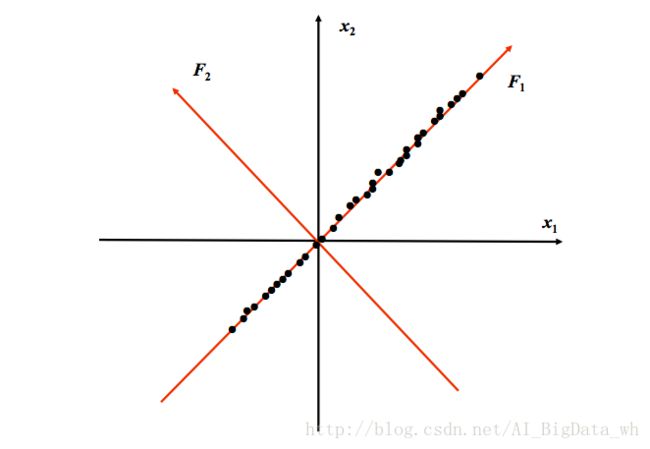
PCA的几何意义即是将原始坐标系进行旋转变换，然后将数据映射到新的坐标系，再根据一定标准去掉值较小的纬度，留下值较大的纬度–主成分。

二、主成分分析的数学模型

对于 p 维数据 xi=(xi1;xi2;…;xip) ，假定投影变换后得到的新坐标系是 {w1,w2,…,wp} ，其中 wi 是标准正交基向量（ ||wi||2=0,wTiwj=0,其中i≠j ）。若丢弃新坐标系中的部分坐标，即将数据维度降低到 p′<p ，则样本点 xi 在低维新坐标系中的投影为 x′i=(x′i1;x′i2;…;x′ip′) ，其中

x′i1x′i2x′ip′==……=w11xi1+w12xi2+…+w1pxipw21xi1+w22xi2+…+w2pxipwp′1xi1+wp′2xi2+…+wp′pxip

若基于 x′i 来重构 xi ，则会得到 x¯i=∑p′j=1x′ijwj 。考虑整个样本集 X={x1,x2,…,xm} ，原样本 xi 与基于投影重构的样本点 x¯i 之间的误差为：

∑i=1m||x¯i−xi||22=∑i=1m||∑j=1p′x′ijwj−xi||22∝−tr(WTXXTW).

根据最近重构性，上式应该被最小化，考虑到 wi 是标准正交基向量，即有主成分分析的优化目标：

minst.−tr(WTXXTW)WTW=I.

对上面优化目标使用拉格朗日乘子法可得：

XXTW=λW.

于是只需对样本集的协方差矩阵 R=XXT 进行特征值分解，将求得的特征值排序： λ1≥λ2≥…≥λp ，在取前 p′ 个特征值对应的特征向量构成 W={w1,w2,…,wp′} ，这就是主成分的解。
注：具体过程可阅读参考资料3 P230。

三、主成分求解的步骤

输入样本集 X={x1,x2,…,xm} ，主成分可以按以下步骤计算得出：
1. 计算原始变量的相关系数矩阵 R=XXT 。
2. 计算相关系数矩阵 R 的特征值，并按从大到小的顺序排列，记为

λ1≥λ2≥…≥λp

3. 计算特征值对应的特征向量，取前 p′ 个特征值对应的特征向量构成 W={w1,w2,…,wp′} 。
4. 把原始变量的值代入主成分表达式中，可以计算出主成分得分。得到的主成分得分后，可以把各个主成分看作新的变量代替原始变量，从而达到降维的目的。

四、主成分的贡献率

降维后低维空间的维数 p′ 通常由用户事先指定，不过不同的 p′ 对降维效果有很大的影响，如何靠谱地确定 p′ ？通常有两种方式：根据大于1的特征值的个数确定主成分的个数，如 p=10 ， λ1>λ2>…>λ6>1 ，那么 p′=6 ；根据主成分的累计贡献率确定主成分的个数，使累计贡献率>85%或者其他值。对于第 k 个主成分，其对方差的贡献率为：

λk∑pi=1λi

前 k 个主成分贡献率的累计值称为累计贡献率：

p′=argmink∑ki=1λk∑pi=1λi>85%或者其他值.

五、主成分分析的应用

主成分回归：即把各主成分作为新自变量代替原来自变量 x 做回归分析。还可以进一步还原得到 y 与 x 的回归方程（可以避免多重共线性的问题）。
用于综合评价：按照单个的主成分（例如第一主成分）可以对个体进行排序。按照几个主成分得分的加权平均值对个体进行排序也是一种评价方法。一般用各个主成分的方差贡献率加权。由于加权得分缺少实际意义，这种方法理论上有争议。

六、主成分分析举例

假定样本集为：

X=[x1x2x3x4]=[12213443]⇒XXT=[30282830]

相关系数矩阵对应的特征值为2和58，求得匹配的单位特征向量为：

W=⎡⎣⎢⎢⎢⎢12‾‾√12‾‾√−12‾‾√12‾‾√⎤⎦⎥⎥⎥⎥⇒WTX=⎡⎣⎢⎢⎢⎢32‾‾√12‾‾√32‾‾√−12‾‾√72‾‾√12‾‾√72‾‾√−12‾‾√⎤⎦⎥⎥⎥⎥

在新坐标系上的位置，第一维的能量 > 第二维的能量，而且它们正交。所以，如果要降到一维，无疑应该保留第一维，把第二维去掉（第1个主成分累计贡献率为96.66%）。最后得到的降维结果为：

X=[x1x2x3x4]=[32‾‾√32‾‾√72‾‾√72‾‾√]

七、主成分分析实战

scikit-learn中的主成分分析函数为decomposition.PCA，其主要包含3个参数：n_components确定要保留的主成分个数，类型为int 或者 string，缺省时默认为None，即所有成分被保留。赋值为int，比如n_components=1，将把原始数据降到一个维度。赋值为string，比如n_components=’mle’，将自动选取特征个数n，使得满足所要求的方差百分比。copy表示是否在运行算法时，将原始训练数据复制一份。若为True，则运行PCA算法后，原始训练数据的值不会有任何改变，因为是在原始数据的副本上进行运算；若为False，则运行PCA算法后，原始训练数据的值会改，因为是在原始数据上进行降维计算。whiten表示白化，即使得每个特征具有相同的方差，缺省时默认为False。

# -*- coding: utf-8 -*-

from sklearn.decomposition import PCA
import numpy as np

data = np.array([[1,1],[1.5,1.6],[2,2],[2.4,2.4],[1.95,1.9],[3,3],[3.3,3.1]])

pca = PCA(n_components=1)
newdata = pca.fit_transform(data)

print "原始数据-二维:", data
print "降维后数据-一维:", newdata

参考资料

1. http://blog.csdn.net/u012162613/article/details/42192293 scikit-learn中PCA的使用方法
2. http://scikit-learn.org/stable/auto_examples/decomposition/plot_pca_iris.html PCA example with Iris Data-set
3. https://item.jd.com/11867803.html 《机器学习》 周志华