树状数组求逆序对/ 兼板子 (有无重复数字都可)
归并排序和树状数组都可以用nlogn的算法做到求出逆序对.但这里着重讲树状数组的原理与求法.
树状数组最常用的方面就是用来求逆序对, 普通方法需要n^2的复杂度, 而树状数组只需要用nlogn的复杂度, 所以是很好的优化, 关键在于内部函数lowbit的应用.
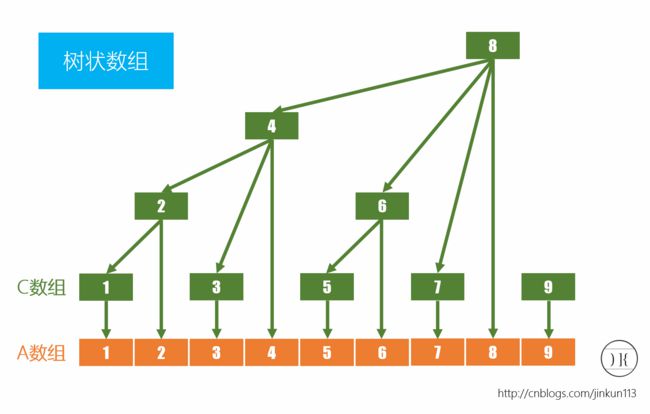
这是树状数组的结构图 : lowbit函数就是进行哪些实现之间的转化的, 因为这些数之间在二进制中存在着某种联系, 而lowbit函数便可把这些联系体现出来.!!!
最经典的栗子:
- C1 = A1
- C2 = A1 + A2
- C3 = A3
- C4 = A1 + A2 + A3 + A4
- C5 = A5
- C6 = A5 + A6
- C7 = A7
- C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
举个例子,有几个数可以通过lowbit产生0100呢?0001–lowbit–>0010–>lowbit–>0011–>lowbit–>0100,有三个数可以通过lowbit产生0100,加上它本身,总共维护了2^2个数的和。比如5(0101)没有数可以通过lowbit产生,所以维护它本身一个。6(0110)可以有5(0101)lowbit产生,所以维护两个
总之记住树状数组实现的是nlogn的算法, 和他具体实现的是什么功能就行了.
当数据的范围较小时,比如maxn=100000,那么我们可以开一个数组c[maxn],来记录前面数据的出现情况,初始化为0;当数据a出现时,就令c[a]=1。这样的话,欲求某个数a的逆序数,只需要算出在当前状态下c[a+1,maxn]中有多少个1,因为这些位置的数在a之前出现且比a大。但是若每添加一个数据a时,就得从a+1到 maxn搜一遍,复杂度太高了。树状数组却能很好的解决这个问题,可以把数一个个插入到树状数组中, 每插入一个数, 统计比他小的数的个数,对应的逆序为 i - getsum( c[i] ),其中 i 为当前已经插入的数的个数, getsum( c[i] )为比 c[i] 小的数的个数,i- getsum( c[i] ) 即比c[i] 大的个数, 即逆序的个数。最后需要把所有逆序数求和,就是在插入的过程中边插入边求和.
举个例子:有5个数,分别为5 3 4 2 1,当读入数据a=5时,c为:0,0,0,0,1;d为:0,0,0,0,1;当读入数据a=3时,c为:0,0,1,0,1;d为:0,0 , 1,1,1;当读入数据a=4时,c为:0,0,1,1,1;d为:0,0,1,2,1;
此思想的关键在于,读入数据的最大值为maxn,由于maxn较小,所以可以用数组来记录状态。当maxn较大时,直接开数组显然是不行了,这是的解决办法就是离散化。所谓离散化,就是将连续问题的解用一组离散要素来表征而近似求解的方法,这个定义太抽象了,还是举个例子吧。
假如现在有一些数:1234 98756 123456 99999 56782,由于1234是第一小的数,所以num[1]=1;依此,有num[5]=2,num[2]=3,num[4]=4,num[3]=5;这样转化后并不影响原来数据的相对大小关系,何乐而不为呢!!!
还有一点值得注意,当有数据0出现时,由于0&0=0,无法更新,此时我们可以采取加一个数的方法将所有的数据都变成大于0的.
单纯求逆序对的, 正着插求后缀和, 反着插求前缀和. (其中x的前缀和是sum[x-1])!!! (同理 x 的后缀和是sum[x+1]). 如果不是严格的逆序也就是包括等于号的话, 那么求前缀的时候 x的前缀和是sum[x] 也就是等于号啦~~~
具体看代码 : 树状数组+去重离散化
1: 倒着做求前缀和
2: 顺着做求后缀和
int c[maxn], n;
void add(int x) {
for ( ; x <= n ; x += x & -x) {
c[x]++;
}
}
int getsum(int x) {
int res = 0;
for ( ; x ; x -= x&-x) {
res += c[x];
}
return res;
}
int a[maxn];
vector<int>ve;
int getid(int x) {
return lower_bound(ve.begin(), ve.end(), x) - ve.begin() + 1;
}
void solve()
{
int k;
while(~scanf("%d%d",&n,&k)){
Fill(c,0); ve.clear();
for(int i = 1 ; i <= n ; i ++) {
scanf("%d", &a[i]);
ve.eb(a[i]);
}
sort(ve.begin(),ve.end());
ve.erase(unique(ve.begin(),ve.end()),ve.end());
ll ans = 0;
for(int i = n ; i >= 1 ; i--){
int pos = getid(a[i]);
ans += getsum(pos-1);
add(pos);
} // ans为逆序对个数
if(ans < k) printf("0\n");
else printf("%lld\n",ans-k);
}
}
离散化: 主要函数unique和lower_bound函数, 前者是去重, 后者是二分查找某个数, 返回值都是地址. 由于是二分查找, 所以必须先排序, 先记下len为unique后的数组长度, lower_bound里面也要用. 而实际上离散化后的数字来源是这个数在数组中的相对位置减去数组首地址就是类似于一个大小位置, 就用这个位置去代表这个数, 然后如果要求离散前的那个数, 直接把那个相对位置的数代回去即可. 所以,推荐用这种方式离散化.
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
vector<int >ve;
int a[maxn],n;
int getid(int x)
{
return lower_bound(ve.begin(),ve.end(),x)-ve.begin() + 1;
} //返回位置,+1代表序号从1开始算的.
void solve()
{
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
ve.push_back(a[i]);
}
sort(ve.begin(),ve.end());
ve.erase(unique(ve.begin(),ve.end()),ve.end());
for(int i=0;i<n;i++){
int v = getid(a[i]);
printf("离散前: %d 离散化后: %d \n",ve[v-1],v);
} //因为从1开始算的,所
//以v需要减个1才能映射回去.
printf("\n");
}
int main()
{
solve();
}