ZJOI一试【数列】题解--分治&dfs

【题目大意】
给你一个数n，令f(0)=0,f(1)=1,f(2i)=f(i)(i>0),f(2i+1)=f(i)+f(i+1)(i>0),让你求f(n)。

【解题报告】
此题粗略一看就想到了高精度分治，但是普通的dfs肯定是不行的，因为复杂度为O(答案)，因为答案是很大的，所以肯定会超时。那么就换一种思路来想这个问题。

如图1，f(5)由f(2),f(3)推过来，f(3)由f(1),f(2)推过来，f(2)由f(1)推过来，所以对于一个数x，我们用p表示x-1，q表示x，由前一状态向后一状态进行递归，但是在递归中不难发现要分x的奇偶进行分类讨论，如下：

① x为奇数：
如图2。

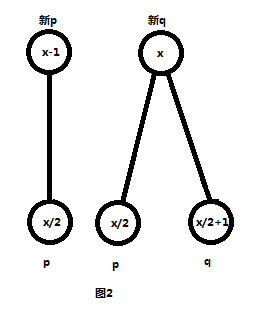
由于我们已经递归出了p,q不难发现新的p的值等于原来的p的值，而q的值则等于原来的p+q。

所以当x为奇数时p=p,q=p+q;

② x为偶数：
如图3。

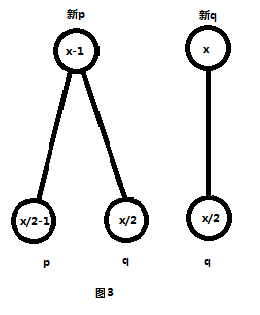
同推x为奇数时一样，只是p的值等于原来的p+q，
而q值等于原来的q的值。

所以当x为偶数时p=p+q,q=q;

综上所述：
如果x为奇数q=p+q，否则p=p+q，所以我们对于一个x，每次先dfs((x+1)/2),直到当前的x为1或0为止（x=0是因为有n=0的情况）。然后从后一状态推前一状态出答案（不难发现，q就是f(n)，所以答案就是q的值）。

时间复杂度：O(T*log2(n)*高精度)

#include
#include
#include
using namespace std;
const int maxm=105;
int t;
struct bignum
{
    int s[maxm];
    bignum operator + (bignum a) const {
        bignum c;
        memset(c.s,0,sizeof(c.s));
        c.s[0]=max(a.s[0],s[0]);
        for (int i=1; i<=c.s[0]; i++)
         c.s[i]+=s[i]+a.s[i],
         c.s[i+1]+=c.s[i]/10,
         c.s[i]%=10;
        if (c.s[c.s[0]+1]) c.s[0]++;
        while (c.s[0]>1&&!c.s[c.s[0]]) c.s[0]--;
        return c;
    }
    bignum operator + (int a) const {
        bignum c;
        memset(c.s,0,sizeof(c.s));
        c.s[0]=s[0];
        for (int i=1; i<=s[0]; i++) c.s[i]=s[i];
        c.s[1]+=a;
        for (int i=1; i<=c.s[0]; i++)
        {
            int t=c.s[i+1];
            c.s[i+1]+=c.s[i]/10;
            if (t==c.s[i+1]) break;
            c.s[i]%=10;
        }

        if (c.s[c.s[0]+1]) c.s[0]++;
        while (c.s[0]>1&&!c.s[c.s[0]]) c.s[0]--;
        return c;
    }
    bignum operator / (int a) const{
        bignum c;
        memset(c.s,0,sizeof(c.s));
        c.s[0]=s[0];
        int num=0;
        for (int i=c.s[0]; i; i--)
         num=num*10+s[i],
         c.s[i]=num/a,
         num%=a;
        if (c.s[c.s[0]+1]) c.s[0]++;
        while (c.s[0]>1&&!c.s[c.s[0]]) c.s[0]--;
        return c;
    }
}n,p,q;
inline int read_()
{
    int sum=0;
    char ch=getchar();
    while (ch<'0'||ch>'9') ch=getchar();
    while (ch>='0'&&ch<='9') sum=sum*10+ch-48,ch=getchar();
    return sum;
}
void dfs_(bignum x)
{
    if (x.s[0]==1&&x.s[1]==0) {q.s[1]=0; return;}
    if (x.s[0]==1&&x.s[1]==1) {q.s[1]=1; return;}
    dfs_((x+1)/2);
    if (x.s[1]&1) q=p+q; else p=p+q;
}
void work_()
{
    n.s[0]=0; char ch=getchar();
    while (ch<'0'||ch>'9') ch=getchar();
    while (ch>='0'&&ch<='9') n.s[++n.s[0]]=ch-48,ch=getchar();
    for (int i=1; i<=n.s[0]/2; i++) swap(n.s[i],n.s[n.s[0]-i+1]);
    p.s[0]=q.s[0]=1; p.s[1]=0;
    dfs_(n);
    for (int i=q.s[0]; i; i--) putchar(q.s[i]+48); putchar(10);
}
int main()
{
    freopen("sequence.in","r",stdin);
    freopen("sequence.out","w",stdout);
    t=read_();
    for (int i=1; i<=t; i++) work_();
    return 0;
}