数据结构与算法分析：算法设计技巧

算法设计技巧

贪婪算法

顾名思义，贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

用背包问题来介绍贪心算法：

背包问题：有一个背包，背包容量是M=150。有7个物品，物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大，但不能超过总容量。

物品 A B C D E F G

重量 35 30 60 50 40 10 25

价值 10 40 30 50 35 40 30

分析如下

目标函数： ∑pi最大

约束条件是装入的物品总重量不超过背包容量：∑wi<=M( M=150)。

（1）根据贪心的策略，每次挑选价值最大的物品装入背包，得到的结果是否最优？

（2）每次挑选所占重量最小的物品装入是否能得到最优解？

（3）每次选取单位重量价值最大的物品，成为解本题的策略。

值得注意的是，贪心算法并不是完全不可以使用，贪心策略一旦经过证明成立后，它就是一种高效的算法。

贪心算法还是很常见的算法之一，这是由于它简单易行，构造贪心策略不是很困难。

可惜的是，它需要证明后才能真正运用到题目的算法中。

一般来说，贪心算法的证明围绕着：整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。

对于背包问题中的3种贪心策略，都是无法成立（无法被证明）的，解释如下：

贪心策略：选取价值最大者。反例：

W=30

物品：A B C

重量：28 12 12

价值：30 20 20

根据策略，首先选取物品A，接下来就无法再选取了，可是，选取B、C则更好。

（2）贪心策略：选取重量最小。它的反例与第一种策略的反例差不多。

（3）贪心策略：选取单位重量价值最大的物品。反例：

W=30

物品：A B C

重量：28 20 10

价值：28 20 10

根据策略，三种物品单位重量价值一样，程序无法依据现有策略作出判断，如果选择A，则答案错误。但是果在条件中加一句当遇见单位价值相同的时候,优先装重量小的,这样的问题就可以解决.

所以需要说明的是，贪心算法可以与随机化算法一起使用，具体的例子就不再多举了。（因为这一类算法普及性不高，而且技术含量是非常高的，需要通过一些反例确定随机的对象是什么，随机程度如何，但也是不能保证完全正确，只能是极大的几率正确）。

 

分治算法

在计算机科学中，分治法是一种很重要的算法。字面上的解释是"分而治之"，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并 。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

    任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。例如，对于n个元素的排序问题，当n=1时，不需任何计算。n=2时，只要作一次比较即可排好序。n=3时只要作3次比较即可，…。而当n较大时，问题就不那么容易处理了。要想直接解决一个规模较大的问题，有时是相当困难的。分治法在每一层递归上都有三个步骤：

step1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；

step2 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题

step3 合并：将各个子问题的解合并为原问题的解。

二分查找就是最典型的分治算法

动态规划

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

 

与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）

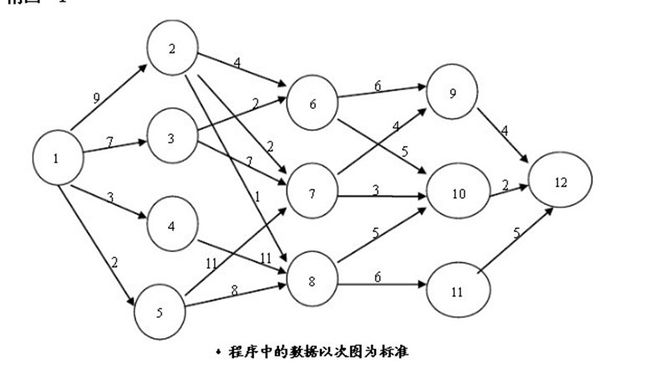
多段图决策问题

对多段图，求最短路径，如图：

对其使用动态规划法：

阶段：将图中的顶点划分5个阶段，k

状态：每个阶段有几种供选择的点s

决策：当前状态应在前一个状态的基础上获得。决策需要满足规划方程

规划方程：f(k)表示状态k到终点状态的最短距离。

初始条件：f(k)=0;

方程：f(k-1)=min{f(k)+W(k-1,k)}其中W(k-1,k)表示状态k-1到状态k的距离

 

随机化算法

随机化算法是这样一种算法，在算法中使用了随机函数，且随机函数的返回值直接或者间接的影响了算法的执行流程或执行结果。随机化算法基于随机方法，依赖于概率大小。

快速排序

在快速排序中，选择枢纽元时，可以考虑使用随机数来决定枢纽元，这样可以由输入依赖转化为随机数依赖，更好。

回溯算法

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就"回溯"返回，尝试别的路径。

   回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为"回溯点"。

     许多复杂的，规模较大的问题都可以使用回溯法，有"通用解题方法"的美称。

家具选择问题

选择家具的摆放，包含许多种尝试的可能性，当摆放到某一步，如果该步后面的都不理想，则返回到这步。