《统计学习方法》笔记（二）感知器

感知机是二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值，属于判别模型。

感知机学习旨在求出将训练数据进行线性划分的分离超平面，感知机是神经网络与支持向量机的基础。

假设输入空间（特征空间）是X∈Rn，输出空间是Y={+1, -1}。输入x∈X表示实例特征向量。对应于输出空间（特征空间）的点：输出y∈Y表示实例类别，由输入空间到输出空间的如下函数：

f(x) = sign(w*x+b)

称为感知机。其中w和b是感知机模型参数。w是权值，b是偏置。感知机是一种线性分类模型，属于判别模型。

Sign（x）是符号函数，x>=0 为+1,x<0为-1.

感知机sign(wx+b)的损失函数可以简写为：  其中M是误分类点集合，这个损失函数称为感知机经验风险函数。

感知机学习算法是误差驱动的，具体采用随机梯度下降法。随机一个选取一个误分类点（xi, yi）对w和b进行更新。

 η（0<=η<=1）是步长，统计学习中称为学习率。通过不断迭代，损失函数不断减小，直到为0。 具体步骤： 1、 随机选取w0和b0 2、 在训练数据中选取（xi，yi） 3、 如果yi(w*xi+b) <= 0  4、 转2，直到训练数据中，没有误分类点。 感知机学习算法直观的解释如下： 当一个实例点被误分类时，即位于分离超平面错误的一边，则调整w和b使得超平面想误分类点一侧移动，减少误分类点到超平面的距离。直到超平面越过该误分类点，被正确分类。

 

 

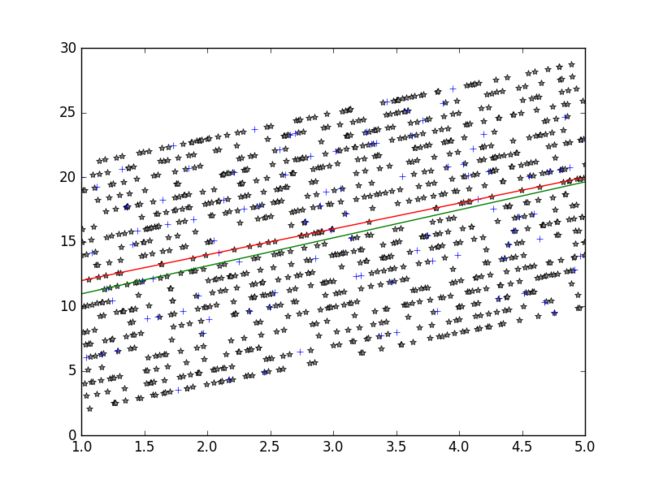
from random import randint
import numpy as np
import matplotlib.pyplot as plt


class TrainDataLoader:
    def __init__(self):
        pass
    def GenerateRandomData(self, count, gradient, offset):
        x1 = np.linspace(1, 5, count)#在指定的间隔内返回均匀间隔的数字
        x2 = gradient*x1 + np.random.randint(-10,10,*x1.shape)+offset
        dataset = []
        y = []
        for i in range(*x1.shape):
            dataset.append([x1[i], x2[i]])
            real_value = gradient*x1[i]+offset
            if real_value > x2[i]:
                y.append(-1)
            else:
                y.append(1)
        return x1,x2,np.mat(y),np.mat(dataset)


class SimplePerceptron:
    def __init__(self, train_data = [], real_result = [], eta = 1):
        self.w   =   np.zeros([1, len(train_data.T)], int)
        self.b   =   0
        self.eta =   eta
        self.train_data   = train_data
        self.real_result  = real_result
    def nomalize(self, x):
        if x > 0 :
            return 1
        else :
            return -1
    def model(self, x):
        # Here are matrix dot multiply get one value
        y = np.dot(x, self.w.T) + self.b
        # Use sign to nomalize the result
        predict_v = self.nomalize(y)
        return predict_v, y
    def update(self, x, y):
        # w = w + n*y_i*x_i
        self.w = self.w + self.eta*y*x
        # b = b + n*y_i
        self.b = self.b + self.eta*y
    def loss(slef, fx, y):
        return fx.astype(int)*y#实现变量类型转换

    def train(self, count):
        update_count = 0
        while count > 0:
            # count--
            count = count - 1

            if len(self.train_data) <= 0:
                print("exception exit")
                break
            # random select one train data
            index = randint(0,len(self.train_data)-1)
            x = self.train_data[index]
            y = self.real_result.T[index]#其实就是对一个矩阵的转置
            # wx+b
            predict_v, linear_y_v = self.model(x)
            # y_i*(wx+b) > 0, the classify is correct, else it's error
            if self.loss(y, linear_y_v) > 0:
                continue
            update_count = update_count + 1
            self.update(x, y)
        print("update count: ", update_count)
        pass#pass就是什么也不做,只是为了防止语法错误
    def verify(self, verify_data, verify_result):
        size = len(verify_data)
        failed_count = 0
        if size <= 0:
            pass
        for i in range(size):
            x = verify_data[i]
            y = verify_result.T[i]
            if self.loss(y, self.model(x)[1]) > 0:
                continue
            failed_count = failed_count + 1
        success_rate = (1.0 - (float(failed_count)/size))*100
        print("Success Rate: ", success_rate, "%")
        print("All input: ", size, " failed_count: ", failed_count)

    def predict(self, predict_data):
        size = len(predict_data)
        result = []
        if size <= 0:
            pass
        for i in range(size):
            x = verify_data[i]
            y = verify_result.T[i]
            result.append(self.model(x)[0])
        return result



if __name__ == "__main__":
    # Init some parameters
    gradient = 2
    offset   = 10
    point_num = 1000 #点的个数
    train_num = 50000
    loader = TrainDataLoader()
    x, y, result, train_data =  loader.GenerateRandomData(point_num, gradient, offset)#训练集
    x_t, y_t, test_real_result, test_data =  loader.GenerateRandomData(100, gradient, offset)#测试集

    # First training
    perceptron = SimplePerceptron(train_data, result)
    perceptron.train(train_num)#训练次数
    perceptron.verify(test_data, test_real_result)
    print("T1: w:", perceptron.w," b:", perceptron.b)

    # Draw the figure
    # 1. draw the (x,y) points
    plt.plot(x, y, "*", color='gray')
    plt.plot(x_t, y_t, "+")
    # 2. draw y=gradient*x+offset line
    plt.plot(x,x.dot(gradient)+offset, color="red")
    # 3. draw the line w_1*x_1 + w_2*x_2 + b = 0
    plt.plot(x, -(x.dot(float(perceptron.w.T[0]))+float(perceptron.b))/float(perceptron.w.T[1])
             , color='green')
    plt.show()

update count: 3343Success Rate: 100.0 %All input: 100 failed_count: 0T1: w: [[-142.68368368 64.63263263]] b: [[-571]]

值得注意的是每一次运行的结果都不一致，存在很多姐，如果想要得到唯一的超平面，需要对分离超平面增加约束条件。