深度学习与计算机视觉系列(下)--目标检测&图像分割
深度学习与计算机视觉入门系列(下)
数据嗨客最近发布了一个深度学习系列,觉得还不错,主要对深度学习与计算机视觉相关内容做了系统的介绍,看了一遍,在这里做一下笔记。
目录
-
- 深度学习与计算机视觉入门系列(下)
- 目录
- 深度学习第8期:深度学习的常见框架
- 深度学习第9期:强化学习的基本概念
- 深度学习第10期:基于Q的强化学习(上)
- 深度学习第11期:基于Policy的强化学习
- 深度学习第12期:深度学习的应用 综述
- 1、卷积神经网络与计算机视觉
- 2、循环神经网络与自然语言处理
- 3、生成模型
- 4、强化学习
- 深度学习第13期:目标检测问题
- 滑动窗口检测器
- R-CNN、Fast R-CNN和Faster R-CNN
- R-FCN
- 单次检测方法
- 深度学习第14期:图像分割问题
- 图像分割的传统方法
- 上采样
- U-Net
- 深度学习与计算机视觉入门系列(下)
深度学习第8期:深度学习的常见框架
深度学习框架也可以就其抽象的程度分为抽象程度较高的“前端框架”与抽象程度较低的“后端框架”。
“前端框架“主要有Keras与Gluon,它们的主要特点是容易上手。如果你想快一些在一些数据集上使用深度学习的模型,看看其威力的话,先学会一个“前端框架”是不错的选择。学会了前端框架之后,你往往可以只用四五行的代码就写出一个神经网络,然后,就可以将其用在你的数据集上了。
“后端框架”有Theano、TensorFlow、Torch、Caffe、MXNet、Neon 和 CNTK这七种。
深度学习第9期:强化学习的基本概念
2016年,AlphaGO击败人类的围棋冠军李世石,运用的就是强化学习的技术(那是一个监督学习加强化学习的版本)。这一事件也吸引了大众对于强化学习,乃至整个深度学习领域的广泛关注。而去年的AlphaZero则通过完全强化学习的方式,用更短的时间击败了AlphaGo,则再一次让人们开了眼界。
在某个游戏或者某个特定的任务规则中,有许多种state(简记为s),我们有许多种action(简记为a)可以采取。在某一个回合中,当我们在某一个s上采取了一个a之后,(s,a)就会在(一定概率的意义下/确定意义下)导致我们进入下一个s,并同时获得一个reward(简记为r),循环往复,直到达到某一个done(回合结束的标志)之后,一个回合结束。可以开始下一个回合。
也就是说,我们的训练集应该由很多个回合的数据组成,而每一个回合由![]() 组成。我们要用这样的数据来训练一个agent,使得它在s中能够最好地找出a,使我们获得的r最大。例如,下一盘象棋就可以转换为一回合的数据。
组成。我们要用这样的数据来训练一个agent,使得它在s中能够最好地找出a,使我们获得的r最大。例如,下一盘象棋就可以转换为一回合的数据。
深度学习第10期:基于Q的强化学习(上)
深度学习第11期:基于Policy的强化学习
深度学习第12期:深度学习的应用 综述
卷积层是一种适合处理图像数据的结构,故而在所有涉及到图像数据的领域,我们都要用到卷积层;RNN的循环结构适用于时间序列,所以只要有时间序列性质的数据出现,我们就可以用到循环的结构。对于视频数据,由于它既有图像的性质,又有时间序列的性质,所以我们设计的网络往往会同时含有卷积层与循环连接。
为了解决一个具体的问题,我们往往需要多个模型协同合作。如果我们要设计一个无人车,我们就首先需要让车能够智能地识别路况。我们设计一个目标检测的网络可以将摄像头捕捉到的街景中包含哪些物体告诉我们。但是,这样一张静态的图片对于我们了解路上发生了什么毫无意义,所以我们需要把按一定时间间隔采样的目标检测的结果进一步分析,才能得到实时的路况信息。这个部分的模型可以和前一个部分的目标检测问题相分离;而我们又要设计一个模型对于实时的路况信息进行决策,这又可以和前面的模型相分离。比如我们可以设计一个算法,根据一些规则对路况进行决策,我们也可以选择采用强化学习的方法,纯粹通过学习来得出无人车的驾驶技巧。在工业界,我们一般将一个大的具体问题分为几个部分,每一个部分都是含义清晰的问题,有许多具体的模型可以采用,分为几个组来完成。这样,就能真正将深度学习用于实际问题。
1、卷积神经网络与计算机视觉
分类(classification)是CV领域最为经典的问题之一,也是CNN崛起之后第一个广泛运用的领域。但是在实际中,分类问题的应用领域较少。应用较多的主要是目标检测与语义分割这两种问题。它们在不同的领域有着广泛的应用。
目标检测:
面对定位或者目标检测问题,我们需要设计如下形式的CNN:输入为一张图片,输出为一组或多组的定位坐标或分类向量。
目标检测是一个十分实用的领域。例如,在我们日常用手机照相的时候,手机会出现一个框来定位人脸,这就属于目标检测的领域。此外,目标检测还可以用于智能监控等等方面。

语义分割:
面对分割问题,我们要设计一种特殊的CNN:其输入是一张图片,输出为一个与原图片同样大小的张量,标记了原图片每一个对应位置的类别(也是用属于各个类别的概率向量表示)。
目前,分割问题在许多领域都有广泛的应用。例如,在医学图像的领域,对于B超这样的影像图片,传统上只能通过经验丰富的医生仔细看,然后人为地识别照片中哪一块组织有什么样的问题。但是现在由于有了深度学习的技术,我们可以将医学影像直接输入深度学习的模型,使之快速地得出结果。目前,深度学习在很多疾病的诊断上准确率已经超过了经验丰富的医生。而从效率而言,其更是比医生快了不知多少倍。随着这些技术逐步投入使用,人类的医疗水平与生存质量将得到极大的改观。这也是深度学习造福人类的例子之一。

此外,在CV领域,例如去噪声、图片生成等领域,各种CNN的模型也有广泛的应用。
2、循环神经网络与自然语言处理
3、生成模型
4、强化学习
深度学习第13期:目标检测问题
我们利用前面介绍的CNN的组件,再使用一些trick将这些基本组件相连在一起,设计一个具有足够表示能力,可以训练的CNN,就可以解决分类的问题。
与分类问题相比,目标检测与分割问题更加复杂。
在目标检测问题中,我们要在图片中找出具体物体的位置,并且标出其类别;而在分割问题中,我们要为每一个像素点都标记出其所属的类别。为此,我们必须要采用比分类模型更加复杂的模型。
目标检测问题主要有两大类模型,一类是R-CNN(即先确定候选区域,再进行分类与定位),另外一类是单次检测方法。我们下面将分别介绍这两类模型;
在分割问题中,我们也有许多模型,我们将介绍一种比较常用的模型——U-Net。
滑动窗口检测器
当CNN在图像分类问题中取得了巨大成功之后,人们自然地想要将其运用于目标检测领域。一个朴素的想法就是,将分类问题的CNN直接运用到目标检测问题上。基于这种想法就诞生了如下的滑动窗口法:

这是一种极其朴素而繁琐的方法,就是选用不同长宽大小的窗口,依次划过图像,将窗口中截取的部分图像输入分类CNN。如果某一个窗口截取的图像被分类CNN以很高的置信度判别为某一物品,则我们判断该位置有一个物品。
这种方法无疑是十分低效的。因为要用不同大小的窗口,每一个窗口又要从左到右、从上到下地滑动,这会生成大量的候选区域。我们必须使用其它方法,以提升效率。
R-CNN、Fast R-CNN和Faster R-CNN
采用选择性搜索的方法,选择候选区域,而不是滑动窗口一样的暴力搜索。
包含两部分:
1、找出尽量精准合适的候选区域;
2、对候选区域内容分类;
R-CNN(Region-CNN)就是基于这样的思想设计的——首先生成候选区域,然后将其放入一个CNN中进行特征提取。在输出端,一方面将其连接一个分类器(一般采用SVM)确定目标的类别,另一方面将其连接一个回归器,进一步确定边框的合适位置,即找出“刚刚好”框住目标的边框。其结构示意图如下:
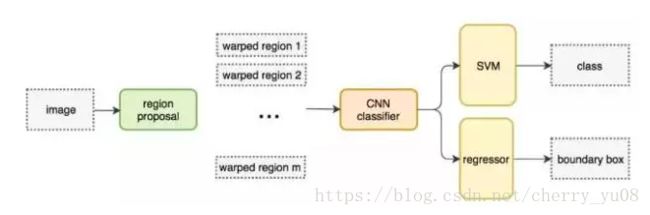
在R-CNN中,由于输入的图片是十分高维的,所以用选择性搜索法寻找候选区域是一个计算量十分巨大的步骤。
Fast-R-CNN则在此基础上进行了改进——它首先让输入的图片通过一定个CNN,使其得到降维。然后再在降维后的feature map上生成候选区域。观察下面的示意图,我们不难发现它与R-CNN的区别:
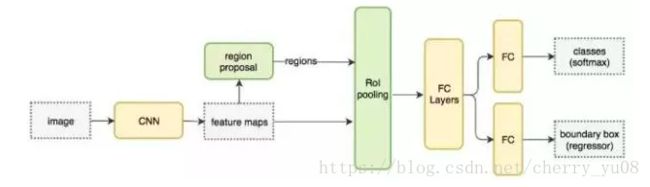
Faster R-CNN又在Fast R-CNN的基础上进行了进一步的改进。它让图片首先通过一个CNN,变成feature map。然后,它不像Fast R-CNN一样用普通的选择性搜索来生成候选区域。它是直接训练一个专门的神经网络(称作候选区域网络,Region Proposal Network,简称RPN),来寻找候选区域。
基于RPN,我们就可以设计出Faster R-CNN。其整体的原理示意图如下:
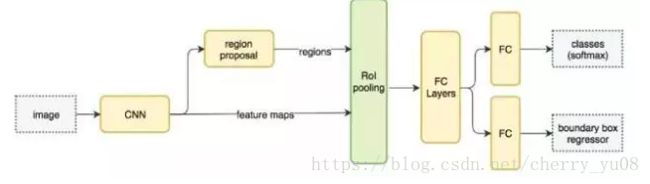
下面,我们再用一组更为立体的示意图来呈现三者的区别,有助于读者进一步理解。
以下是R-CNN:

以下是Fast R-CNN:
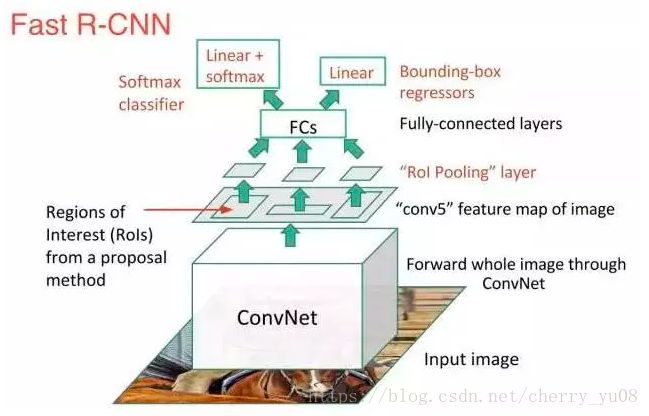
以下是Faster R-CNN:

总的来说,R-CNN,Fast R-CNN与Faster R-CNN都属于同一类方法——它们都是首先先生成一系列候选区域,然后再分别对候选区域进行分类以检测目标,进行回归以进一步确定“刚刚好”框住目标的边框。
R-FCN
在使用Faster R-CNN进行目标检测时,每张图片几乎要生成2000个感兴趣的区域(以下简称为ROI),R_FCN希望减少ROI,使计算量变少。
论文《R-FCN: Object Detection via Region-based Fully Convolutional Networks》
单次检测方法
在上述的R-CNN系列方法中,我们总是要分两步,先确定候选区域ROI,再将其输入一个CNN进行分类与边框的调整。即使Faster R-CNN比R-CNN快了几乎两个数量级,它分两步的结构仍然会使检测速度不够快。在R-FCN中,我们也是分两步。不过确定ROI之后,我们对于每个ROI不需要用CNN计算,只需要用一个平均池化(average pooling),这使速度大大加快了。但是,如果要对一个图片中2000个ROI都进行平均池化,时间成本仍然不能忽视。所以,我们自然想到能否发明一种算法,只用一个步骤完成目标检测?事实上,SSD(Single-Shot Detector)与YOLO(You Only Look Once)都是根据这种思想设计而成的。这些算法一般比R-CNN系列的算法更快(训练时间可能更长,但是对于图片算出检测结果的时间要短许多)。
YOLO:
回顾我们最初介绍的滑动窗口检测方法。它实际上是一种十分简单直接的办法。但是,它的致命问题在于它给出的候选区域太多,导致计算成本巨大。事实上,滑动窗口检测法的致命缺点在于,它直接把候选区域当成是“刚刚好”框住目标的方框,而只是检测方框内的物品类别。这也就是说,它必须有大量的候选区域,才能保证这些候选区域中存在“刚刚好”框住目标的区域。
在R-CNN中,我们采用了调整边框的技术。这让我们想到,我们可以不必采用太多的候选区域。我们可以只选用较少量的候选区域作为初始的猜想,然后再用回归技术确定最后的边框。注意到在R-CNN中,我们还是用了比较多的计算量来确定候选区域。这意味着,我们的候选区域中,即使没有“刚刚好”框住目标的,也包含“差不多”框住目标的。而在单次检测方法中,我们则进一步放宽。我们减少找ROI的计算量,只用找出“勉强”框住目标的边框即可,然后,我们再花费更多计算在调整边框上。
将这种思想贯彻到极致,我们的想法是直接将图片分成7×7的区域,作为候选区域。这样一来,我们就不需要任何的计算量来确定候选区域了。但是这样一来,“勉强”框住目标的这个“勉强”就被放的有些宽(有些“太勉强了”)。所以,调整边框需要更多的计算量。在YOLO中,7×7的候选区域负责预测中心在它们之中的目标。例如下图中,红色的候选区域要负责预测狗。也就是说,我们认为红色区域是“勉强”框住狗的,然后再将其调整为黄色的边框。

深度学习第14期:图像分割问题
图像分割的传统方法
传统上,为了对一个像素分类,使用该像素周围的一个图像块作为CNN的输入用于训练和预测。依次对每一个像素点都进行这种分类,则完成了对整个图片的分割。
但是这种方法有几个缺点:一是存储开销很大。例如对每个像素使用的图像块的大小为15x15,然后不断滑动窗口,每次滑动的窗口给CNN进行判别分类,因此所需的存储空间根据滑动窗口的次数和大小急剧上升。二是计算效率低下。相邻的像素块基本上是重复的,针对每个像素块逐个计算卷积,这种计算也有很大程度上的重复。三是像素块的大小限制了感知区域的大小。通常像素块的尺寸比整幅图像的尺寸小很多,只能提取一些局部的特征,从而导致分类的性能受到限制。
下面,我们来介绍深度学习做图像分割的主要办法——U-Net。它可以很好地解决上述的问题,即能够使得每个像素的分类尽可能考虑全局信息,也要尽量节约计算量。不过在此之前,我们要先介绍一种上采样的技术。U-Net中会用到这种技术。
上采样
在普通的CNN中,为了降维,我们会采用下采样。常见的下采样包括pooling、subsample以及使用带有stride的卷积(相当于先采用stride=1的卷积然后再进行subsample)。通过下采样,我们可以对每一个k×k的方块只找出一个元素做为代表元,以达到降维的目的。
而这里,我们要考虑如何才能实现上采样。即如何从1个元素中生成出k×k个元素。常见的上采样都是通过转置卷积(transpose convolution)实现的。
由于卷积是线性的,所以我们能够将其转化为仿射变换,即矩阵的乘积。而矩阵自然是可以转置的,这也就让我们自然想到如下问题:如果将一个卷积核K对应于一个矩阵A,找它的转置为A’,它也对应于一个矩阵乘积运算。如果将这个矩阵运算对应回一个卷积核K’,K’会是怎么样的呢?
首先要注意到的是,如果一个卷积核K,某一维输入的长度i,输出长度o,则卷积核K’应该以o为输入长度,i为输出长度。如果原来的卷积核把输入变小了,则转置卷积核会把输入变大作为输出。
下面,我们来看stride与zero padding在转置下分别会发生哪些变化:
假定卷积核K的kernel size=k,stride=1,而zero padding=p(p取值范围为0到k-1),则卷积核K’的kernel size为k,stride=1,而zero padding=k-p-1。也就是说,越大的zero padding在转置后会变得越小,越小的zero padding在转置之后会变得越大。
我们假设卷积核为(A,B,C),则其对应的一维卷积的矩阵,以及其卷积如下所示:

下面我们再来看看stride在转置下是什么:
假定卷积核K的kernel size=k,zero padding=0,而stride=s,则卷积核K’的kernel size为k,stride为1/s。这被称作fractionally strided convolutions(分数stride卷积),它就相当于,kernel每一次往右滑动1/s步。就具体操作而言,它是首先在输入的任意两个元中插入s-1个元素,使得输入扩大s倍,然后再进行stride=1的卷积。
一维的fractionally strided convolutions示例如下:
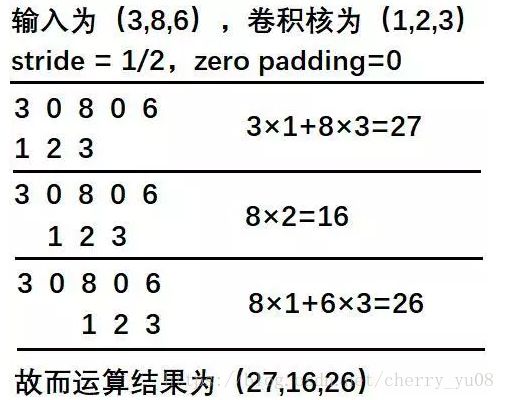
二维的分数stride卷积示意图如下(输入的蓝色元素被拆开扩大后进行卷积):

与zero padding类似,越大的stride在transpose之后会变得越小,越小的stride在transpose之后变得越大。不过zero padding是一种加减的关系,而stride是一种乘除的关系。所以从上采样的角度而言,无疑stride是更加有意义的。
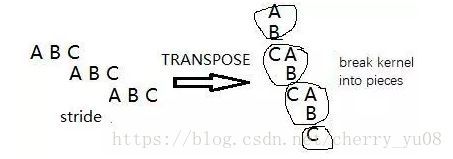
此外,我们还可以用另一种角度来看分数stride卷积——我们可以想象它是将一个卷积核给拆开成为几份。如下是示意图,假设有一个一维卷积,卷积核为(A,B,C),则stride=2的卷积对应的矩阵,以及该矩阵的转置如下图所示:
U-Net
在分割问题中,我们期望输入与输出在空间尺度上具有同样的大小。例如当我们的输入是一个128×128×3(3为通道数)的图片,有20种候选类别的时候,我们希望输出一个128×128×20的张量,表示每一个像素属于各个类别的概率。
对于每一个具体的像素而言,其属于哪一个类别,不但与其本身的性质有关,更加与其旁边的像素的性质有关,它在整个图片结构中的地位有关。所以,我们必须要提取出图片中的宏观结构,才能更好地对区域进行划分。但是另一方面,由于分割问题中确定具体边界的位置也是很重要的,所以我们也要保持住像素的细节,保持微观的信息。
在一般分类问题的CNN中,随着输入的前传,我们逐渐提取了宏观的信息,而舍弃了微观的信息。而在分割问题中,我们则希望在不丢失微观信息的情况下,提取宏观信息。最后,我们希望输出的结果中既考虑到微观信息,也考虑到宏观信息。U-Net的结构正是根据这种需求而设计出来的。
在U-Net中,从输入端到输出端可以分为两个阶段。第一个阶段被称作编码,第二个阶段被称作解码。第一个阶段中,我们逐渐使用卷积与pooling,将输入降维,以提取出图片的宏观信息。而在第二个阶段中,我们则需要使用上一节介绍的特殊卷积(up-conv)让feature map逐渐地变大,变回原来的大小。然而,由于pooling会导致丢失信息,所以即使采用up-conv,也无法让第一阶段丢失的微观信息重新出现。为此,我们要使用skip connection,从第一阶段的编码器中直接提取信息,将其传递到解码器中。这样,U-Net就可以在解码阶段逐步获得编码阶段丢失的微观信息,使得最后的输出同时包括微观信息与宏观信息。每一个像素点最终被分为哪一类,都可以同时兼顾其本身的信息,以及其周边小的区域、周边大的区域,甚至总体的宏观细心决定。其示意图如下:
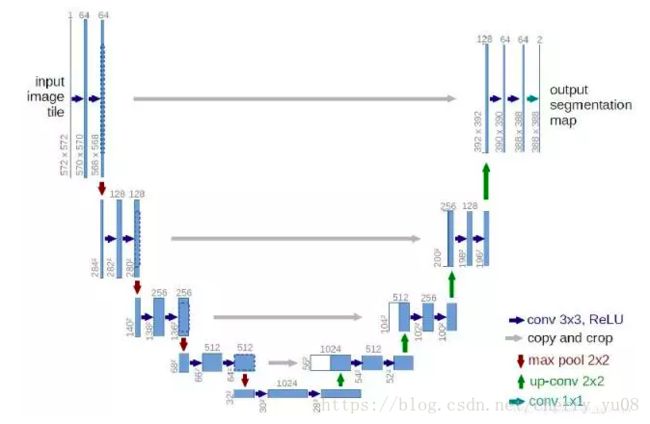
在Daniel M. Pelt与James A. Sethian的论文《A mixed-scale dense convolutional neural network for image analysis》中,也提出,可以将DenseNet的密集连接的思想运用于U-Net中,这样有利于多种尺度的信息高效传递,便于在U-Net各个层分别高效地提取出各个尺度的信息。其示意图如下: