斯坦福深度学习课程笔记(四)
卷积神经网络
- 历史
- 神经网络历史
- 视觉与卷积历史
- 现代应用
- 卷积和池化
- 视觉之外的神经网络
- Pooling 池化层
历史
ppt
神经网络历史
- 1957,感知机一代
- 1960,Adaline/Madaline ,尝试多层神经网络
- 1986,反向传播算法提出
- 2006,深度学习开始变得流行
Reinvigorated research in Deep Learning ,[Hinton and Salakhutdinov 2006]
- 2010-2012,深度网络在语音和视觉领域取得了突破
Acoustic Modeling using Deep Belief Networks(Abdel-rahman Mohamed, George Dahl, Geoffrey Hinton, 2010)
Context-Dependent Pre-trained Deep Neural Networks for Large Vocabulary Speech Recognition(George Dahl, Dong Yu, Li Deng, Alex Acero, 2012)
Imagenet classification with deep convolutional neural networks(Alex Krizhevsky, Ilya Sutskever, Geoffrey E Hinton, 2012)
视觉与卷积历史
- Topographical mapping in the cortex,皮质中的褶皱映射
- 视觉相关细胞的层次化结构
- 1980年,Fukushima应用细胞的层次化结构,提出了Neocognitron
- 1998年,LeCun等人提出了一个较小型的卷积网络,在邮政编码的识别上起到了很好的效果。Gradient-based learning applied to document recognition
- 2012年,ImageNet Classification with Deep Convolutional Neural Networks。alexNet提出,现代较流行的卷积网络结构
现代应用
现在卷积网络广泛用于物体分类、图像检索、侦测识别、自动驾驶、人脸识别、姿势识别、图像翻译、风格迁移等多个领域。
卷积和池化
在全连接层,我们是将一张图片拉伸一个长向量。比如我有一张 32 ∗ 32 ∗ 3 32*32*3 32∗32∗3的rgb图像,之前的神经网络模型会将其视为一个 3072 ∗ 1 3072*1 3072∗1的列向量,把此列向量作为输入 X X X,喂给神经网络模型。但是这样做破坏了图像本来的一个空间结构,遗失了图像的空间信息。
采用卷积层,能够更好地保留输入的空间结构。
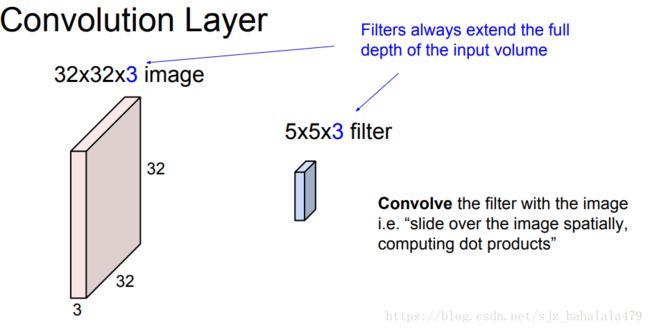
仍以一张 32 ∗ 32 ∗ 3 32*32*3 32∗32∗3的图像为例,我们给定一个卷积核(filter,或者叫过滤器、滤波器)。这个卷积核的宽和高一般比较小,但是它的色深和输入图像是相等的,这里设卷积核为 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3。
我们将卷积核从图片的左上角开始覆盖游走,每次覆盖时,将一一对应的卷积核像素点和图像的像素点相乘,再求和,得到一个新的值;然后游走,再覆盖,再求得一个点积值;直到将所有图片游走完,我们会得到很多值,这些值又可以构成一个新的层。
按上面那么说其实不太好理解,我们来举个实例。
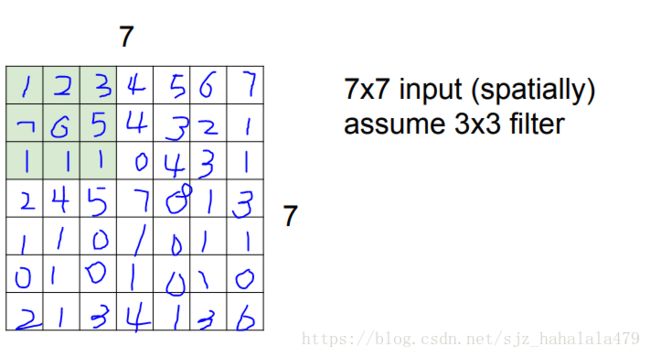
有一个 7 ∗ 7 7*7 7∗7的图像输入,上面每个像素点的值都是我瞎编的;我们还有一个卷积核:
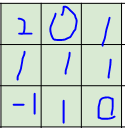
把这个卷积核覆盖到上面 7 ∗ 7 7*7 7∗7的图像中,从左上角开始,计算点积,结果应该是:
1 ∗ 2 + 2 ∗ 0 + 3 ∗ 1 + 7 ∗ 1 + 6 ∗ 1 + 5 ∗ 1 + 1 ∗ − 1 + 1 ∗ 1 + 1 ∗ 0 = 2 + 3 + 7 + 6 + 5 − 1 + 1 = 23 1*2+2*0+3*1+7*1+6*1+5*1+1*-1+1*1+1*0 = 2+3+7+6+5-1+1=23 1∗2+2∗0+3∗1+7∗1+6∗1+5∗1+1∗−1+1∗1+1∗0=2+3+7+6+5−1+1=23
然后,将卷积核向右游走(或者说移动)1个像素,再算一个点积;到头了之后从头再向下移动1个像素,一直算点积,最后,会的得到一个 5 ∗ 5 5*5 5∗5的矩阵,每一个元素值都是点积值。
当然,卷积核的大小,还有移动的步长,都是可以更改的,比如常用的卷积核大小还有 5 ∗ 5 5*5 5∗5, 7 ∗ 7 7*7 7∗7;步长可以是2个像素,或者三个像素。计算最终的输出维度有个公式:假设输入的图像长宽相等均为N,卷积核也是长宽相等均为F,步长为stride,最后输出的维度长和宽都是
N − F s t r i d e + 1 \frac{N-F}{stride} + 1 strideN−F+1
这里肯定会出现不整除的情况,我们可以通过在**图像边框填充全为0的像素(pad)**的方法来实现最终的整除。
说回到刚刚的 32 ∗ 32 ∗ 3 32*32*3 32∗32∗3的输入图像,我们有 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3的卷积核,最终输出的维度应为 28 ∗ 28 ∗ 1 28*28*1 28∗28∗1。实践中,卷积核不只一个,假设我们有6个刚刚维度的卷积核,最终输出的维度就是 28 ∗ 28 ∗ 6 28*28*6 28∗28∗6。
ConvNet是一系列卷积层,中间穿插着激活函数的网络。
之前提到可以用pad方法填充图像边缘,填充图像边缘还有一个好处,在于帮我们保持维度的统一性。因为我们输入的维度在正常的卷积处理后,会减小的很快,相应的丢失很多信息,通过pad使得每次卷积处理后输出的维度和输入一致,可以有效地缓解信息遗漏的问题。
一般来说,如何选择zero-padding的值呢?和卷积核的大小有关。设卷积核的大小为 F ∗ F F*F F∗F,那么zero-padding的值一般为
( F − 1 ) / 2 (F-1)/2 (F−1)/2
视觉之外的神经网络
如果我们从神经学/生物的视角解释卷积层,它大概就类似使用了局部连接的神经元;不关注全部输入,只关注图像空间的局部区域。
这里的filter卷积核也可以被称作receptive field感受野。
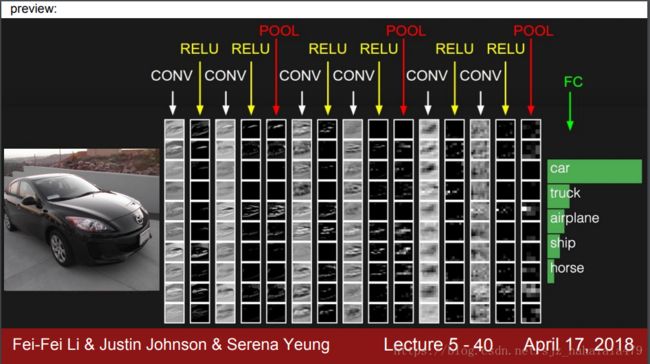
上一节有一个图,显示的是卷积神经网络的基本架构Conv+Relu+Pool+…+Dense,接下来讲一下Pooling池化层。
Pooling 池化层
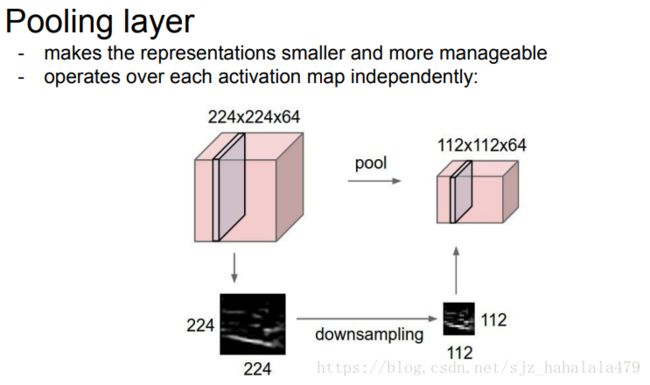
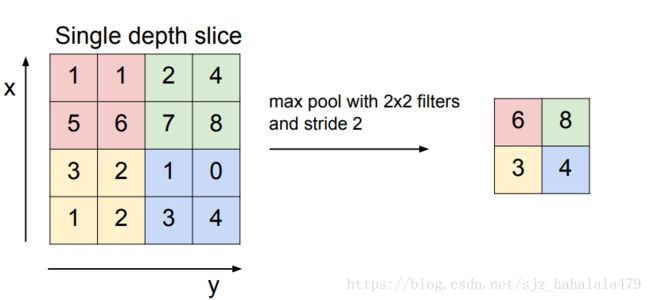
池化层相当于一个降采样,目的是减小输出的维度,比较常用的方法是max pooling最大池化层方法。
池化的方法和卷积很像,也是搞一个filter,然后在输入的那个大方阵中游走。图上的filter是 2 ∗ 2 2*2 2∗2的,步长为2。
总结这里和卷积层差不多,只不过池化层不需要padding了;而且池化层通常设置stride时不会使输入图像区域重叠。
由于卷积层中把stride设置大一些也是在做降采样,所以现在有去池化,只做卷积的趋势。
总结这里有很多值得注意的点
- CNN的经典结构是卷积层+池化层+最后的全连接层。
- 现在有使用更小的filter,和堆叠更深的层的趋势。
- 有去池化层/全连接层,只使用卷积层的趋势。
- 经典的CNN架构看起来是这样的:
[ ( C O N V − R E L U ) ∗ N − P O O L ? ] ∗ M − ( F C − R E L U ) ∗ K , S O F T M A X [(CONV-RELU)*N-POOL?]*M-(FC-RELU)*K,SOFTMAX [(CONV−RELU)∗N−POOL?]∗M−(FC−RELU)∗K,SOFTMAX
但是最近的网络不是采用这种方式。