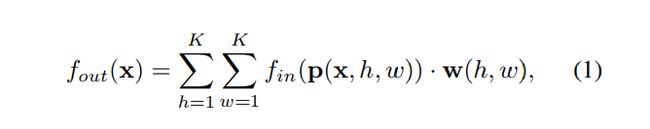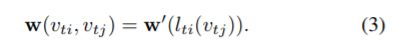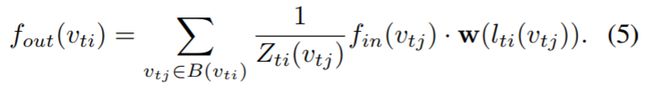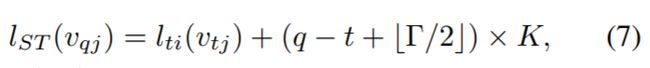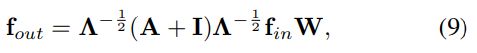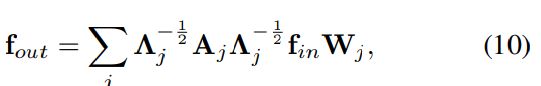ST-GCN时空图卷积网络
原文链接:https://arxiv.org/abs/1801.07455
3.1概述
基于骨架的的数据可以通过运动捕捉设备和姿态估计算法中获得。通常数据是序列帧,每一帧都有一组关节坐标。给出2D或者3D形式的序列化的坐标,我们就可以把关节作为节点,人体自然连接和时域连接做为边,构造一个时空图。ST-GCN的输入是图中的关节坐标向量。可以被认为是模仿基于2D图像的卷积网络,只不过2D图像有固定的像素格子。多层时空图卷积操作将应用于输入数据,并在graph上生成更高层次的特征图。然后被标准的SoftMax分类器分出动作类别。整个模型采用端到端的反向传播方式进行训练。现在我们将介绍ST-GCN模型中的组件。
3.2骨架图的构造
骨架序列通常由每帧中每个关节的二维或三维坐标来表示。先前的工作使用卷积进行骨架动作识别,Kim和Reiter连接所有关节的坐标向量,每帧形成一个单一的特征向量。在我们的工作中,我们利用时空图来形成骨架序列的层次表示。我们在N个节点和T帧的骨架序列上构造了一个无向空间时间图G=(V,E),该序列具有体内连接和帧间连接。
在这个图中,用V表示节点,V = {V ti ![]() | t = 1, . . . , T, i = 1, . . . , N},这其中包含了骨架序列中所有的节点。作为ST-GCN的输入,节点F(V ti
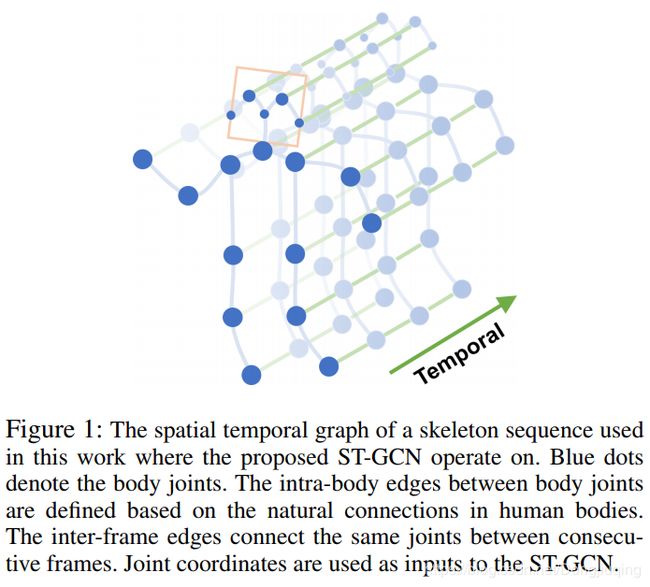
| t = 1, . . . , T, i = 1, . . . , N},这其中包含了骨架序列中所有的节点。作为ST-GCN的输入,节点F(V ti ![]() )上的特征向量包括帧t上第i节点的坐标向量和估计置信度。如图1所示,我们在骨架序列上分两步构造时空图。第一步,一帧内的所有关节根据人体结构的连通性用边缘连接,第二步,在连续帧中,每个关节点将连接到相同的关节点。因此这样设置的连接是自然定义的,无需手动分配部位。这也使网络体系结构能够处理具有不同关节数或关节连接数的数据集。例如,在Kinetics数据集上我们使用来自openpose的二维姿态估计结果,输出18个关节,而在Ntu-rgb+D数据集上我们使用三维关节跟踪结果作为输入,产生25个关节。ST-GCN可以在两种情况下运行,并提供一致的优越性能。所构造的时空图的示例如图1所示。
)上的特征向量包括帧t上第i节点的坐标向量和估计置信度。如图1所示,我们在骨架序列上分两步构造时空图。第一步,一帧内的所有关节根据人体结构的连通性用边缘连接,第二步,在连续帧中,每个关节点将连接到相同的关节点。因此这样设置的连接是自然定义的,无需手动分配部位。这也使网络体系结构能够处理具有不同关节数或关节连接数的数据集。例如,在Kinetics数据集上我们使用来自openpose的二维姿态估计结果,输出18个关节,而在Ntu-rgb+D数据集上我们使用三维关节跟踪结果作为输入,产生25个关节。ST-GCN可以在两种情况下运行,并提供一致的优越性能。所构造的时空图的示例如图1所示。
在形式上,边集E是由两个子集组成的,第一个子集描述了每帧内的骨架连接,表示为ES ![]() = {V ti V tj
= {V ti V tj ![]() | ( i,j) ∈ H},其中H是自然连接的人体关节集合。第二个子集包含帧间关节连接,它们将连续帧中相同的节点连接为EF
| ( i,j) ∈ H},其中H是自然连接的人体关节集合。第二个子集包含帧间关节连接,它们将连续帧中相同的节点连接为EF ![]() ={V ti V (t+1)i
={V ti V (t+1)i ![]() }。因此,对于EF
}。因此,对于EF ![]() 中一个特定的关节i的所有边,代表它随时间变化的轨迹。
中一个特定的关节i的所有边,代表它随时间变化的轨迹。
3.3空间图卷积神经网络
在我们深入到完整的ST-GCN之前,我们首先看一下在一个单帧内的CNN模型。在时间t帧,有N个关节点,表示为V t ![]() ,还有骨架边ES (t)
,还有骨架边ES (t)![]() = {V ti V tj
= {V ti V tj ![]() | ( i,j) ∈ H}, 回想二维图像或特征图上的卷积运算的定义,他们都可以看做是2D网格。卷积运算的输出特征图也是2D网格。通过步长1和适当的填充,输出特征图可以具有与输入特征图相同的大小。我们将在下面的讨论中假定步长1和适当填充,给出核大小为K×K的卷积算子和通道数c的输入特征映射F in
| ( i,j) ∈ H}, 回想二维图像或特征图上的卷积运算的定义,他们都可以看做是2D网格。卷积运算的输出特征图也是2D网格。通过步长1和适当的填充,输出特征图可以具有与输入特征图相同的大小。我们将在下面的讨论中假定步长1和适当填充,给出核大小为K×K的卷积算子和通道数c的输入特征映射F in ![]() 。在空间位置x上的单个通道的输出值可以写为
。在空间位置x上的单个通道的输出值可以写为
然后,通过将上面的公式扩展到输入特征图为空间图vt上,定义了对图的卷积运算。
采样函数。在图像上,采样函数p(h,w)根据中心位置x在相邻像素上定义。在图上,我们同样可以定义节点V ti ![]() 的邻域集B(V ti
的邻域集B(V ti ![]() )={ V tj
)={ V tj ![]() | d(V tj
| d(V tj ![]() ,V ti
,V ti![]() )≤D}上的采样函数。这里d(V tj
)≤D}上的采样函数。这里d(V tj ![]() ,V ti
,V ti![]() )表示从V tj
)表示从V tj![]() 到V ti
到V ti![]() 的最短路径。因此,采样函数p:B(V ti
的最短路径。因此,采样函数p:B(V ti![]() )→V可以编写为
)→V可以编写为
P (V ti![]() , V tj
, V tj![]() ) = V tj
) = V tj![]() (2)
(2)
在本工作中,我们对所有情况都使用D = 1,即连接范围为1的邻域集。较高的D是留给以后的工作。
-权重函数。与抽样函数相比,权重函数的定义更复杂。2D卷积中,中心位置附近存在确定性的网格,邻域内的像素就有固定的空间顺序。根据空间顺序对(c,K,K)维数的张量进行索引,可以实现权重函数。对于我们之前构造的graph来说,没有这样固定的排列,我们构建的权重函数,不是给每个相邻节点一个唯一的标签,而是通过将一个关节点V ti![]() 的邻集B(V ti
的邻集B(V ti![]() )划分为固定数量的K个子集来简化该过程,其中每个子集都有一个数字标签,加权函数通过索引(c,K)维度的向量来实现。3.4章节讨论分区策略。
)划分为固定数量的K个子集来简化该过程,其中每个子集都有一个数字标签,加权函数通过索引(c,K)维度的向量来实现。3.4章节讨论分区策略。
空间图卷积
利用改进的采样函数和权函数,重写Eq.1关于图的卷积形式:
其中的正则化项等于相应子集的基数,添加这一项可以平衡不同子集的贡献。我们用下面这个公式替代2/3/4三个公式
如果我们把图像看作一个规则的2D网格,这个公式可以类比标准的2D卷积。类比3×3卷积运算,以像素为中心的3×3网格中有一个9像素的邻域。然后,将相邻集划分为9个子集,每个子集具有一个像素。
时空建模
构造了空间图卷积网络之后,我们利用骨架序列对空间时间的动态进行建模。在时域方面,在连续帧之间连接同一关节点来构造graph,这使我们能够定义一个非常简单的策略,将空间图CNN扩展到时空域。也就是说,我们将邻域的概念扩展到包括时域连接的节点,如
参数Γ控制邻域图中包含的时间范围,因此可以称为时间内核大小。为了完成对时空图的卷积运算,还需要与空间相同的采样函数,以及权重函数,特别是标号图LST ![]() 由于时轴是有序的,所以我们直接修改了标签映射LST
由于时轴是有序的,所以我们直接修改了标签映射LST ![]() ,以使以Vti
,以使以Vti![]() 为根的空间时间邻域为
为根的空间时间邻域为
其中Lti![]() (Vtj
(Vtj![]() )是Vti
)是Vti![]() 中单个帧的标签映射。这样,我们在构造的时空图上有了一个定义良好的卷积运算.
中单个帧的标签映射。这样,我们在构造的时空图上有了一个定义良好的卷积运算.
3.4分区策略
设计一种划分策略实现标签映射L也非常重要。本文探索了几种分区策略,为简单叙述我们这几种分区策略,我们在单帧内讨论,因为他们可以自然的使用Eq.7拓展到时空域。
统一标签
最简单、最直接的分区策略是整个邻域集本身。在该策略中,每个相邻节点上的特征向量都有一个具有相同权重向量的内积。这一策略类有一个明显的缺点,即在单帧情况下,该策略等价于计算所有相邻节点的权重向量和平均特征向量之间的内积。对于骨架序列分类来说,这不是最优的,因为在这个操作中,局部的微分属性可能会丢失。形式上,我们有K=1和 Lti![]() (Vtj
(Vtj![]() ) = 0,∀I,j∈V。
) = 0,∀I,j∈V。
距离分割
另一种自然分区策略是根据节点到根节点Vti![]() 的距离d(·,Vti
的距离d(·,Vti![]() )对相邻集进行划分。在本文中,由于我们设置了D = 1,因此邻域集将被分成两个子集,其中d = 0表示根节点本身,其余的邻居节点位于d = 1子集中。因此,我们将有两个不同的权重向量,它们能够模拟局部微分性质,例如关节之间的相对平移。形式上,我们有K = 2和Lti
)对相邻集进行划分。在本文中,由于我们设置了D = 1,因此邻域集将被分成两个子集,其中d = 0表示根节点本身,其余的邻居节点位于d = 1子集中。因此,我们将有两个不同的权重向量,它们能够模拟局部微分性质,例如关节之间的相对平移。形式上,我们有K = 2和Lti![]() (Vtj
(Vtj![]() )=d(Vtj
)=d(Vtj![]() ,Vti
,Vti![]() )。
)。
空间配置分区
由于身体骨架是在空间上局域化的,我们可以在分区过程中利用这个特定的空间配置。设计了一种将领域节点划分为三个子集的策略:1)根节点本身;2)向心群:比根节点更靠近骨架重心的相邻节点;3)离心群。 在这里,骨架上所有关节的平均坐标为单帧骨架图的重心。这一策略的灵感来源于这样一个事实:人体各部分的运动大致可分为同心圆运动和偏心运动。形式上,我们表示如下:
其中ri![]() 是训练集中所有帧上从重心到关节i的平均距离。三种分区策略如图3所示。我们将对基于骨架的动作识别实验中提出的分区策略进行实证检验。预计更高级的分区策略将带来更好的建模能力和识别性能。
是训练集中所有帧上从重心到关节i的平均距离。三种分区策略如图3所示。我们将对基于骨架的动作识别实验中提出的分区策略进行实证检验。预计更高级的分区策略将带来更好的建模能力和识别性能。
3.5可学习边缘重要性加权
人们运动时关节会成群移动,一个关节可能出现在多个身体部位。然而,这些表现在建模这些动态部位时应该具有不同的重要性。从这个意义上讲,我们在时空图卷积的每一层上添加一个可学习的掩码M。该掩码M将根据ES![]() 中每个空间图形边缘的已知重要性权重,衡量(缩放)节点特征对相邻节点的贡献。经验表明,加入该掩码可以进一步提高ST-GCN的识别性能.也有可能有一个与数据相关的注意映射。我们把这个留给未来的工作。
中每个空间图形边缘的已知重要性权重,衡量(缩放)节点特征对相邻节点的贡献。经验表明,加入该掩码可以进一步提高ST-GCN的识别性能.也有可能有一个与数据相关的注意映射。我们把这个留给未来的工作。
3.6实现ST-GCN
我们采用类似于(Kipf和Wling 2017)对图卷积的实现,单视频帧内节点的体内连接由邻接矩阵A和单位矩阵I表示。
在单帧情况下,具有第一个分区策略的ST-GCN可以使用以下公式表示(Kipf和Wling 2017)。
whereΛ ii=![]() j(Aij+Iij)
j(Aij+Iij)![]() , Λ ii
, Λ ii![]() 是对角线元素,对角线的元素等于第i行所有元素之和+1 。多个输出通道权重向量堆叠成权重矩阵W,在时空域中,我们将输入的特征图表示为(C,V,T)维度的张量,图卷积是通过执行1 × Γ标准的二维卷积来实现的,并乘以第二维上用归一化邻接矩阵
是对角线元素,对角线的元素等于第i行所有元素之和+1 。多个输出通道权重向量堆叠成权重矩阵W,在时空域中,我们将输入的特征图表示为(C,V,T)维度的张量,图卷积是通过执行1 × Γ标准的二维卷积来实现的,并乘以第二维上用归一化邻接矩阵![]() 得到的张量。
得到的张量。
对于多子集的分区策略,距离分割和空间配置分割,我们要再次利用上述的实现方式,需要注意点是,现在的邻接矩阵被分解为几个矩阵Aj![]() ,其中A+I=∑j(Aj)
,其中A+I=∑j(Aj)![]() ,例如,在距离分区策略中,A0=I,A1
,例如,在距离分区策略中,A0=I,A1![]() = A,公式9转化为公式10.
= A,公式9转化为公式10.
类似的Λjii![]() =∑k(Ajik)
=∑k(Ajik)![]() +α,设置α=0.001 以避免Aj
+α,设置α=0.001 以避免Aj![]() 空行。
空行。
实现可学习的边缘重要性加权是很简单的。对于每个邻接矩阵,我们伴随着一个可学习的权重矩阵M。我们分别用(A+I)⊗M和Aj![]() ⊗M代替了Eq.9的矩阵A+I和Eq.10中的Aj
⊗M代替了Eq.9的矩阵A+I和Eq.10中的Aj![]() 。这里⊗表示两个矩阵之间的元素乘积。掩码M被初始化为一个全一矩阵.
。这里⊗表示两个矩阵之间的元素乘积。掩码M被初始化为一个全一矩阵.
网络架构和训练
ST-GCN在不同的节点上共享权重,在不同的节点上保持输入数据的规模一致很重要。实验中,首先将骨架输入到一个批处理归一化(BN)层,以实现数据的规范化。ST-GCN模型由9层时空图卷积算子(ST-GCN单元)组成.前三层有64个输出通道,之后三个层有128个输出通道,最后三层有256个输出通道。这些层有9个时间内核大小。Resnet机制应用于每个ST-GCN单元。在每个ST-GCN单元后,我们以0.5的概率随机dropout每个STGCN单元的特征,以避免过拟合。第4、第7层的时域卷积层的步长设置为2作为池化层,之后对得到的张量进行全局池化运算,得到每个序列的256维特征向量,最后,我们将它们提供给一个SoftMax分类器。模型采用随机梯度下降学习,学习率为0.01。每隔10个Epoch,我们的学习率就会下降0.1。为了避免过度拟合,在对Kinetics数据集进行训练时,我们进行了两种增强,以代替Dropout层。首先,为了模拟摄像机的运动,我们对所有帧的骨架序列进行随机仿射变换。我们选取了几个固定的角度、平移和缩放三种因素作为候选,然后随机抽取三个因素的两个组合来产生仿射变换。这种转换被内插到中间帧以产生效果,就像我们在回放期间平稳地移动视角一样。我们把这种增强称为随机移动。第二,在训练中随机抽取原始骨架序列中的片段,并使用测试中的所有帧。网络顶部的全局池使网络能够处理长度不确定的输入序列。
4数据集
Kinetics包含从YouTube上检索到的大约30万段视频片段。视频涵盖了多达400个人类动作,从日常活动,体育场景,到复杂的行动与互动。Kinetics中的每一个片段大约持续10秒。此Kinetics数据集仅提供原始视频剪辑,不提供骨架数据。在本文中,我们将重点放在基于骨架的动作识别上,因此我们使用像素坐标系中估计的关节位置作为输入,并丢弃原始的RGB帧。为了获得关节位置,我们首先将所有视频的大小调整为340×256,并将帧速率转换为30 FPS。之后我们使用了openpose方法,估计每一帧中18个关键点位置。这个方法会出18个关键点2D坐标和置信度(X,Y,C),因此,我们用一个元组(X,Y,C)表示每个关节,并将一个骨架帧记录为一个由18个元组成的数组。对于多人的情况,选取中平均最高置信度的两个人。这样,一个带有T帧的剪辑被转换成这些元组的骨架序列。在实践中,我们用(3,T,18,2)维张量来表示一个剪辑。为了简单起见,我们从一开始就通过重放序列来填充每一个剪辑,使T=300。我们将发布Kinetics关节位置的再现结果。我们按照数据集作者的建议,用TOP-1和TOP-5来评估识别性能(Kay等人)。2017年)。数据集提供了240,000个剪辑的训练集和20,000个验证集。我们在训练集上训练模型,并在验证集上报告准确性。
NTU-RGB+D
NTU-RGB+D是目前最大的3D行为识别数据集,包括了56000个动作剪辑,60种动作。这些剪辑都是由40名志愿者在一个受限的实验室环境中拍摄的,并同时记录了三个摄像机视图。所提供的注释给出了由Kinect深度传感器检测到的摄像机坐标系中的三维关节位置(X、Y、Z)。在骨架序列中,每个主体有25个关节。每个剪辑保证最多有两个主题。
该数据集的作者推荐了两个基准:
- 交叉主题(X-Sub)基准: 用40320个剪辑训练和16560个剪辑用来验证。在这种情况下,训练片段来自演员的一个子集,模型根据演员其余的片段进行评估;
- 横视(X-View)基准: 用37920个剪辑训练和18960个剪辑验证。此设置中的训练剪辑来自摄像机2和3视角,评估剪辑全部来自摄像机1视角。我们遵循这一惯例,并在这两个基准上报告最高1的识别精度。
4.2对比学习
时空图卷积 :首先,我们评估了使用时空图卷积运算的必要性。我们使用了一个基线网络体系结构(Kim和Reiter,2017),其中所有的空间时间卷积都被时间卷积所取代。也就是说,我们连接所有的输入节点位置,以形成输入特征在每个帧t。然后,时间卷积将对这个输入进行操作,并随着时间的推移而旋转。我们称此模型为“基线tcn”。
这种识别模型在约束数据集(如NTU-RGB+D)上工作得很好。从表1中可以看出,具有空间时间图卷积的模型,具有合理的分区策略,在动力学方面始终优于基线模型。实际上,这种时间卷积等价于在完全连通的联合图上具有不可共享权的空间时态图卷积。
因此,基线模型与ST-GCN模型的主要区别在于卷积运算中的稀疏自然连接和共享权。此外,我们还评估了基线模型和ST-GCN之间的一个中间模型,称为“局部卷积”。在该模型中,我们使用稀疏联合图作为ST-GCN,而使用不共享权值的卷积滤波器。我们相信,基于st-gcn的模型的较好的性能可以证明时空图卷积在基于骨架的动作识别中的作用